La început, este de obicei necesar să ne facem o idee despre diagrama pV a ciclului. Pentru aceasta vom trasa curbele proceselor izocoric și adiabatic. Graficul aproximativ al ciclului Otto este prezentat în figura următoare.

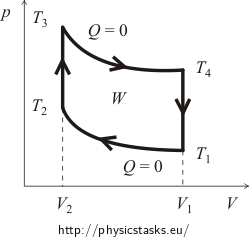
Eficiența η a ciclului se definește ca

\

unde W este lucrul efectuat de gaz în timpul unui ciclu minus lucrul efectuat de forțele exterioare (în diagramă este reprezentat de suprafața ariei definite de liniile ciclului!), iar Qsup este căldura furnizată sistemului în timpul ciclului.

Lucrul W poate fi calculat folosind relația dintre presiune și volum în timpul unei dilatări și comprimări adiabatice (lucrul efectuat în timpul unui proces izocoric este, desigur, zero). În această sarcină, însă, va fi mai bine să folosim faptul că variația totală a energiei interne pe ciclu trebuie să fie egală cu zero (ne întoarcem la aceeași stare ca la început, deci temperatura și, prin urmare, energia internă rămân aceleași!) În conformitate cu prima lege a termodinamicii, lucrul efectuat de gaz poate fi exprimat ca diferența dintre căldura Qsup furnizată și căldura Qrel eliberată. Formula pentru randamentul ciclului este, prin urmare, de forma

\

În primul rând, vom calcula căldura furnizată Qsup. Este clar că în timpul procesului adiabatic nu există schimb de căldură, iar în timpul răcirii izocorice căldura este eliberată. Aceasta înseamnă că căldura va fi furnizată numai în timpul încălzirii izocorice de la temperatura T2 la temperatura T3. Cantitatea acestei călduri poate fi exprimată în variabilele cantității de substanță n a gazului și a capacității sale termice molare CV după cum urmează:

\

Vom exprima cantitatea de căldură degajată Qrel cam în același mod. Știm deja că căldura este degajată numai în timpul răcirii izocorice de la temperatura T4 înapoi la temperatura inițială T1. Este adevărat că:

\

Acum înlocuim aceste formule în formula randamentului ciclului și obținem imediat:

\ \

Acum va trebui să exprimăm diferențele de temperatură folosind raportul de compresie dat

\

și raportul lui Poisson κ.

Pentru a face acest lucru, vom folosi ecuația pentru un gaz ideal supus unui proces adiabatic (legea lui Poisson) pVκ = C = konst.., unde C este o constantă. Acum evaluăm presiunea din ecuația de stare a unui gaz ideal

\

pe care o înlocuim în legea lui Poisson. Acum transferăm constantele (C și K) într-o parte

\

Acum aplicăm această lege a lui Poisson pentru ambele procese adiabatice. Pentru expansiunea adiabatică obținem relația

\

Și pentru compresia adiabatică obținem

\

Acum scădem a doua ecuație din prima și factorizăm V1κ – 1 pe de o parte și V2κ – 1 pe de altă parte. Obținem:

\\ \

Vezi că am reușit de fapt să exprimăm diferențele de temperatură folosind valorile date. Acum înlocuim această relație în formula pentru randament și obținem ecuația finală:

\\ \ \