Grafy v Pythonu

Původ teorie grafů

Než se pustíme do vlastní implementace grafů v Pythonu a než začneme s představováním modulů Pythonu zabývajících se grafy, chceme se věnovat počátkům teorie grafů.
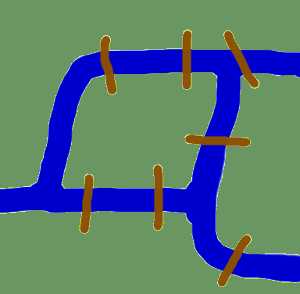
Počátky nás zavedou v čase do Künigsbergu 18. století. Königsberg byl tehdy městem v Prusku. Městem protékala řeka Pregel a vytvářela dva ostrovy. Město a ostrovy spojovalo sedm mostů, jak je znázorněno na obrázku. Obyvatele města dojímala otázka, zda je možné projít se městem tak, že navštívíme každou jeho část a každý most přejdeme jen jednou? Každý most musel být přejit celý, tj. není dovoleno přejít polovinu mostu a pak se otočit a později přejít druhou polovinu z druhé strany. Procházka nemusí začínat a končit na stejném místě. tento problém vyřešil v roce 1735 Leonhard Euler, který dokázal, že to není možné. Zjistil, že volba trasy uvnitř jednotlivých pozemků je irelevantní a že záleží pouze na pořadí (neboli sekvenci), v jakém se mosty přechází. Zformuloval abstrakci problému, odstranil nepotřebná fakta a soustředil se na pozemní oblasti a mosty, které je spojují. Vytvořil tak základy teorie grafů. Pokud se na “pozemní oblast” díváme jako na vrchol a na každý most jako na hranu, “zredukovali” jsme problém na graf.

Úvod do teorie grafů pomocí jazyka Python

Než se pustíme do pojednání o možných reprezentacích grafů v jazyce Python, chceme uvést několik obecných definic grafů a jejich složek.
“Graf “1 se v matematice a informatice skládá z “uzlů”, známých také jako “vrcholy”.2 Uzly mohou, ale nemusí být vzájemně propojeny. Na našem obrázku, který je obrazovým znázorněním grafu, je uzel “a” spojen s uzlem “c”, ale “a” není spojen s “b”. Spojnice mezi dvěma uzly se nazývá hrana. Pokud jsou hrany mezi uzly neorientované, nazývá se graf neorientovaný graf. Pokud je hrana směrovaná z jednoho vrcholu (uzlu) do druhého, nazývá se graf směrovaný graf. Směrovaná hrana se nazývá oblouk.
Ačkoli grafy mohou vypadat velmi teoreticky, mnoho praktických problémů lze znázornit pomocí grafů. Často se používají k modelování problémů nebo situací ve fyzice, biologii, psychologii a především v informatice. V informatice se grafy používají k reprezentaci komunikačních sítí, organizace dat, výpočetních zařízení, toku výpočtů,
v posledním případě se používají k reprezentaci organizace dat, jako je souborový systém operačního systému, nebo komunikačních sítí. Na strukturu odkazů webových stránek lze také pohlížet jako na graf, tj. směrovaný graf, protože odkaz je směrovaná hrana nebo oblouk.

Python nemá žádný vestavěný datový typ nebo třídu pro grafy, ale je snadné je v Pythonu implementovat. Jeden datový typ je pro reprezentaci grafů v jazyce Python ideální, a to slovníky. Graf na našem obrázku lze implementovat následujícím způsobem:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Klíče výše uvedeného slovníku jsou uzly našeho grafu. Odpovídající hodnoty jsou seznamy s uzly, které jsou spojeny hranou. Neexistuje jednodušší a elegantnější způsob reprezentace grafu.
Na hranu se můžeme dívat jako na 2-tuple s uzly jako prvky, tedy (“a”, “b”)
Funkce pro generování seznamu všech hran:Tento kód generuje následující výstup, pokud je kombinován s dříve definovaným slovníkem grafu:

 $ python3 graph_simple.py 

Jak vidíme, neexistuje žádná hrana obsahující uzel “f”. “f” je izolovaný uzel našeho grafu.
Následující funkce Pythonu vypočítá izolované uzly daného grafu:Zavoláme-li tuto funkci s naším grafem, vrátí se seznam obsahující “f”:

Graf jako třída jazyka Python

Než budeme pokračovat v psaní funkcí pro grafy, vyzkoušíme si poprvé implementaci třídy grafů v jazyce Python. Pokud se podíváte na následující výpis naší třídy, uvidíte, že v metodě __init__ používáme slovník “self.__graph_dict” pro ukládání vrcholů a jim odpovídajících sousedních vrcholů.
Pokud tento modul spustíte samostatně, dostanete následující výsledek:

Cesty v grafech

Chceme nyní najít nejkratší cestu z jednoho uzlu do jiného uzlu. Než přejdeme ke kódu Pythonu pro tento problém, budeme muset uvést několik formálních definic.
Sousední vrcholy:
Dva vrcholy jsou sousední, když oba mají společnou hranu.
Cesta v neorientovaném grafu:
Cesta v neorientovaném grafu je posloupnost vrcholů P = ( v1, v2, …., vn ) ∈ V x V x … x V taková, že vi sousedí s v{i+1} pro 1 ≤ i < n. Taková cesta P se nazývá cesta délky n z v1 do vn.
Jednoduchá cesta:
Cesta bez opakujících se vrcholů se nazývá jednoduchá cesta.
Příklad:
(a, c, e) je jednoduchá cesta v našem grafu, stejně jako (a,c,e,b). (a,c,e,b,c,d) je cesta, ale není to jednoduchá cesta, protože vrchol c se vyskytuje dvakrát.
Následující metoda najde cestu z počátečního vrcholu do koncového vrcholu:Pokud uložíme naši třídu grafu včetně metody find_path jako “graphs.py”, můžeme si ověřit způsob práce naší funkce find_path:Výsledek předchozího programu vypadá takto:
Metoda find_all_paths najde všechny cesty mezi počátečním vrcholem a koncovým vrcholem:Náš příklad grafu jsme mírně pozměnili přidáním hran z “a” do “f” a z “f” do “d”, abychom otestovali dříve definovanou metodu:Výsledek vypadá takto:

Stupeň

Stupeň vrcholu v v grafu je počet hran, které ho spojují, přičemž smyčky se počítají dvakrát. Stupeň vrcholu v se označuje deg(v). Maximální stupeň grafu G, označovaný Δ(G), a minimální stupeň grafu, označovaný δ(G), jsou maximální a minimální stupně jeho vrcholů.
V grafu na pravé straně je maximální stupeň 5 ve vrcholu c a minimální stupeň je 0, tj. izolovaný vrchol f.
Jsou-li všechny stupně v grafu stejné, jedná se o regulární graf. v regulárním grafu jsou všechny stupně stejné, a proto můžeme mluvit o stupni grafu.
Formule pro součet stupňů (Handshakingovo lemma):
∑v &in; Vdeg(v) = 2 |E|
To znamená, že součet stupňů všech vrcholů je roven počtu hran vynásobenému číslem 2. Z toho můžeme vyvodit, že počet vrcholů s lichým stupněm musí být sudý. Toto tvrzení je známé jako lemma o chvění rukou. Název “handshaking lemma” vychází z populární matematické úlohy: V libovolné skupině lidí je počet lidí, kteří si podali ruku s lichým počtem jiných lidí ze skupiny, sudý.
Následující metoda vypočítá stupeň vrcholu:
Následující metoda vypočítá seznam obsahující izolované vrcholy grafu:Metody delta a Delta lze použít k výpočtu minimálního, resp. maximálního stupně vrcholu:

Posloupnost stupňů

Posloupnost stupňů neorientovaného grafu je definována jako posloupnost stupňů jeho vrcholů v nerostoucím pořadí.
Následující metoda vrací tuple s posloupností stupňů instančního grafu:
Stupňová posloupnost našeho příkladového grafu je následující posloupnost celých čísel: (5,2,1,1,1,0).
Izomorfní grafy mají stejnou posloupnost stupňů. Dva grafy se stejnou posloupností stupňů však nemusí být nutně izomorfní.
Je otázka, zda lze danou posloupnost stupňů realizovat jakojednoduchý graf. Erdösova-Gallaiova věta říká, že nerostoucí posloupnost n čísel di (proi = 1, …., n) je posloupností stupňů jednoduchého grafu tehdy a jen tehdy, je-li součet této posloupnosti sudý a je-li splněna následující podmínka:

Implementace Erdösovy-Gallaiovy věty

Naše třída grafů – kompletní výpis viz dále – obsahuje metodu “erdoes_gallai”, která rozhoduje, zda posloupnost splňuje Erdösovu-Gallaiovu větu. Nejprve zkontrolujeme, zda je součet prvků posloupnosti lichý. Pokud ano, funkce vrátí False, protože Erdös-Gallaiova věta již nemůže být splněna. Poté pomocí statické metody is_degree_sequence ověříme, zda je vstupní posloupnost stupňová, tj. zda jsou prvky posloupnosti nerostoucí. To je trochu zbytečné, protože se předpokládá, že vstup je posloupnost stupňů, takže tuto kontrolu můžete kvůli efektivitě vypustit. Nyní v těle druhého příkazu if zkontrolujeme, zda je splněna nerovnice věty:

Verze bez testu zbytečné posloupnosti stupňů:

Hustota grafu

Hustota grafu je definována jako poměr počtu hran daného grafu a celkového počtu hran, které by graf mohl mít. Jinými slovy: Měří, jak blízko je daný graf úplnému grafu.
Maximální hustota je 1, pokud je graf úplný. To je jasné, protože maximální počet hran v grafu závisí na vrcholech a lze jej vypočítat takto:
max. počet hran = ½ * |V| * ( |V| – 1 ).
Naopak minimální hustota je 0, pokud graf nemá žádné hrany, tj. jedná se o izolovaný graf.
Pro neorientované jednoduché grafy je hustota grafu definována takto: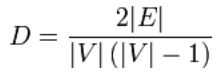

Hustý graf je graf, v němž se počet hran blíží maximálnímu počtu hran. Graf, který má jen několik málo hran, se nazývá řídký graf. Definice těchto dvou pojmů není příliš ostrá, tj. neexistuje žádná nejmenší horní hranice (supremum) pro řídký hustý graf a žádná největší dolní hranice (infimum) pro definování hustého grafu.
Nejpřesnější matematický zápis používá notaci velkého O:
Rídký graf:
Hustý graf:
Hustý graf je graf G = (V, E), ve kterém |E| = Θ(|V|2).
“density” je metoda naší třídy pro výpočet hustoty grafu:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Tuto metodu můžeme otestovat pomocí následujícího skriptu. Úplný graf má hustotu 1 a izolovaný graf má hustotu 0, jak vidíme z výsledků předchozího testovacího skriptu:

$ python test_density.py 0.4666666666671.00.0

Spojité grafy

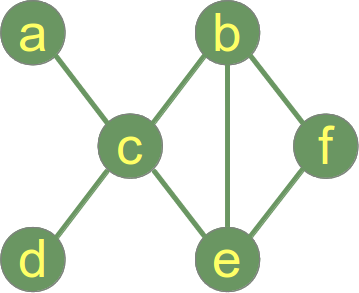O grafu se říká, že je spojitý, pokud je každá dvojice vrcholů v grafu spojitá. Příkladový graf na pravé straně je spojitý graf.
Jednoduchým algoritmem lze určit, zda je graf spojitý:

1. Zvolte libovolný uzel x grafu G jako výchozí bod
2. Určete množinu A všech uzlů, do kterých lze z x dojít.
3. Jestliže se A rovná množině uzlů grafu G, je graf spojitý, jinak je nespojitý.

Implementujeme metodu is_connected pro kontrolu, zda je graf spojitý. Neklademe důraz na efektivitu, ale na čitelnost.
Přidáme-li tuto metodu do naší třídy grafů, můžeme ji otestovat následujícím skriptem. Za předpokladu, že třídu grafů uložíte jako graph2.py:
Spojitá komponenta je maximálně spojitý podgraf grafu G. Každý vrchol patří přesně do jedné spojené komponenty, stejně jako každá hrana.

Vzdálenost a průměr grafu

Vzdálenost “dist” mezi dvěma vrcholy grafu je délka nejkratší cesty mezi těmito vrcholy. Při výpočtu vzdálenosti nejsou povoleny žádné zpětné kroky, okliky ani smyčky.
V našem příkladovém grafu vpravo je vzdálenost mezi vrcholem a a vrcholem f 3, tj. dist(a,f) = 3, protože nejkratší cesta vede přes vrcholy c a e (nebo alternativně c a b).

Excentricita vrcholu s grafu g je maximální vzdálenost ke každému jinému vrcholu grafu:
e(s) = max( { dist(s,v) | v ∈ V })
(V je množina všech vrcholů grafu g)
Průměr d grafu je definován jako maximální excentricita libovolného vrcholu v grafu. To znamená, že průměr je délka nejkratší cesty mezi nejvzdálenějšími vrcholy. Chcete-li určit průměr grafu, najděte nejprve nejkratší cestu mezi každou dvojicí vrcholů. Největší délka kterékoli z těchto cest je průměrem grafu.
V našem příkladovém grafu přímo vidíme, že průměr je 3, protože minimální délka mezi a a f je 3 a neexistuje žádná jiná dvojice vrcholů s delší cestou.
Následující metoda implementuje algoritmus pro výpočet průměru. Průměr našeho příkladového grafu můžeme vypočítat pomocí následujícího skriptu, opět za předpokladu, že je naše kompletní třída grafu uložena jako graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Vypíše hodnotu 3.

Kompletní třída grafu Pythonu

V následujícím kódu Pythonu najdete kompletní modul třídy Pythonu se všemi diskutovanými metodami:graph2.py

Strom / les

Strom je neorientovaný graf, který neobsahuje žádné cykly. To znamená, že libovolné dva vrcholy grafu jsou spojeny právě jednou jednoduchou cestou.
Les je nesouvislé spojení stromů. Na rozdíl od lesů v přírodě se les v teorii grafů může skládat z jediného stromu!!!
Stromem (a lesem) je graf s jedním vrcholem a bez hrany.
Příklad stromu: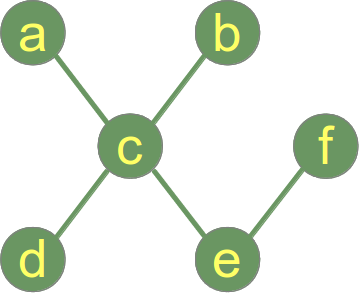

Předchozí příklad znázorňuje graf, který je stromem a lesem, následující obrázek ukazuje graf, který se skládá ze dvou stromů, tj. stromů.Tj. graf je lesem, ale není stromem:

Přehled lesů:

S jedním vrcholem:

Graf lesa se dvěma vrcholy:

Lesové grafy se třemi vrcholy:

Strom rozpětí

Strom rozpětí T spojitého neorientovaného grafu G je podgraf G’ grafu G, který je stromem,a G’ obsahuje všechny vrcholy a podmnožinu hran grafu G. G’ obsahuje všechny hrany grafu G, pokud je G stromový graf. Neformálně je rozpínací strom G výběr hran G, které tvoří strom procházející každým vrcholem. To znamená, že každý vrchol leží ve stromu, ale neobsahuje žádné cykly (nebo smyčky).
Příklad:
Plně spojitý graf: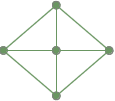

Dva rozpínací stromy z předchozího plně spojitého grafu: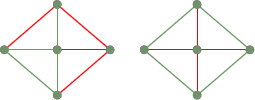

Hamiltonova hra

Hamiltonova cesta je cesta v neorientovaném nebo orientovaném grafu, která navštíví každý vrchol přesně jednou. Hamiltonovský cyklus (nebo okruh) je hamiltonovská cesta, která je cyklem.
Poznámka pro informatiky: Obecně není možné určit, zda takové cesty nebo cykly existují v libovolných grafech, protože bylo prokázáno, že problém hamiltonovské cesty je NP-úplný.
Je pojmenován po Williamu Rowanu Hamiltonovi, který vymyslel takzvanou “ikosovou hru” neboli Hamiltonův hlavolam, který spočívá v nalezení hamiltonovského cyklu v hranovém grafu dodekaedru. Hamilton tento problém vyřešil pomocí ikosového kalkulu, algebraické struktury založené na kořenech jednoty s mnoha podobnostmi s kvaterniony, které rovněž vynalezl.

Úplný výpis třídy Graph

Tuto třídu Graph můžeme otestovat pomocí následujícího programu:Spustíme-li tento program, dostaneme následující výstup:
Poznámky:
1 Grafy studované v teorii grafů (a v této kapitole našeho výukového programu Python) bychom neměli zaměňovat s grafy funkcí
2 Singleton je množina, která obsahuje právě jeden prvek.
Kreditky:
Narayana Chikkam, nchikkam(at)gmail(dot)com, upozornil na chybu indexu v metodě “erdoes_gallai”. Moc děkuji, Narayano!