Kolmogorov-Smirnovův test
K-S test je test shody, který se používá k posouzení rovnoměrnosti rozdělení souboru dat. Byl navržen jako reakce na nedostatky chí-kvadrát testu, který poskytuje přesné výsledky pouze pro diskrétní, binované rozdělení. Výhodou K-S testu je, že nepředpokládá binování porovnávaných souborů dat, čímž odstraňuje libovolnost a ztrátu informací, které proces výběru binů provázejí.
Ve statistice je K-S test uznávaným testem pro měření rozdílů mezi spojitými soubory dat (rozděleními dat bez binování), které jsou funkcí jedné proměnné. Tato míra rozdílu, statistika K-S \(D\), je definována jako maximální hodnota absolutního rozdílu mezi dvěma kumulativními distribučními funkcemi. Jednostranný K-S test se používá k porovnání souboru dat se známou kumulativní distribuční funkcí, zatímco oboustranný K-S test porovnává dva různé soubory dat. Každý soubor dat poskytuje jinou kumulativní distribuční funkci a její význam spočívá v jejím vztahu k pravděpodobnostnímu rozdělení, z něhož je soubor dat vybrán: pravděpodobnostní distribuční funkce pro jednu nezávislou proměnnou \(x\) je funkce, která každé hodnotě \(x\) přiřazuje určitou pravděpodobnost. Pravděpodobnost, kterou předpokládá konkrétní hodnota \(x_{i}\), je hodnota distribuční funkce pravděpodobnosti při \(x_{i}\) a označuje se \(P(x_{i})\).Kumulativní distribuční funkce je definována jako funkce udávající podíl datových bodů nalevo od dané hodnoty \(x_{i}\), \(P(x <x_{i})\); představuje pravděpodobnost, že \(x\) je menší nebo rovna určité hodnotě \(x_{i}\).
Pro porovnání dvou různých kumulativních distribučních funkcí \(S_{N1}(x)\) a \(S_{N2}(x)\) je tedy K-S statistika
D = max|S_N1(x) – S_N2(x)|
kde \(S_{N}(x)\) je kumulativní distribuční funkce pravděpodobnostního rozdělení, ze kterého je vybrán soubor dat s \(N\) událostí. Pokud se \(N\) uspořádané události nacházejí v datových bodech \(x_{i}\), kde \(i = 1, \ldots, N\), pak
S_N(x_i) = (i-N)/N
, kde je pole dat \(x\) uspořádáno vzestupně. Jedná se o skokovou funkci, která se zvyšuje o \(1/N\) při hodnotě každého uspořádaného datového bodu.
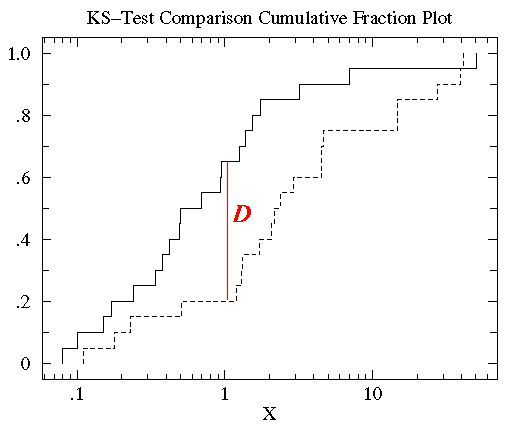
Kirkman, T.W. (1996) Statistici k použití.
http://www.physics.csbsju.edu/stats/
Pro naše účely se porovnávají dvě rozdělení: naměřené rozdělení časů příchodů a kumulovaný podíl na uplynulém časovém intervalu. Pokud platí nulová hypotéza (žádná variabilita), dostaneme 50 % vašich událostí v 50 % uplynulého času a statistika \(D\) by se měla rozdělit podle Kolmogorovova rozdělení pro mnoho realizací rozdělení časů příchodů. Pravděpodobnost vrácená testem je tedy \(p_{KS} = 1 – \alfa\), kde \(\alfa\) je pravděpodobnost (podle Kolmogorovova rozdělení), že hodnota \(D\) je větší nebo rovna naměřené hodnotě. Malá hodnota \(p_{KS}\) tedy naznačuje shodu s nulovou hypotézou, zatímco velká hodnota \(p_{KS}\) naznačuje, že interval mezi událostmi není konstantní, a proto lze usuzovat na variabilitu.