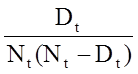Existuje několik různých způsobů odhadu funkce přežití nebo křivky přežití. Existuje řada populárních parametrických metod, které se používají k modelování údajů o přežití, a liší se předpoklady, které jsou učiněny o rozdělení dob přežití v populaci. Mezi oblíbená rozdělení patří exponenciální, Weibullovo, Gompertzovo a logaritmicko-normální rozdělení.2 Pravděpodobně nejoblíbenější je exponenciální rozdělení, které předpokládá, že pravděpodobnost, že účastník utrpí událost, která ho zajímá, je nezávislá na tom, jak dlouho je tato osoba bez události. Ostatní rozdělení vytvářejí různé předpoklady o pravděpodobnosti vzniku události u jedince (tj. může se zvyšovat, snižovat nebo měnit v čase). Podrobnější informace o parametrických metodách analýzy přežití lze nalézt v publikacích Hosmer a Lemeshow a Lee a Wang1,3.

Na tomto místě se zaměříme na dvě neparametrické metody, které nevytvářejí žádné předpoklady o tom, jak se pravděpodobnost vzniku události u dané osoby mění v čase. Pomocí neparametrických metod odhadujeme a vykreslujeme rozdělení přežití nebo křivku přežití. Křivky přežití se často vykreslují jako skokové funkce, jak je znázorněno na obrázku níže. Na ose X je znázorněn čas a na ose Y přežití (podíl ohrožených osob). Všimněte si, že procento přeživších účastníků nepředstavuje vždy procento žijících (což předpokládá, že výsledkem zájmu je smrt). “Přežití” může také znamenat podíl těch, kteří jsou bez jiné výsledné události (např. procento bez infarktu myokardu nebo kardiovaskulárního onemocnění), nebo může také představovat procento těch, u kterých nedošlo ke zdravému výsledku (např. remise rakoviny).

Funkce přežití

Všimněte si, že po dobu 2 let je pravděpodobnost přežití 100 % a poté klesá na 90 %. Medián přežití je 9 let (tj. 50 % populace přežije 9 let; viz čárkované čáry).

Příklad:

Uvažujte o malé prospektivní kohortové studii určené ke studiu doby do smrti. Studie zahrnuje 20 účastníků ve věku 65 let a starších; jsou zařazeni do studie po dobu 5 let a jsou sledováni po dobu až 24 let, dokud nezemřou, studie neskončí nebo dokud ze studie nevypadnou (ztratí se ze sledování). Údaje jsou uvedeny níže. Ve studii je 6 úmrtí a 3 účastníci s úplným sledováním (tj. 24 let). Zbývajících 11 účastníků má méně než 24 let sledování z důvodu pozdního zařazení do studie nebo ztráty ze sledování.

Identifikační číslo účastníka	Rok úmrtí	Rok. posledního kontaktu
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

Životní tabulka (pojistně-matematická tabulka)

Jedním ze způsobů shrnutí zkušeností účastníků je životní tabulka, nebo pojistně-matematickou tabulkou. Životní tabulky se často používají v pojišťovnictví k odhadu očekávané délky života a ke stanovení pojistného. Zaměříme se na konkrétní typ tabulky života hojně používaný v biostatistické analýze, který se nazývá kohortní tabulka života nebo tabulka následného života. Tabulka následné životnosti shrnuje zkušenosti účastníků během předem definovaného období sledování v kohortové studii nebo v klinické studii až do doby, kdy nastane událost, která je předmětem zájmu, nebo do konce studie, podle toho, co nastane dříve.

Pro sestavení tabulky životnosti nejprve uspořádáme doby sledování do rovnoměrně rozložených intervalů. Ve výše uvedené tabulce máme maximální dobu sledování 24 let a uvažujeme pětileté intervaly (0-4, 5-9, 10-14, 15-19 a 20-24 let). Sečteme počet účastníků, kteří žijí na začátku každého intervalu, počet zemřelých a počet cenzurovaných v každém intervalu.

Interval v letech	Počet žijících na začátku intervalu	Počet zemřelých během intervalu	Počet cenzurovaných
0-.4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

V naší analýze tabulky životnosti používáme následující zápis. Nejprve definujeme notaci a poté ji použijeme ke konstrukci tabulky života.

• Nt = počet účastníků, kteří jsou bez události a jsou považováni za rizikové během intervalu t (např, v tomto příkladu počet žijících, protože výsledkem našeho zájmu je smrt)
• Dt = počet účastníků, kteří zemřou (nebo utrpí událost, která nás zajímá) během intervalu t
• Ct = počet účastníků, kteří jsou cenzurováni během intervalu t Nt* = průměrný počet účastníků v riziku během intervalu t
• Nt* = průměrný počet účastníků v riziku během intervalu t [Při konstrukci pojistněmatematických tabulek života se často vychází z následujících předpokladů: Předpokládá se, že k událostem, které jsou předmětem zájmu (např. úmrtí), dochází na konci intervalu a že cenzurované události se vyskytují rovnoměrně (nebo rovnoměrně) v průběhu celého intervalu. Proto se často provádí úprava Nt, která odráží průměrný počet ohrožených účastníků během intervalu, Nt*, který se vypočítá takto: Nt* =Nt-Ct/2 (tj, odečteme polovinu cenzorovaných událostí).
• qt = podíl zemřelých (nebo postižených událostí) během intervalu t, qt = Dt/Nt*
• pt = podíl přeživších (zůstávajících bez událostí) v intervalu t, pt = 1-qt
• St, podíl přeživších (nebo zůstávajících bez událostí) za intervalem t; někdy se nazývá kumulativní pravděpodobnost přežití a počítá se takto: Nejprve se podíl účastníků, kteří přežijí po uplynutí času 0 (počáteční čas), definuje jako S0 = 1 (všichni účastníci žijí nebo jsou bez události v čase nula nebo na začátku studie). Podíl účastníků, kteří přežijí každý následující interval, se vypočítá pomocí principů podmíněné pravděpodobnosti uvedených v modulu o pravděpodobnosti. Konkrétně pravděpodobnost, že účastník přežije interval 1, je S1 = p1. Pravděpodobnost, že účastník přežije přes interval 2, znamená, že musel přežít přes interval 1 a přes interval 2: S2 = P(přežije přes interval 2) = P(přežije přes interval 2)*P(přežije přes interval 1), neboli S2 = p2*S1. Obecně platí, že St+1 = pt+1*St.

Formát tabulky následného života je uveden níže.

Pro první interval, 0-4 roky: V čase 0, na začátku prvního intervalu (0-4 roky), žije nebo je ohroženo 20 účastníků. Dva účastníci v tomto intervalu zemřou a 1 je cenzurován. Použijeme korekci na počet účastníků cenzurovaných během tohoto intervalu a získáme Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Výpočty zbývajících sloupců jsou uvedeny v tabulce. Pravděpodobnost, že účastník přežije po 4 letech nebo po uplynutí prvního intervalu (při použití horní hranice intervalu pro určení času), je S4 = p4 = 0,897.

Pro druhý interval, 5-9 let: Počet ohrožených je počet ohrožených v předchozím intervalu (0-4 roky) snížený o ty, kteří zemřeli a jsou cenzurováni (tj. Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). Pravděpodobnost, že účastník přežije po 9 letech, je S9 = p9*S4 = 0,937*0,897 = 0,840.

Interval v letech	Počet ohrožených během intervalu, Nt	Průměrný počet ohrožených během intervalu, Nt*	Počet úmrtí v průběhu intervalu, Dt	Ztraceno do sledování, Ct	Podíl zemřelých Během intervalu, qt	Mezi ohroženými, podíl přeživších Interval, pt	Pravděpodobnost přežití St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

Úplná tabulka následné životnosti je uvedena níže.

Interval v letech	Počet ohrožených během intervalu, Nt	Průměrný počet ohrožených během intervalu, Nt*	Počet úmrtí v průběhu intervalu, Dt	Ztraceno do sledování, Ct	Podíl zemřelých Během intervalu, qt	Mezi ohroženými, Podíl přeživších v intervalu, pt	Pravděpodobnost přežití St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Tato tabulka využívá pojistně-matematickou metodu pro konstrukci tabulky následné životnosti, kde je doba rozdělena do rovnoměrných intervalů.

Kaplan-Meierův přístup (hranice produktu)

Problémem výše uvedeného přístupu tabulky dožití je, že pravděpodobnosti přežití se mohou měnit v závislosti na uspořádání intervalů, zejména u malých vzorků. Kaplanův-Meierův přístup, nazývaný také přístup s hranicí produktu, je populární přístup, který tento problém řeší tím, že při každém výskytu události znovu odhaduje pravděpodobnost přežití.

Vhodné použití Kaplanova-Meierova přístupu spočívá na předpokladu, že cenzura je nezávislá na pravděpodobnosti vzniku události, která je předmětem zájmu, a že pravděpodobnosti přežití jsou srovnatelné u účastníků, kteří byli do studie přijati dříve a později. Při porovnávání několika skupin je také důležité, aby tyto předpoklady byly splněny v každé srovnávací skupině a aby například cenzorování nebylo pravděpodobnější v jedné skupině než v jiné.

Následující tabulka používá Kaplan-Meierův přístup k prezentaci stejných údajů, které byly výše prezentovány pomocí přístupu založeného na tabulkách života. Všimněte si, že tabulku začínáme s časem = 0 a pravděpodobností přežití = 1. V čase 0 (výchozí hodnota nebo začátek studie) jsou všichni účastníci ohroženi a pravděpodobnost přežití je 1 (nebo 100 %). U Kaplan-Meierova přístupu se pravděpodobnost přežití vypočítá pomocí St+1 = St*((Nt+1-Dt+1)/Nt+1). Všimněte si, že výpočty pomocí Kaplanovy-Meierovy metody jsou podobné jako výpočty pomocí metody pojistně matematických tabulek života. Hlavním rozdílem jsou časové intervaly, tj. u přístupu založeného na pojistně-matematických tabulkách životnosti uvažujeme rovnoměrně rozložené intervaly, zatímco u Kaplan-Meierova přístupu používáme časy pozorovaných událostí a časy cenzorování. Výpočty pravděpodobností přežití jsou podrobně uvedeny v několika prvních řádcích tabulky.

Tabulka dožití při použití Kaplan-Meierova přístupu

Čas, Roky	Počet ohrožených Nt	Počet úmrtí Dt	Počet cenzurovaných Ct	Pravděpodobnost přežití St+1 = St*((Nt+1-.Dt+1)/Nt+1)
0	20			1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3		3	0,507

Při velkých souborech dat jsou tyto výpočty únavné. Tyto analýzy však lze vytvářet pomocí programů pro statistické výpočty, jako je SAS. K výpočtu pravděpodobností přežití lze také použít program Excel, jakmile jsou data uspořádána podle časů a jsou shrnuty počty událostí a cenzorovaných časů.

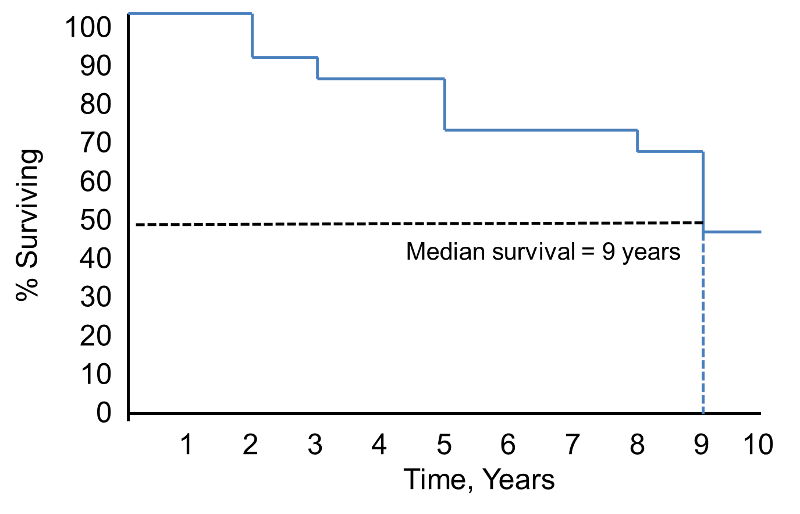
Z tabulky životnosti můžeme vytvořit Kaplanovu-Meierovu křivku přežití.

Kaplanova-Meierova křivka přežití pro výše uvedená data

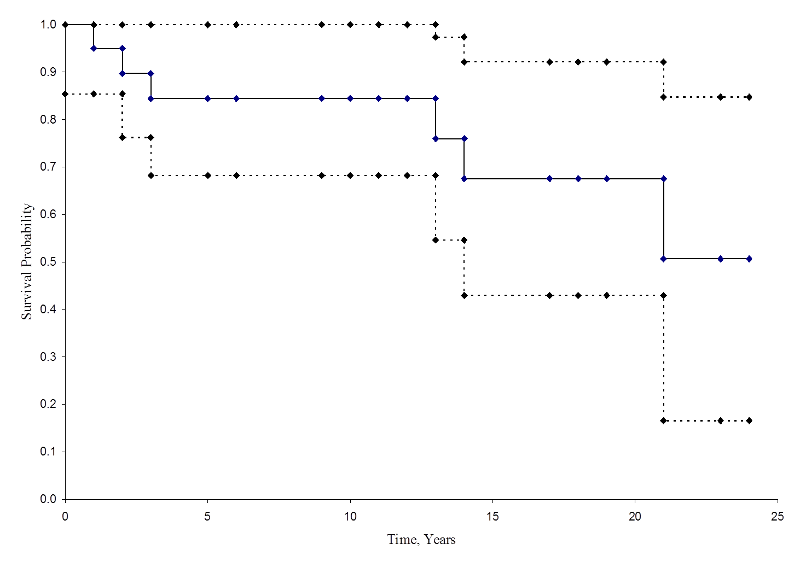
Ve výše uvedené křivce přežití představují symboly každý čas události, buď úmrtí, nebo cenzurovaný čas. Z křivky přežití můžeme také odhadnout pravděpodobnost, že účastník přežije déle než 10 let, a to tak, že na ose X najdeme 10 let a odečteme je nahoru a na osu Y. Podíl účastníků, kteří přežijí 10 let, je 84 % a podíl účastníků, kteří přežijí 20 let, je 68 %. Medián přežití se odhadne tak, že se na ose Y umístí hodnota 0,5 a odečte se od osy X směrem nahoru a dolů. Medián přežití je přibližně 23 let.

Standardní chyby a odhady intervalů spolehlivosti pravděpodobností přežití

Tyto odhady pravděpodobností přežití v konkrétních časech a mediánu doby přežití jsou bodové odhady a jako takové by měly být interpretovány. Existují vzorce pro tvorbu standardních chyb a odhadů intervalů spolehlivosti pravděpodobností přežití, které lze vytvořit pomocí mnoha statistických výpočetních balíků. Oblíbený vzorec pro odhad směrodatné chyby odhadů přežití se nazývá Greenwoodův5 vzorec a je následující:

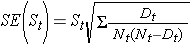
Veličina 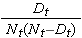se sečte pro počty ohrožených (Nt) a počty úmrtí (Dt), ke kterým došlo do doby zájmu (tj. kumulativně, ve všech dobách před dobou zájmu, viz příklad v tabulce níže). Pro odhady přežití pro údaje v tabulce níže jsou vypočteny standardní chyby. Všimněte si, že v posledním sloupci je uvedena veličina 1,96*SE(St), která představuje chybové rozpětí a používá se pro výpočet 95% intervalu spolehlivosti odhadů (tj. St ± 1,96 x SE(St)).

Standardní chyby odhadů přežití

Čas, Roky	Počet ohrožených Nt	Počet zemřelých Dt	Přežití Pravděpodobnost St				1.96*SE (St)
0	20		1		.
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0,000	0,118	0,174	0,341

Na následujícím obrázku jsou shrnuty odhady a intervaly spolehlivosti. Kaplanova-Meierova křivka přežití je znázorněna plnou čarou a 95% meze spolehlivosti jsou znázorněny tečkovanými čarami.

Kaplanova-Meierova křivka přežití s intervaly spolehlivosti

Křivky kumulativní incidence

Někteří vyšetřovatelé dávají přednost vytváření křivek kumulativní incidence na rozdíl od křivek přežití, které ukazují kumulativní pravděpodobnosti výskytu události, která je předmětem zájmu. Kumulativní incidence nebo kumulativní pravděpodobnost selhání se počítá jako 1-St a lze ji snadno vypočítat z tabulky životnosti pomocí Kaplanovy-Meierovy metody. Kumulativní pravděpodobnosti selhání pro výše uvedený příklad jsou uvedeny v následující tabulce.

Tabulka životnosti s kumulativními pravděpodobnostmi selhání

Čas, Roky	Počet ohrožených Nt	Počet úmrtí Dt	Počet Cenzurovaných Ct	Pravděpodobnost přežití St	Pravděpodobnost selhání 1-.St
0	20			1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0,493

Následující obrázek ukazuje kumulativní výskyt úmrtí u účastníků zařazených do výše popsané studie.

Křivka kumulativní incidence

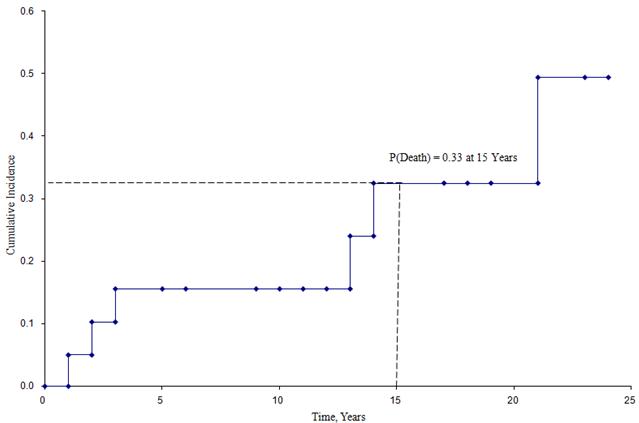
Z tohoto obrázku můžeme odhadnout pravděpodobnost, že účastník zemře do určitého časového bodu. Například pravděpodobnost úmrtí v 15 letech je přibližně 33 % (viz čárkované čáry).

zpět na začátek | předchozí stránka | další stránka

.