Podle Evana Ma

(lektor matematiky a fyziky ve vzdělávacím centru The Edge)

Zdá se, že logaritmická funkce mate mnoho studentů studujících program IB Math SL. Abychom ji správně pochopili, definujme

kde , přísně kladné reálné číslo, se nazývá základ a je mocnina. Všichni například známe nazpaměť:

a tak dále. Logaritmická funkce to dělá obráceně – při zadání čísla jako argumentu získá mocninu s výhradou zadaného základu, a proto je definována takto.

Jestliže

tedy

Je tedy jasné, že

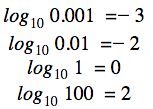
a tak dále. Podívejme se na další příklady zahrnující jiné základy:

Napišme si na procvičení následující otázky: (a) , (b) , (c) , (d) . Odpovědi naleznete na konci tohoto blogu.

Z definice logaritmu také vyplývá, že pokud zvýšíme základ o základ-logaritmu reálného čísla , dostaneme zpět číslo , viz

Můžete si to zkusit ověřit pomocí kalkulačky pro různé platné základy. Tato identita je důležitá, když se snažíme řešit logaritmické rovnice, jejichž příklady budou uvedeny alter.

Nyní se podíváme na pravidla logaritmu. Podobně jako při definici logaritmu využijeme k odvození pravidel zákony indexů:

1. Logaritmus součinu je součet logaritmů

Důkaz: Řekněme a , tedy

2. Základní logaritmus součinu Mr je krát

Důkaz: Řekněme , tedy

3. Logaritmus kvocientu je rozdíl logaritmů

Důkaz: Řekněme a , tedy

4. Poslední pravidlo se nazývá vzorec pro změnu základu. Jako pomůcku pro odvození vzorce použijeme příklad. Řekněme, že chceme vědět, o jakou mocninu musíme zvýšit číslo 2, abychom dostali číslo 50. Protože 50 není celočíselnou mocninou 2, není odpověď příliš zřejmá. Proto píšeme

a tedy. Abychom zjistili , řekněme, že na obě strany rovnice aplikujeme logaritmus o základu 10, protože naše kalkulačka nemusí mít klávesu pro logaritmus o základu 2:

Po opravě na 4 platné číslice je hodnota přibližně 5,644. V případě, že bude mít logaritmus o základu 2, bude hodnota přibližně 5,644. Ve skutečnosti si můžete odpověď ověřit tak, že zvýšíte číslo 2 na mocninu čísla 5,644 a zjistíte, že odpověď je přibližně 50.

Chceme-li problém zobecnit, řekněme, že musíme najít takovou, že a základnu- logaritmu nemáme k dispozici, můžeme tedy místo toho použít logaritmus báze- podle rovnice

a tedy

Například uvažujme následující. Předpokládejme, že je uložena částka 10 000 USD s úrokem 2,5 % ročně, složeným ročně. Jak dlouho musí být peníze na účtu, aby vzrostly na 50 000 USD?

Chceme-li odpovědět na otázku, snažíme se v podstatě najít n takové, že

Protože moje jednoduchá vědecká kalkulačka neumožňuje zadat základ 1.025 pro logaritmický klíč, budu se muset spolehnout na vzorec pro změnu základu a použít základ 10, a tedy

Protože se úrok skládá ročně, bude trvat 66 let, než vzroste alespoň pětkrát.

Pokud jsme prozkoumali pravidla logaritmů, zavedeme přirozenou logaritmickou funkci neboli . Je to základ-, kde je význačné iracionální číslo ≈2,71828 a jehož význam ve vědách a matematice nelze dostatečně zdůraznit. Základnílogaritmus je tedy definován takto:

Jestliže

tedy

Dále se podíváme na dva příklady, kde se dělají časté chyby při řešení logaritmických rovnic. Zjistěte, zda dokážete chybu identifikovat.

Kde je chyba? Podívejte se blíže. Ve druhém kroku samozřejmě nelze “rozdělit” logaritmus přes znaménko sčítání. Nezapomeňte, že “rozdělit” logaritmus na součet lze pouze v případě, že je logaritmus aplikován na součin, nikoliv na součet. Správné kroky jsou tedy následující:

Nyní se podívejme na následující příklad a uvidíme, zda dokážete identifikovat chybu:

Kde je chyba? Ano, je ve druhém kroku – kvocient logaritmů samozřejmě není logaritmem kvocientu. Pro zjednodušení prvního kroku můžeme spíše použít vzorec pro změnu základu, a to takto:

Nakonec si ukážeme, jak využít pravidla logaritmu k řešení následujícího:

Můžete si všimnout, že neznámá vystupuje jako základ a proměnná v argumentu logaritmu. Jak můžeme vyřešit? Metoda stále závisí na důsledném použití pravidel logaritmování. Nejprve obě strany zvýšíme jako mocniny základu , a tedy

Možná si z definice logaritmu vzpomenete, že levá strana se právě stane argumentem logaritmu, a proto

Přeuspořádáním výše uvedené rovnice musíme vyřešit

Pozorujeme-li, že se to podobá kvadrátu v , vyřešíme takto:

Kde je nyní záporný kořen? Protože je zároveň základem logaritmu, záporný kořen tedy jako řešení odmítáme. Konečnou odpovědí je tedy .

Přehledem výše uvedených příkladů se můžete přesvědčit, že vyřešit zdánlivě obtížnou logaritmickou rovnici není vůbec těžké – stačí důsledně aplikovat pravidla logaritmování a správné řešení lze získat.

Odpovědi na otázky: (a) 2 b) 3 c) -3 d) -2

.