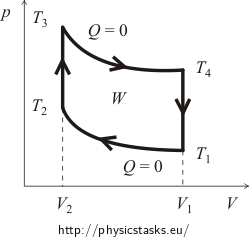
Na začátku je obvykle nutné získat představu o pV diagramu cyklu. Za tímto účelem budeme sledovat křivky izochorického a adiabatického děje. Přibližný graf Ottova cyklu je znázorněn na následujícím obrázku.

Účinnost η cyklu je definována jako

\

kde W je práce vykonaná plynem během jednoho cyklu minus práce vykonaná vnějšími silami (v diagramu je znázorněna plochou plochy vymezené přímkami cyklu!) a Qsup je teplo dodané soustavě během cyklu.

Práci W lze vypočítat pomocí vztahu mezi tlakem a objemem během adiabatické expanze a komprese (práce vykonaná během izochorického procesu je samozřejmě nulová). V této úloze však bude lepší využít toho, že celková změna vnitřní energie za cyklus musí být rovna nule (dostáváme se zpět do stejného stavu jako na začátku, proto teplota a tedy i vnitřní energie zůstávají stejné!) Podle prvního termodynamického zákona lze práci vykonanou plynem vyjádřit jako rozdíl mezi dodaným teplem Qsup a uvolněným teplem Qrel. Vzorec pro účinnost cyklu má tedy tvar

\

Nejprve vypočítáme dodané teplo Qsup. Je zřejmé, že při adiabatickém procesu nedochází k výměně tepla a při izochorickém ochlazování se teplo uvolňuje. To znamená, že teplo bude dodáno pouze během izochorického ohřevu z teploty T2 na teplotu T3. Množství tohoto tepla lze vyjádřit veličinami látkové množství n plynu a jeho molární tepelná kapacita CV takto:

\

Velmi podobně vyjádříme množství uvolněného tepla Qrel. Již víme, že teplo se uvolňuje pouze při izochorickém ochlazování z teploty T4 zpět na počáteční teplotu T1. Platí, že:

\

Nyní dosadíme tyto vzorce do vzorce účinnosti cyklu a okamžitě dostaneme:

\ \

Nyní budeme muset vyjádřit teplotní rozdíly pomocí daného kompresního poměru

\

a Poissonova poměru κ.

K tomu použijeme rovnici pro ideální plyn procházející adiabatickým procesem (Poissonův zákon) pVκ = C = konst., kde C je konstanta. Nyní vyhodnotíme tlak ze stavové rovnice ideálního plynu

\

, který dosadíme do Poissonova zákona. Nyní převedeme konstanty (C a K) na jednu stranu

\

Tento Poissonův zákon nyní použijeme pro oba adiabatické procesy. Pro adiabatickou expanzi dostaneme vztah

\

A pro adiabatickou kompresi dostaneme

\

Nyní odečteme druhou rovnici od první a vynásobíme V1κ – 1 na jedné straně a V2κ – 1 na straně druhé. Dostaneme:

\ \

Vidíme, že se nám skutečně podařilo vyjádřit teplotní rozdíly pomocí daných hodnot. Nyní dosadíme tento vztah do vzorce pro účinnost a dostaneme konečnou rovnici:

\ \