|
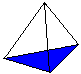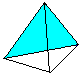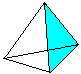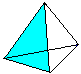
Co je to tetraedr?
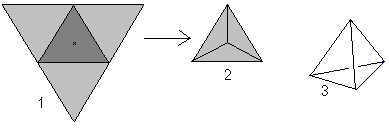
Podíváte-li se na slovo tetraedr (tetraedr znamená “se čtyřmi rovinami”), můžete každý jehlan s trojúhelníkem jako základnou nazvat tetraedrem.
Takže tetraedr je na této stránce rovný, pravidelný trojboký jehlan.
DílkyTetraedru
Výška a plocha příčného trojúhelníku
Čtyři rovnostranné trojúhelníky tvoří tetraedr.
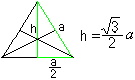 … … |
Vyznačí se trojúhelník: Tři výšky se protínají v jednom bodě jako v každém trojúhelníku. To je střed trojúhelníku. Výšku lze vypočítat podle strany a jako h=sqr(3)/2*a s použitím Pythagorovy věty. |
Výšky jsou také středy a protínají se v poměru2:1. Výšky jsou také středy. Toho využijeme v následujících výpočtech.
Plocha trojúhelníku je A=sqr(3)/4*a².
Výška prostoru
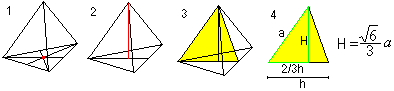
Střed, kružnice a vepsaná koule
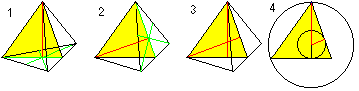
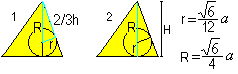 … … |
PomocíPythagorovy věty (1) a H=R+r (2) získáte dva vzorce pro r a R: Tady je r=sqr(6)/12*a , R=sqr(6)/4*a. |
Úhlová plocha
…. 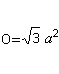 ….. ….. |
Plocha podstavy a bočních stěn tvoří plochuO. Existuje O=4*A (trojúhelník) = sqr(3)a². |
Objem

Tetraedr Čísla vrchol
… …. …. |
Přilepíte-li 20 kuliček do dvou skupin po čtyřech a dvou po šesti, dostanete známý hlavolam: Musíte vytvořit pyramidu ze čtyřdílů. |
Podobných hlavolamů je mnoho.
Tetraedr v krychli nahoře
Šest úhlopříček stěn tvoří v krychli tetraedr.
Pokud znáte trojrozměrné zobrazení, můžete se trojrozměrně podívat na následující dvě dvojice krychlí.
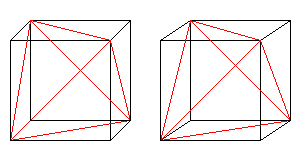
Pokud nakreslíte druhý čtyřstěn a průsečnice, získáte průnik dvou čtyřstěnů.
Obrázek se skládá z čelních úhlopříček a spojnic středů bočních čtverců původní krychle. Posledníz nich tvoří osmistěn.
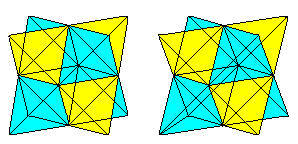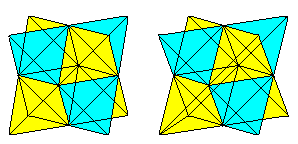
Kruhy čtyřstěnů nahoře
Můžete si vyrobit papírové čtyřstěny a nalepit jich sudý počet do kruhu. Kroužek se může neustále stáčet dovnitř nebo ven středem. Je to pěkná hračka. – Těmto kroužkům se také říká kaleidocykly, více najdete na mé webové stránce Kaleidocykly.
Tetrahedraon Internettop
Němčina
Christof Weber
Washat dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)
Albert Kluge
Einrotierender Tetraeder als Java-Applet
FAZ
Tetraederpackung:Eins geht noch
Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)
Gerd Müller
PlatonischeKörper in Stereodarstellung
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder
LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder
ruhr-guide
TetraederBottrop
Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl
English
Eric W. Weisstein (World of Mathematics)
Tetrahedron
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetrahedron
Joyce Frost a Peg Cagle (mathforum)
Úžasný, prostor vyplňující, nepravidelný tetrahedron
Wikipedia
Tetrahedron,Tetrapod(struktura), Tetrahedralnumber