6.3 Sítě víry
Pojmem podmíněné nezávislosti lze stručně reprezentovat mnoho domén. Jde o to, že při dané náhodné proměnné X může existovat malá množina proměnných, kterépřímo ovlivňují hodnotu proměnné v tom smyslu, že X jepodmíněně nezávislá na ostatních proměnných daných hodnotami přímo ovlivňujících proměnných. Množina lokálně ovlivňujících proměnných se nazývá Markovova deka. Tato lokálnost je to, co se využívá v síti víry. Síť víry je směrovaný model podmíněné závislosti mezi množinou náhodných proměnných. Přesné vyjádření podmíněné nezávislosti v síti víry bere v úvahu směrovost.
Chcete-li definovat síť víry, začněte s množinou náhodných proměnných, které reprezentují všechny vlastnosti modelu. Předpokládejme, že tyto proměnné jsou {X1,…,Xn}.
Předpokládejme, že tyto proměnné jsou {X1,…,Xn}.
Pravidlo řetězce (věta 6.3) ukazuje, jak rozložit konjunkci na podmíněné pravděpodobnosti:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Nebo z hlediska náhodných veličin a rozdělení pravděpodobnosti,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Definice rodičů náhodné proměnné Xi, psánoparents(Xi), je aminimální množina předchůdců Xi v celkovém uspořádání taková, že ostatní předchůdci Xi jsou podmíněně nezávislí na Xi vzhledem kparents(Xi). To znamená, že parents(Xi) ⊆{X1,…,Xi-1} tak, že
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
Pokud existuje více než jedna minimální množina, lze za rodiče zvolit libovolnou minimální množinu. Více než jedna minimální množina může existovat pouze tehdy, když někteří z předchůdců jsou deterministickými funkcemi jiných.
Můžeme dát dohromady řetězové pravidlo a definici rodičů,čímž získáme
P(X1, X2,—, Xn) = ∏i=1n P(Xi|rodiče(Xi)).
Pravděpodobnost nad všemi proměnnými, P(X1, X2,—,Xn), se nazývá společné rozdělení pravděpodobnosti. Síť přesvědčení definujefaktorizaci společného rozdělení pravděpodobnosti, kde podmíněné pravděpodobnosti tvoří faktory, které se násobí.
Síť přesvědčení, nazývaná také Bayesova síť, je acyklickýorientovaný graf (DAG), jehož uzly jsou náhodné veličiny. Z každého prvkuparents(Xi) vede oblouk do Xi.Se sítí víry je spojena množina podmíněných rozdělení pravděpodobnosti – podmíněná pravděpodobnost každé proměnné vzhledem k jejím rodičům (která zahrnuje předběžné pravděpodobnosti těch proměnných, které nemají rodiče).
Síť přesvědčení se tedy skládá z
- DAG, kde je každý uzel označen náhodnou proměnnou;
- oblasti pro každou náhodnou proměnnou; a
- souboru podmíněných rozdělení pravděpodobnosti udávajících P(X|rodiče(X)) pro každou proměnnou X.
Síť přesvědčení je konstrukčně acyklická. Způsob, jakým se řetězově řízenákonjunkce skládá, udává její uspořádání. Proměnná může mít jako rodiče pouze předchůdce.
Předpokládejme, že použijeme následující proměnné, z nichž všechny jsou logické, v následujícím pořadí:
- Tampering je pravdivý, pokud došlo k manipulaci s alarmem.
- Požár je pravda, když dojde k požáru.
- Alarm je pravda, když zazní alarm.
- Kouř je pravda, když je kouř.
- Odchod je pravda, když budovu opouští mnoho lidí najednou.
- Hlášení je pravda, když někdo podá hlášení o odchodu lidí. Hlášení je nepravdivé, pokud neexistuje žádné hlášení o odchodu.
Proměnná Hlášení označuje hlášení senzoru, že lidé odcházejí. Tato informace je nespolehlivá, protože osoba, která takové hlášení vydala, si mohla dělat legraci, nebo nikdo, kdo by takové hlášení mohl podat, nemusel dávat pozor. Tato proměnná je zavedena, aby umožnila podmínit nespolehlivé údaje ze senzorů. Agent ví, co senzor hlásí,ale má pouze nespolehlivé důkazy o osobách opouštějících budovu.Jako součást domény předpokládejte následující podmíněné nezávislosti:
- Požár je podmíněně nezávislý na manipulaci (za předpokladu, že nemá žádné jiné informace).
- Poplach závisí na požáru i manipulaci. To znamená, že nepředpokládáme žádnou nezávislost na tom, jak Alarm závisí na svých předchůdcích vzhledem k tomuto uspořádání proměnných.
- Kouř závisí pouze na Požáru a je podmíněně nezávislý na Tamperingu a Alarmu vzhledem k tomu, zda existuje Požár.
- Odchod závisí pouze na Alarmu a ne přímo na Požáru neboTamperingu nebo Kouři. To znamená, že Odcházení je podmíněně nezávislé na ostatních proměnných vzhledem k Poplachu.
- Hlášení závisí přímo pouze na Odcházení.
Tyto závislosti vyjadřuje síť přesvědčení na obrázku 6.1.
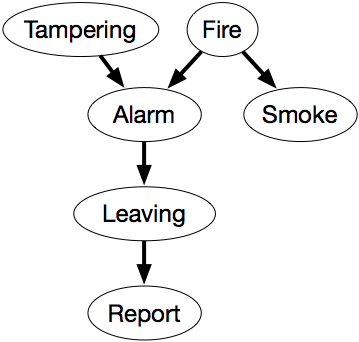
Tato síť představuje faktorizaci
P(Tampering,Fire,Alarm,Smoke,Leaving,Hlášení) = P(Tampering) ×P(Fire) ×P(Alarm|Tampering,Fire) ×P(Smoke|Fire) ×P(Leaving|Alarm) ×P(Report|Leaving).
Také musíme definovat doménu každé proměnné. Předpokládejme, že proměnné jsou logické, to znamená, že mají doménu {pravda,nepravda}. Pro vyjádření pravdivé hodnoty použijeme variantu proměnné s malými písmeny a pro nepravdivou hodnotu použijeme negaci. Tak například Tampering=true se zapíše jako tampering aTampering=false se zapíše jako ¬tampering.
Následující příklady předpokládají následující podmíněné pravděpodobnosti:
P(fire) = 0,01
P(alarm | fire ∧tampering) = 0.5
P(alarm | požár ∧¬tamperování) = 0,99
P(alarm | ¬požár ∧tamperování) = 0,85
P(alarm | ¬požár ∧¬tamperování) = 0,0001
P(kouř | požár ) = 0.9
P(kouř | ¬požár ) = 0,01
P(odchod | alarm) = 0,88
P(odchod | ¬alarm ) = 0,001
P(hlášení | odchod ) = 0,75
P(hlášení | ¬odchod ) = 0.01
- Pro každý vodič wi existuje náhodná proměnná Wi, sdoménou {živý,mrtvý}, která označuje, zda je ve vodiči wi energie. Wi=live znamená, že wirewi má napájení. Wi=dead znamená, že ve vodiči wi není žádný proud.
- Outside_power s doménou {live,dead} označuje, zda do budovy přichází proud.
- Pro každý spínač si označuje proměnná Si_pos polohu si. Má doménu {nahoru,dolů}.
- Pro každý spínač si označuje proměnná Si_st stav spínače si. Má doménu {ok,upside_down,short,intermittent,broken}. Si_st=ok znamená, že spínač si pracuje normálně. Si_st=upside_down znamená, že spínač je nainstalován vzhůru nohama. Si_st=zkrat znamená, že spínač si je zkrácený a funguje jako drát. Si_st=porušený znamená, že spínač si jeporušený a neumožňuje průtok elektřiny.
- Pro každý vypínač obvoduercbi má proměnná Cbi_st doménu {zapnuto,vypnuto}. Cbi_st=zapnuto znamená, že přes cbi může proud proudit a Cbi_st=vypnuto znamená, že přes cbi nemůže proud proudit.
- Pro každé světlo li označuje proměnná Li_st s doménou {ok,přerušovaný,rozbitý} stav světla. Li_st=ok znamená, že světlo li bude svítit, pokud je napájeno, Li_st=intermittent znamená, že světlo li přerušovaně svítí, pokud je napájeno, a Li_st=broken znamená, že světlo li nefunguje.
Zvolíme uspořádání, kde příčiny proměnné jsou v uspořádání před proměnnou. Například proměnná pro to, zda světlo svítí, je až za proměnnými pro to, zda světlo funguje a zda do světla přichází proud.
Zda světlo l1 svítí, závisí pouze na tom, zda je ve vodiči w0 proud a zda světlo l1 správně funguje. Ostatní proměnné, jako je poloha spínače s1, zda svítí světlo l2 nebo kdo je královnou Kanady, jsou irelevantní. Rodiči proměnné L1_lit jsou tedy proměnné W0 a L1_st.
Uvažujme proměnnou W0, která představuje, zda je ve vodiči w0 proud. Pokud bychom věděli, zda je ve vodičích w1 aw2 proud, a znali bychom polohu spínače s2 a věděli bychom, zda spínač funguje správně, hodnota ostatních proměnných (kroměL1_lit) by neměla vliv na naše přesvědčení, zda je ve vodiči w0 proud. Rodiči W0 by tedy měly být S2_Pos, S2_st,W1 a W2.
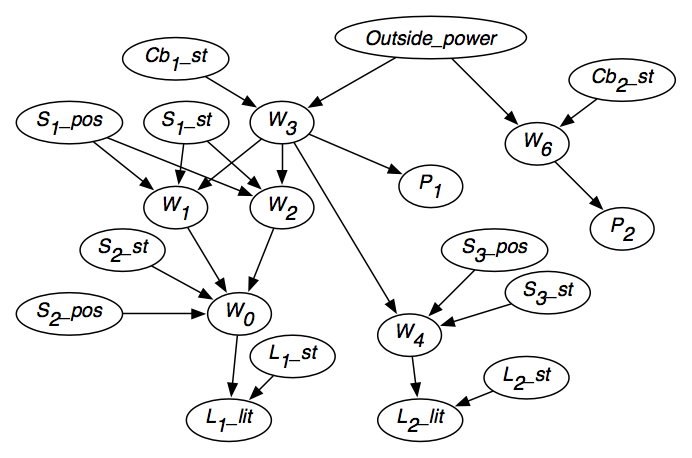
Obrázek 6.2 ukazuje výslednou síť přesvědčení po zohlednění nezávislosti jednotlivých proměnných. síť přesvědčení obsahuje také domény proměnných, jak je uvedeno na obrázku, a podmíněné pravděpodobnosti každé proměnné vzhledem k jejím rodičům.
Pro proměnnou W1 je třeba zadat následující podmíněné pravděpodobnosti:
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
…. P(W1=živý|S1_pos=dolů ∧S1_st=zlomený ∧W3=mrtvý).
Existují dvě hodnoty pro S1_pos, pět hodnot pro S1_ok a dvě hodnoty pro W3, takže existuje 2×5 ×2 = 20 různýchpřípadů, kdy musí být zadána hodnota pro W1=živý. Pokud jde o teorii pravděpodobnosti, pravděpodobnost pro W1=live pro těchto 20 případů může být přiřazena libovolně. Znalost domény samozřejmě omezuje, jaké hodnoty mají smysl. Hodnoty pro W1=mrtvý lze vypočítat z hodnot pro W1=živý pro každý z těchto případů.
Protože proměnná S1_st nemá žádné rodiče, vyžaduje apriorní rozdělení, které lze zadat jako pravděpodobnosti pro všechny hodnoty kromě jedné; zbývající hodnota může být odvozena z omezení, že všechny pravděpodobnosti jsou rovny 1. Pro určení rozdělení S1_st je tedy třeba zadat čtyři z následujících pěti pravděpodobností:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Síť přesvědčení je grafickým znázorněním podmíněné nezávislosti. nezávislost nám umožňuje zobrazit přímé účinky v rámci grafua předepisuje, které pravděpodobnosti musí být uvedeny. Ze sítě lze odvodit libovolnépostupné pravděpodobnosti.
Předpoklad nezávislosti obsažený v síti přesvědčení je následující: Každá náhodná proměnná je podmíněně nezávislá na svých nepostupujících proměnných vzhledem ke svým rodičům. To znamená, že pokud je X náhodná proměnná s rodiči Y1,…, Yn, všechny náhodné proměnné, které nejsou potomkyX, jsou podmíněně nezávislé na X vzhledem k Y1 ,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
pokud R nezahrnuje potomka X. Pro tuto definici zahrnujeme X jako potomka sebe sama. Pravá strana této rovnice je tvar pravděpodobností, kteréjsou specifikovány jako součást sítě přesvědčení.R může zahrnovat předky X a další uzly, pokud nejsou potomky X. Předpoklad nezávislosti říká, že veškerý vliv proměnných, které nejsou potomky, je zachycen znalostí hodnoty rodičů X.
Často označujeme jako síť přesvědčení pouze označenou DAG. Při tom je důležité mít na paměti, že součástí sítě je také doména každé proměnné a soubor podmíněných rozdělení pravděpodobnosti.
Počet pravděpodobností, které je třeba určit pro každou proměnnou, je exponenciální v počtu rodičů proměnné.
Předpoklad nezávislosti je užitečný do té míry, že počet proměnných, které přímo ovlivňují jinou proměnnou, je malý. Měli byste uspořádat proměnné tak, aby uzly měly co nejmenší počet rodičů.
Sítě víry a kauzalita
Sítě víry se často nazývají kauzálními sítěmi a tvrdí se o nich, že jsou dobrou reprezentací kauzality.Připomeňme, že kauzální model předpovídá výsledek zásahů.Předpokládejme, že máte k dispozici kauzální model domény, kde je doména specifikována v podobě množiny náhodných proměnných. Pokud pro každou dvojici náhodných proměnných X1a X2 existuje přímá příčinná souvislost z X1 do X2(tj. zásah, který změní X1 v určitém kontextu jiných proměnných, ovlivní X2 a nelze to modelovat pomocí nějaké intervenující proměnné), přidejte oblouk zX1 do X2. Dalo by se očekávat, že kauzální model bude splňovat předpoklad nezávislosti sítě víry. Platily by tedy všechnyzávěry sítě přesvědčení.
Očekávali byste také, že takový graf bude acyklický; nechcete, aby něco nakonec způsobilo samo sebe. Tento předpoklad je rozumný, pokud uvážíte, že náhodné veličiny představují spíše konkrétní události než typy událostí. Uvažujme například kauzální řetězec, že “býtve stresu” způsobuje, že “pracujete neefektivně”, což zase způsobuje, že “jste ve stresu”. Abychom přerušili zdánlivý cyklus, můžeme “být ve stresu” v různých fázích reprezentovat jako různé náhodné veličiny, které se vztahují k různým časům. Býtstresován v minulosti způsobuje, že v daném okamžiku nepracujete dobře, což způsobuje, že jste stresován v budoucnosti. Proměnné by mělysplňovat zásadu jasnosti a mít dobře definovaný význam. Proměnnéby neměly být chápány jako typy událostí.
Síť přesvědčení sama o sobě nemá co říci o kauzalitě a může reprezentovat nekauzální nezávislost, ale zdá se, že je vhodná zejména tehdy, když v doméně existuje kauzalita. Přidáním oblouků, které představují lokální kauzalitu, vzniká malá síť přesvědčení. Síť přesvědčení naobrázku 6.2 ukazuje, jak to lze provést pro jednoduchou doménu.
Akauzální síť modeluje zásahy. Pokud by někdo uměle donutil proměnnou, aby měla určitou hodnotu, ovlivnilo by to její potomky – ale žádné jiné uzly. Nakonec se můžete podívat, jak kauzalita v sítích přesvědčení souvisí s kauzálními a důkazními úvahami, o nichž jsme hovořili v oddíle 5.7. Na kauzální síť přesvědčení lze pohlížet jako na axiomatizaci v kauzálním směru. Zdůvodňování v sítích přesvědčeníodpovídá abdukci na příčiny a následnémupředvídání z nich. Mezi logickým abdukčním pohledem, o němž pojednává oddíl 5.7, a sítěmi přesvědčení existuje přímé propojení: Sítě přesvědčení lze modelovat jako logické programy s pravděpodobnostmi nad možnými hypotézami. To je popsáno v oddíle 14.3.
Všimněte si v definici nezávislosti zakódované v síti přesvědčení omezení “každá náhodná veličina je podmíněně nezávislá na svých ne-příbuzných vzhledem ke svým rodičům”. PokudR obsahuje potomka proměnné X, předpoklad nezávislosti nenípřímo použitelný.
Proměnná S1_pos nemá žádné rodiče. Nezávislost zakotvená v síti přesvědčení tedy určuje, že P(S1_pos=up|A) =P(S1_pos=up) pro libovolné A, které nezahrnuje potomkaS1_pos. Pokud A zahrnuje potomka S1_pos=up – například pokud A je S2_pos=up∧L1_lit=pravda – nelze předpoklad nezávislosti přímo použít.
Tuto síť lze použít několika způsoby:
- Podmíněním znalosti, že spínače a jističe jsou v pořádku, a hodnotami vnějšího výkonu a polohy spínačů může tato síť simulovat, jak by mělo osvětlení fungovat.
- Při daných hodnotách vnějšího výkonu a poloze vypínačů může síť odvodit pravděpodobnost jakéhokoli výsledku – například jak pravděpodobné je, že se rozsvítí l1.
- Díky hodnotám spínačů a tomu, zda světla svítí, lze odvodit posteriorní pravděpodobnost, že každý spínač nebo jistič je v nějakém konkrétním stavu.
- Díky některým pozorováním lze síť použít ke zpětné úvaze a určit nejpravděpodobnější polohu spínačů.
- Díky některým polohám spínačů, některým výstupům a některým mezilehlým hodnotám lze síť použít k určení pravděpodobnosti jakékoli jiné proměnné v síti.
Síť víry určuje společné rozdělení pravděpodobnosti, ze kterého lze odvodit libovolné podmíněné pravděpodobnosti. Síť lze dotazovat dotazem na podmíněnou pravděpodobnost libovolné proměnné podmíněnou hodnotami libovolných jiných proměnných. To se obvykle provádí tak, že se zadají pozorování některých proměnných a dotaz na jinou proměnnou.
P(požár) = 0,01
P(hlášení ) = 0,028
P(kouř) = 0.0189
Při sledování hlášení dostaneme následující:
P(požár |hlášení)= 0,2305
P(kouř |hlášení) = 0,215
Podle očekávání se pravděpodobnost sabotáže i požáru zvyšuje o hlášení. Protože se zvyšuje pravděpodobnost požáru, zvyšuje se i pravděpodobnost kouře.
Předpokládejme místo toho, že byl pozorován kouř:
P(požár|kouř) = 0,476
P(hlášení |kouř) = 0,320
Všimněte si, že pravděpodobnost manipulace není pozorovánímkouře ovlivněna; pravděpodobnosti hlášení a požáru se však zvyšují.
Předpokládejme, že bylo pozorováno hlášení i kouř:
P(požár |hlášení ∧kouř) = 0,964
Při pozorování obou se pravděpodobnost požáru ještě zvyšuje. Vkontextu hlášení však přítomnost kouře činí manipulaci méně pravděpodobnou. Je to proto, že hlášení je vysvětleno požárem, který je nyní pravděpodobnější.
Předpokládejme místo toho, že bylo pozorováno hlášení, ale ne kouř:
P(požár|hlášení ∧¬kouř) = 0,0294
V kontextu hlášení se požár stává mnohem méně pravděpodobným a pro vysvětlení hlášení se zvyšuje pravděpodobnost manipulace.
Tento příklad ilustruje, jak předpoklad nezávislosti sítě přesvědčení dává společnézávěry, a také ukazuje, jak je vysvětlení pryč důsledkem předpokladu nezávislosti sítě přesvědčení.
- 6.3.1 Konstrukce sítí přesvědčení
.