Průtok StatsTestu: Predikce >> Spojitá závislá proměnná >> Více než jedna nezávislá proměnná >> Bez opakovaných měření >> Jedna závislá proměnná
Nejste si jisti, že je to správná statistická metoda? Pro výběr správné metody použijte pracovní postup Choose Your StatsTest.
- Co je vícerozměrná vícenásobná lineární regrese?
- Předpoklady pro vícerozměrnou lineární regresi
- Linearita
- Žádné odlehlé hodnoty
- Podobný rozptyl v celém rozsahu
- Normálnost reziduí
- Žádná multikolinearita
- Kdy použít vícerozměrnou lineární regresi?
- Předpověď
- Spojitá závislá proměnná
- Více než jedna nezávislá proměnná
- Příklad vícerozměrné vícenásobné lineární regrese
- Často kladené otázky
- Nápověda!”
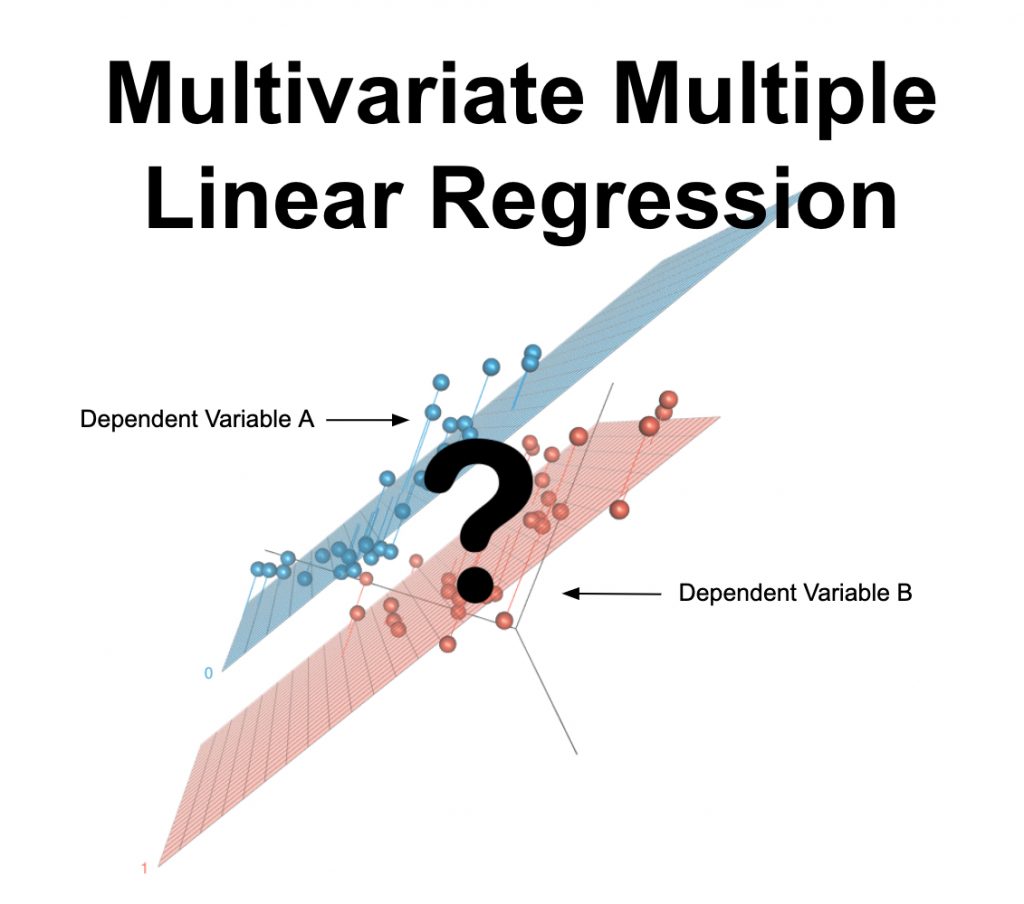
Co je vícerozměrná vícenásobná lineární regrese?
Vícerozměrná vícenásobná lineární regrese je statistický test používaný k předpovědi více výsledných proměnných pomocí jedné nebo více jiných proměnných. Používá se také k určení číselného vztahu mezi těmito soubory proměnných a ostatními. Proměnná, kterou chcete předpovídat, by měla být spojitá a vaše data by měla splňovat další předpoklady uvedené níže.
Předpoklady pro vícerozměrnou lineární regresi
Každá statistická metoda má předpoklady. Předpoklady znamenají, že vaše data musí splňovat určité vlastnosti, aby výsledky statistické metody byly přesné.
Mezi předpoklady pro vícerozměrnou vícenásobnou lineární regresi patří:
- Linearita
- Žádné odlehlé hodnoty
- Podobný rozptyl v celém rozsahu
- Normálnost reziduí
- Žádná multikolinearita
Ponoříme se do každého z nich zvlášť.
Linearita
Proměnné, které vás zajímají, spolu musí souviset lineárně. To znamená, že pokud proměnné vynesete do grafu, budete moci nakreslit přímku, která odpovídá tvaru dat.
Žádné odlehlé hodnoty
Proměnné, které vás zajímají, nesmí obsahovat odlehlé hodnoty. Lineární regrese je citlivá na odlehlé hodnoty neboli datové body, které mají neobvykle velké nebo malé hodnoty. To, zda vaše proměnné obsahují odlehlé hodnoty, poznáte tak, že je vynesete do grafu a sledujete, zda jsou některé body daleko od všech ostatních bodů.
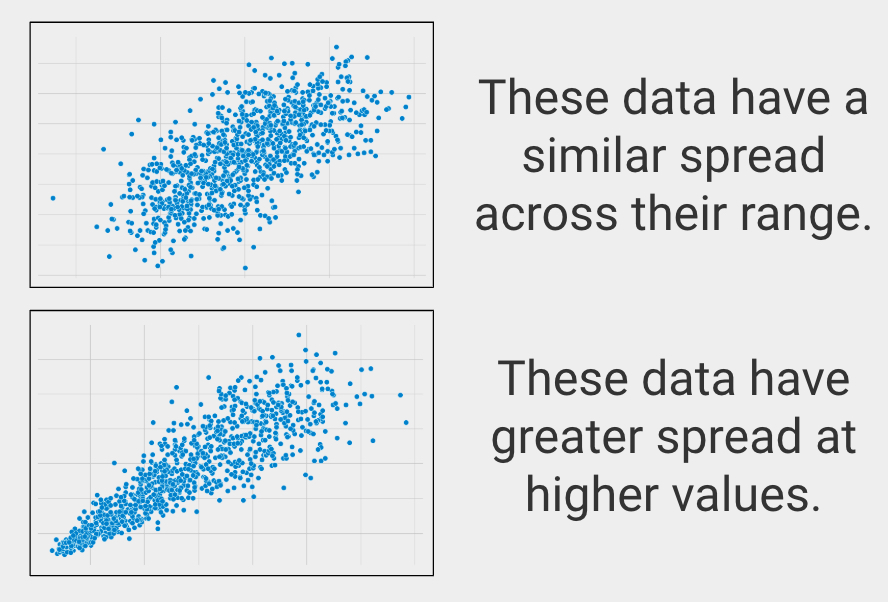
Podobný rozptyl v celém rozsahu
Ve statistice se tomu říká homoskedasticita, která popisuje, když mají proměnné podobný rozptyl ve svých rozsazích.
Normálnost reziduí
Slovem “rezidua” se označují hodnoty vzniklé odečtením očekávaných (nebo předpovídaných) závislých proměnných od skutečných hodnot. Rozložení těchto hodnot by mělo odpovídat normálnímu tvaru rozdělení (nebo zvonové křivce).
Splnění tohoto předpokladu zajišťuje, že výsledky regrese jsou stejně použitelné v celém rozpětí dat a že nedochází k systematickému zkreslení předpovědi.
Žádná multikolinearita
Multikolinearita označuje scénář, kdy jsou dvě nebo více nezávislých proměnných mezi sebou podstatně korelovány. Pokud je multikolinearita přítomna, regresní koeficienty a statistická významnost se stávají nestabilními a méně důvěryhodnými, ačkoli sama o sobě nemá vliv na to, jak dobře model odpovídá datům.
Kdy použít vícerozměrnou lineární regresi?
Vícerozměrnou vícenásobnou lineární regresi byste měli použít v následujícím případě:
- Chcete použít jednu proměnnou k predikci více jiných proměnných nebo chcete kvantifikovat číselný vztah mezi nimi
- Proměnné, které chcete predikovat (vaše závislá proměnná), jsou spojité
- Máte více než jednu nezávislou proměnnou, nebo jednu proměnnou, kterou používáte jako prediktor
- Nemáte opakovaná měření ze stejné jednotky pozorování
- Máte více než jednu závisle proměnnou
Ujasníme si je, abyste věděli, kdy použít vícerozměrnou lineární regresi.
Předpověď
Hledáte statistický test pro předpověď jedné proměnné pomocí jiné. Jedná se o otázku týkající se predikce. Mezi další typy analýz patří zkoumání síly vztahu mezi dvěma proměnnými (korelace) nebo zkoumání rozdílů mezi skupinami (rozdíl).
Spojitá závislá proměnná
Proměnná, kterou chcete předpovědět, musí být spojitá. Spojitá znamená, že proměnná, která vás zajímá, může nabývat v podstatě libovolných hodnot, například srdeční tep, výška, hmotnost, počet zmrzlinových tyčinek, které dokážete sníst za 1 minutu, atd.
Mezi typy dat, která NEJSOU spojitá, patří uspořádaná data (například umístění v závodě, žebříčky nejlepších firem atd.), kategoriální data (pohlaví, barva očí, rasa atd.) nebo binární data (koupil si výrobek nebo ne, má nemoc nebo ne atd.).
Pokud je vaše závislá proměnná binární, měli byste použít vícenásobnou logistickou regresi, a pokud je vaše závislá proměnná kategoriální, pak byste měli použít vícenásobnou logistickou regresi nebo lineární diskriminační analýzu.
Více než jedna nezávislá proměnná
Vícerozměrná vícenásobná lineární regrese se používá v případě, že pro každou jednotku pozorování existuje jedna nebo více predikčních proměnných s více hodnotami.
Žádná opakovaná měření
Tato metoda je vhodná pro scénář, kdy pro každou jednotku pozorování existuje pouze jedno pozorování. Jednotka pozorování je to, co tvoří “datový bod”, například obchod, zákazník, město atd…
Pokud máte jednu nebo více nezávislých proměnných, ale jsou měřeny pro stejnou skupinu ve více časových bodech, pak byste měli použít model smíšených efektů.
Více než jedna závislá proměnná
Chcete-li spustit vícerozměrnou vícenásobnou lineární regresi, měli byste mít více než jednu závislou proměnnou neboli proměnnou, kterou se snažíte předpovídat.
Pokud předpovídáte pouze jednu proměnnou, měli byste použít vícenásobnou lineární regresi.
Příklad vícerozměrné vícenásobné lineární regrese
Návislá proměnná 1:
Závislá proměnná 2: Návštěvnost zákazníků
Nezávislá proměnná 1: Nezávislá proměnná 2: Počet obyvatel města
Nulová hypotéza, což je statistický žargon pro to, co by se stalo, kdyby léčba nic neudělala, je, že neexistuje žádný vztah mezi výdaji na reklamu a reklamními dolary nebo počtem obyvatel podle měst. Náš test posoudí pravděpodobnost pravdivosti této hypotézy.
Shromáždíme naše data a po ujištění, že jsou splněny předpoklady lineární regrese, provedeme analýzu.
Tato analýza fakticky provádí vícenásobnou lineární regresi dvakrát s použitím obou závislých proměnných. Když tedy provedeme tuto analýzu, získáme beta koeficienty a p-hodnoty pro každý člen v modelu “tržby” a v modelu “návštěvnost zákazníků”. Pro každý lineární regresní model budete mít jeden koeficient beta, který se rovná průsečíku lineární regresní přímky (často se označuje nulou jako β0). To je jednoduše místo, kde regresní přímka protíná osu y, pokud byste svá data vynesli do grafu. V případě vícenásobné lineární regrese existují navíc ještě dva další koeficienty beta (β1, β2 atd.), které představují vztah mezi nezávislou a závislou proměnnou.
Tyto další koeficienty beta jsou klíčem k pochopení číselného vztahu mezi vašimi proměnnými. V podstatě se očekává, že při každém jednotkovém (hodnota 1) zvýšení dané nezávislé proměnné se vaše závislá proměnná změní o hodnotu koeficientu beta spojeného s touto nezávislou proměnnou (při zachování ostatních nezávislých proměnných na konstantní úrovni).
Hodnota p spojená s těmito dodatečnými hodnotami beta je šance, že uvidíme naše výsledky za předpokladu, že mezi danou proměnnou a příjmy ve skutečnosti neexistuje žádný vztah. Hodnota p menší nebo rovna 0,05 znamená, že náš výsledek je statisticky významný a můžeme věřit, že rozdíl není způsoben pouze náhodou. K získání celkové p-hodnoty pro model a jednotlivých p-hodnot, které představují vliv proměnných napříč oběma modely, se často používá MANOVA.
Při této analýze navíc získáme hodnotu R-Squared (R2). Tato hodnota se může pohybovat v rozmezí 0-1 a představuje, jak dobře lineární regresní přímka odpovídá datovým bodům. Čím vyšší je R2, tím lépe váš model odpovídá vašim datům.
Často kladené otázky
Q: Jaký je rozdíl mezi vícerozměrnou vícenásobnou lineární regresí a vícenásobným spuštěním lineární regrese?
A: Jsou koncepčně podobné, protože jednotlivé koeficienty modelu budou v obou scénářích stejné. Podstatný rozdíl však spočívá v tom, že testy významnosti a intervaly spolehlivosti pro vícerozměrnou lineární regresi zohledňují více závislých proměnných.
Q: Jak spustit vícerozměrnou vícenásobnou lineární regresi v SPSS, R, SAS nebo STATA?
A: Tento zdroj je zaměřen na to, aby vám pomohl vybrat vždy správnou statistickou metodu. K dispozici je mnoho zdrojů, které vám pomohou zjistit, jak tuto metodu spustit s vašimi daty:
Článek o R: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/
Nápověda!”
Pokud stále nemůžete na něco přijít, neváhejte se na nás obrátit.
.