Druck-, Volumen- und Temperaturverhältnisse in realen Gasen
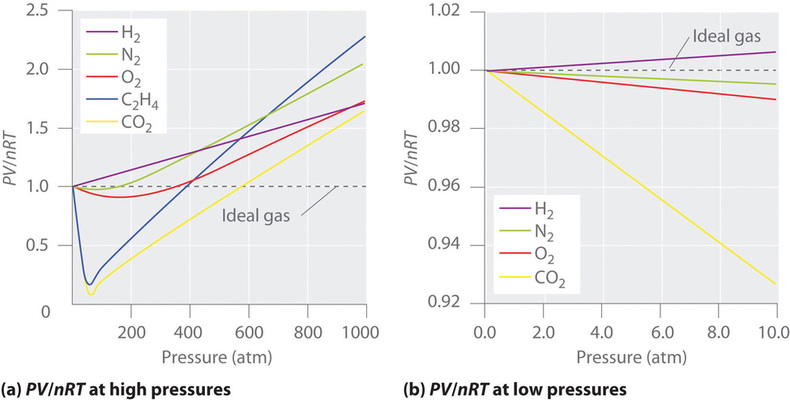
Für ein ideales Gas ergibt eine Darstellung von \(PV/nRT\) gegen \(P\) eine horizontale Linie mit einem Schnittpunkt von 1 auf der Achse \(PV/nRT\). Reale Gase zeigen jedoch erhebliche Abweichungen von dem für ein ideales Gas erwarteten Verhalten, insbesondere bei hohen Drücken (Abbildung \(\PageIndex{1a}\)). Nur bei relativ niedrigen Drücken (weniger als 1 atm) nähern sich reale Gase dem idealen Gasverhalten an (Abbildung \(\PageIndex{1b}\)).
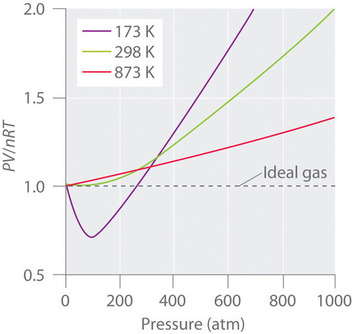
Reale Gase nähern sich dem idealen Gasverhalten auch bei höheren Temperaturen stärker an, wie in Abbildung \(\PageIndex{2}\) für \(N_2\) gezeigt. Warum verhalten sich reale Gase bei hohen Drücken und niedrigen Temperaturen so anders als ideale Gase? Unter diesen Bedingungen sind die beiden grundlegenden Annahmen, die dem idealen Gasgesetz zugrunde liegen – nämlich dass die Gasmoleküle ein vernachlässigbares Volumen haben und dass die zwischenmolekularen Wechselwirkungen vernachlässigbar sind – nicht mehr gültig.
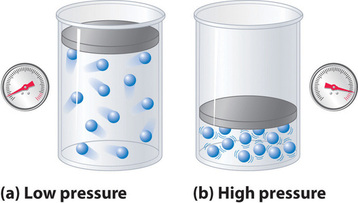
Da man davon ausgeht, dass die Moleküle eines idealen Gases ein Volumen von Null haben, ist das ihnen für die Bewegung zur Verfügung stehende Volumen immer gleich dem Volumen des Behälters. Im Gegensatz dazu haben die Moleküle eines realen Gases kleine, aber messbare Volumina. Bei niedrigem Druck sind die Gasmoleküle relativ weit voneinander entfernt, aber wenn der Druck des Gases steigt, werden die intermolekularen Abstände immer kleiner (Abbildung \(\PageIndex{3}\)). Dies hat zur Folge, dass das von den Molekülen eingenommene Volumen im Vergleich zum Volumen des Behälters signifikant wird. Folglich ist das vom Gas eingenommene Gesamtvolumen größer als das nach dem idealen Gasgesetz vorhergesagte Volumen. Daher ist bei sehr hohen Drücken der experimentell gemessene Wert von PV/nRT größer als der durch das ideale Gasgesetz vorhergesagte Wert.
Außerdem werden alle Moleküle durch eine Kombination von Kräften zueinander hingezogen. Diese Kräfte sind besonders wichtig für Gase bei niedrigen Temperaturen und hohem Druck, wo die zwischenmolekularen Abstände kürzer sind. Die Anziehungskräfte zwischen den Molekülen verringern die Zahl der Zusammenstöße mit der Behälterwand, ein Effekt, der umso ausgeprägter ist, je größer die Zahl der anziehenden Wechselwirkungen ist. Da der durchschnittliche Abstand zwischen den Molekülen abnimmt, verringert sich der vom Gas auf die Behälterwand ausgeübte Druck, und der beobachtete Druck ist geringer als erwartet (Abbildung \(\PageIndex{4}\)). Wie in Abbildung \(\PageIndex{2}\) zu sehen ist, ist das Verhältnis von \(PV/nRT\) bei niedrigen Temperaturen niedriger als für ein ideales Gas vorhergesagt, ein Effekt, der besonders bei komplexen Gasen und bei einfachen Gasen bei niedrigen Temperaturen deutlich wird. Bei sehr hohen Drücken überwiegt der Effekt des Molekularvolumens ungleich Null. Die Konkurrenz zwischen diesen Effekten ist für das Minimum verantwortlich, das im Diagramm \(PV/nRT\) gegen \(P\) für viele Gase beobachtet wird.
Das Molekülvolumen ungleich Null führt dazu, dass das tatsächliche Volumen bei hohen Drücken größer ist als vorhergesagt; intermolekulare Anziehungskräfte führen dazu, dass der Druck geringer ist als vorhergesagt.
Bei hohen Temperaturen haben die Moleküle genügend kinetische Energie, um intermolekulare Anziehungskräfte zu überwinden, und die Effekte des Molekülvolumens ungleich Null überwiegen. Umgekehrt nimmt die kinetische Energie der Gasmoleküle mit sinkender Temperatur ab. Schließlich wird ein Punkt erreicht, an dem die Moleküle die zwischenmolekularen Anziehungskräfte nicht mehr überwinden können, und das Gas verflüssigt sich (kondensiert zu einer Flüssigkeit).