Graphen in Python

Ursprünge der Graphentheorie

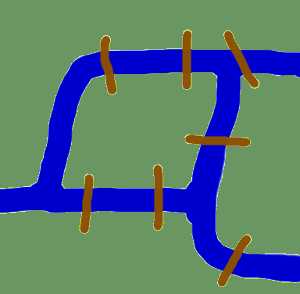Bevor wir uns mit den eigentlichen Implementierungen von Graphen in Python beschäftigen und bevor wir mit der Einführung von Python-Modulen beginnen, die sich mit Graphen beschäftigen, wollen wir uns den Ursprüngen der Graphentheorie widmen.
Die Ursprünge führen uns zurück in das Künigsberg des 18. Königsberg war damals eine Stadt in Preußen. Der Fluss Pregel floss durch die Stadt und bildete zwei Inseln. Die Stadt und die Inseln waren durch sieben Brücken miteinander verbunden (siehe Abbildung). Die Einwohner der Stadt bewegte die Frage, ob es möglich sei, einen Spaziergang durch die Stadt zu machen, indem man jeden Stadtteil besucht und jede Brücke nur einmal überquert? Jede Brücke muss vollständig überquert worden sein, d. h. es ist nicht erlaubt, eine Brücke zur Hälfte zu betreten und dann umzudrehen und die andere Hälfte von der anderen Seite aus zu überqueren. Leonhard Euler löste das Problem im Jahr 1735, indem er bewies, dass dies nicht möglich ist. Er fand heraus, dass die Wahl des Weges innerhalb jedes Landgebiets irrelevant ist und dass es nur auf die Reihenfolge ankommt, in der die Brücken überquert werden. Er hatte eine Abstraktion des Problems formuliert, indem er unnötige Fakten eliminierte und sich auf die Landgebiete und die sie verbindenden Brücken konzentrierte. Auf diese Weise schuf er die Grundlagen der Graphentheorie. Wenn wir eine “Landfläche” als Scheitelpunkt und jede Brücke als Kante betrachten, haben wir das Problem auf einen Graphen “reduziert”.

Einführung in die Graphentheorie mit Python

Bevor wir uns mit möglichen Python-Darstellungen von Graphen befassen, wollen wir einige allgemeine Definitionen von Graphen und ihren Bestandteilen vorstellen.
Ein “Graph “1 in der Mathematik und Informatik besteht aus “Knoten”, auch “Vertices” genannt, die miteinander verbunden sein können oder auch nicht. In unserer Abbildung – die eine bildliche Darstellung eines Graphen ist – ist der Knoten “a” mit dem Knoten “c” verbunden, aber “a” ist nicht mit “b” verbunden. Die Verbindungslinie zwischen zwei Knoten wird als Kante bezeichnet. Wenn die Kanten zwischen den Knoten ungerichtet sind, wird der Graph als ungerichteter Graph bezeichnet. Wenn eine Kante von einem Knoten zu einem anderen gerichtet ist, nennt man den Graphen einen gerichteten Graphen. Eine gerichtete Kante wird als Bogen bezeichnet.
Auch wenn Graphen sehr theoretisch aussehen, können viele praktische Probleme durch Graphen dargestellt werden. Sie werden häufig zur Modellierung von Problemen oder Situationen in der Physik, Biologie, Psychologie und vor allem in der Informatik verwendet. In der Informatik werden Graphen zur Darstellung von Kommunikationsnetzen, der Datenorganisation, von Rechengeräten und des Rechenflusses verwendet,

Im letzteren Fall werden sie zur Darstellung der Datenorganisation, wie dem Dateisystem eines Betriebssystems, oder von Kommunikationsnetzen verwendet. Die Linkstruktur von Webseiten kann auch als Graph betrachtet werden, d.h. als gerichteter Graph, da ein Link eine gerichtete Kante oder ein Bogen ist.
Python hat keinen eingebauten Datentyp oder Klasse für Graphen, aber es ist einfach, sie in Python zu implementieren. Ein Datentyp ist ideal für die Darstellung von Graphen in Python, nämlich Dictionaries. Der Graph in unserer Abbildung kann auf folgende Weise implementiert werden:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Die Schlüssel des obigen Wörterbuchs sind die Knoten unseres Graphen. Die zugehörigen Werte sind Listen mit den Knoten, die durch eine Kante verbunden sind. Es gibt keinen einfacheren und eleganteren Weg, einen Graphen darzustellen.
Eine Kante kann als 2-Tupel mit Knoten als Elementen betrachtet werden, z.B. (“a”, “b”)
Funktion zur Erzeugung der Liste aller Kanten:Dieser Code erzeugt die folgende Ausgabe, wenn er mit dem zuvor definierten Graphen-Wörterbuch kombiniert wird:

 $ python3 graph_simple.py 

Wie wir sehen können, gibt es keine Kante, die den Knoten “f” enthält. “f” ist ein isolierter Knoten unseres Graphen.
Die folgende Python-Funktion berechnet die isolierten Knoten eines gegebenen Graphen:Wenn wir diese Funktion mit unserem Graphen aufrufen, wird eine Liste mit “f” zurückgegeben:

Graphen als Python-Klasse

Bevor wir mit dem Schreiben von Funktionen für Graphen fortfahren, machen wir einen ersten Versuch mit der Implementierung einer Python-Graphenklasse. Wenn man sich das folgende Listing unserer Klasse anschaut, kann man in der __init__-Methode sehen, dass wir ein Dictionary “self.__graph_dict” zum Speichern der Scheitelpunkte und der dazugehörigen Nachbarscheitelpunkte verwenden.
Wenn man dieses Modul eigenständig startet, erhält man folgendes Ergebnis:

Pfade in Graphen

Wir wollen nun den kürzesten Pfad von einem Knoten zu einem anderen Knoten finden. Bevor wir zum Python-Code für dieses Problem kommen, müssen wir einige formale Definitionen vorstellen.
Nachbarn:
Zwei Knoten sind benachbart, wenn sie beide auf einer gemeinsamen Kante liegen.
Pfad in einem ungerichteten Graphen:
Ein Pfad in einem ungerichteten Graphen ist eine Folge von Knoten P = ( v1, v2, …, vn ) ∈ V x V x … x V, so dass vi an v{i+1} für 1 ≤ i < n angrenzt. Ein solcher Pfad P wird als Pfad der Länge n von v1 bis vn bezeichnet.
Ein einfacher Pfad:
Ein Pfad ohne sich wiederholende Knoten wird als einfacher Pfad bezeichnet.

Beispiel:
(a, c, e) ist ein einfacher Pfad in unserem Graphen, ebenso wie (a,c,e,b). (a,c,e,b,c,d) ist ein Pfad, aber kein einfacher Pfad, weil der Knoten c zweimal vorkommt.
Die folgende Methode findet einen Pfad von einem Startpunkt zu einem Endpunkt:Wenn wir unsere Graphklasse inklusive der find_path-Methode als “graphs.py” speichern, können wir die Arbeitsweise unserer find_path-Funktion überprüfen:Das Ergebnis des vorherigen Programms sieht so aus:
Die Methode find_all_paths findet alle Pfade zwischen einem Start-Eckpunkt und einem End-Eckpunkt:Wir haben unseren Beispielgraphen leicht verändert, indem wir Kanten von “a” nach “f” und von “f” nach “d” hinzugefügt haben, um die zuvor definierte Methode zu testen:Das Ergebnis sieht so aus:

Grad

Der Grad eines Knotens v in einem Graphen ist die Anzahl der Kanten, die ihn verbinden, wobei Schleifen doppelt gezählt werden. Der Grad eines Knotens v wird mit deg(v) bezeichnet. Der maximale Grad eines Graphen G, bezeichnet mit Δ(G), und der minimale Grad eines Graphen, bezeichnet mit δ(G), sind der maximale und der minimale Grad seiner Scheitelpunkte.
In dem Graphen auf der rechten Seite ist der maximale Grad 5 am Knoten c und der minimale Grad 0, d.h. der isolierte Knoten f.
Wenn alle Grade in einem Graphen gleich sind, ist der Graph ein regulärer Graph.In einem regulären Graphen sind alle Grade gleich, so dass man vom Grad des Graphen sprechen kann.
Die Gradsummenformel (Handshaking-Lemma):
∑v &in; Vdeg(v) = 2 |E|
Das bedeutet, dass die Summe der Grade aller Scheitelpunkte gleich der Anzahl der Kanten multipliziert mit 2 ist.Wir können schließen, dass die Anzahl der Scheitelpunkte mit ungeradem Grad gerade sein muss. Diese Aussage ist als Handshaking-Lemma bekannt. Der Name “Handshaking-Lemma” stammt von einem populären mathematischen Problem: In einer beliebigen Gruppe von Personen ist die Anzahl der Personen, die einer ungeraden Anzahl von anderen Personen aus der Gruppe die Hand geschüttelt haben, gerade.
Die folgende Methode berechnet den Grad eines Scheitelpunkts:
Die folgende Methode berechnet eine Liste mit den isolierten Scheitelpunkten eines Graphen:Die Methoden Delta und Delta können verwendet werden, um den minimalen bzw. maximalen Grad eines Scheitelpunkts zu berechnen:

Gradfolge

Die Gradfolge eines ungerichteten Graphen ist definiert als die Folge seiner Knotengrade in nicht-aufsteigender Reihenfolge.
Die folgende Methode gibt ein Tupel mit der Gradfolge des Instanzgraphen zurück:
Die Gradfolge unseres Beispielgraphen ist die folgende Folge von ganzen Zahlen: (5,2,1,1,1,0).

Isomorphe Graphen haben die gleiche Gradfolge. Zwei Graphen mit der gleichen Gradfolge sind aber nicht unbedingt isomorph.
Es stellt sich die Frage, ob eine gegebene Gradfolge durch einen einfachen Graphen realisiert werden kann. Das Erdös-Gallai-Theorem besagt, dass eine nicht-steigende Folge von n Zahlen di (füri = 1, …, n) dann und nur dann die Gradfolge eines einfachen Graphen ist, wenn die Summe der Folge gerade ist und die folgende Bedingung erfüllt ist:

Umsetzung des Erdös-Gallai-Satzes

Unsere Graphenklasse – siehe weiter unten für eine vollständige Auflistung – enthält eine Methode “erdoes_gallai”, die entscheidet, ob eine Folge den Erdös-Gallai-Satz erfüllt. Zunächst wird geprüft, ob die Summe der Elemente der Folge ungerade ist. Ist dies der Fall, gibt die Funktion False zurück, da das Erdös-Gallai-Theorem nicht mehr erfüllt werden kann. Danach prüfen wir mit der statischen Methode is_degree_sequence, ob die Eingabesequenz eine Gradsequenz ist, d.h. ob die Elemente der Sequenz nicht aufsteigend sind. Dies ist eigentlich überflüssig, da die Eingabe eine Gradfolge sein soll, also kann man diese Prüfung aus Effizienzgründen weglassen. Nun prüfen wir im Körper der zweiten if-Anweisung, ob die Ungleichung des Theorems erfüllt ist:
Version ohne die überflüssige Gradfolgeprüfung:

Graphendichte

Die Graphendichte ist definiert als das Verhältnis zwischen der Anzahl der Kanten eines gegebenen Graphen und der Gesamtzahl der Kanten, die der Graph haben könnte. Mit anderen Worten: Sie misst, wie nahe ein gegebener Graph an einem vollständigen Graphen ist.
Die maximale Dichte ist 1, wenn ein Graph vollständig ist. Das ist klar, weil die maximale Anzahl der Kanten in einem Graphen von den Eckpunkten abhängt und berechnet werden kann als:
max. Anzahl der Kanten = ½ * |V| * ( |V| – 1 ).
Die minimale Dichte ist dagegen 0, wenn der Graph keine Kanten hat, d.h. es ist ein isolierter Graph.
Für ungerichtete einfache Graphen ist die Graphendichte wie folgt definiert: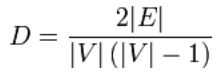

Ein dichter Graph ist ein Graph, bei dem die Anzahl der Kanten nahe der maximalen Kantenanzahl liegt. Ein Graph, der nur wenige Kanten aufweist, wird als spärlicher Graph bezeichnet. Die Definition für diese beiden Begriffe ist nicht sehr scharf, d.h. es gibt keine kleinste Obergrenze (Supremum) für einen spärlichen Graphen und keine größte Untergrenze (Infimum) für die Definition eines dichten Graphen.
Die präziseste mathematische Notation verwendet die große O-Notation:
Sparse Graph:
Dichter Graph:
Ein dichter Graph ist ein Graph G = (V, E), in dem |E| = Θ(|V|2).

“Dichte” ist eine Methode unserer Klasse, um die Dichte eines Graphen zu berechnen:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Wir können diese Methode mit dem folgenden Skript testen. Ein vollständiger Graph hat eine Dichte von 1 und ein isolierter Graph hat eine Dichte von 0, wie wir aus den Ergebnissen des vorherigen Testskripts ersehen können:

$ python test_density.py 0.4666666666671.00.0

Verbundene Graphen

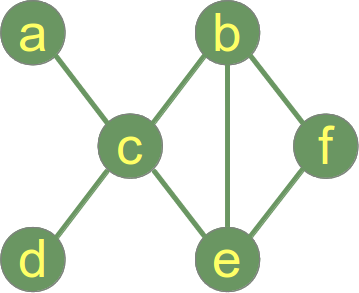Ein Graph wird als verbunden bezeichnet, wenn jedes Paar von Eckpunkten im Graphen verbunden ist. Der Beispielgraph auf der rechten Seite ist ein zusammenhängender Graph.
Es ist möglich, mit einem einfachen Algorithmus zu bestimmen, ob ein Graph zusammenhängend ist:

1. Wählen Sie einen beliebigen Knoten x des Graphen G als Ausgangspunkt
2. Bestimmen Sie die Menge A aller Knoten, die von x aus erreicht werden können.
3. Ist A gleich der Menge der Knoten von G, so ist der Graph verbunden; andernfalls ist er unverbunden.

Wir implementieren eine Methode is_connected, um zu prüfen, ob ein Graph ein verbundener Graph ist. Dabei legen wir keinen Wert auf Effizienz, sondern auf Lesbarkeit.
Wenn Sie diese Methode zu unserer Graphklasse hinzufügen, können wir sie mit dem folgenden Skript testen. Angenommen, Sie speichern die Graphklasse als graph2.py:
Eine zusammenhängende Komponente ist ein maximal zusammenhängender Untergraph von G. Jeder Knoten gehört zu genau einer zusammenhängenden Komponente, ebenso wie jede Kante.

Distanz und Durchmesser eines Graphen

Die Distanz “dist” zwischen zwei Knoten in einem Graphen ist die Länge des kürzesten Pfades zwischen diesen Knoten. Bei der Berechnung des Abstands sind keine Rückwege, Umwege oder Schleifen erlaubt.
In unserem Beispielgraphen rechts ist der Abstand zwischen dem Scheitelpunkt a und dem Scheitelpunkt f 3, d.h. dist(a,f) = 3, weil der kürzeste Weg über die Scheitelpunkte c und e (oder alternativ c und b) führt.
Die Exzentrizität eines Scheitelpunkts s eines Graphen g ist der maximale Abstand zu jedem anderen Scheitelpunkt des Graphen:
e(s) = max( { dist(s,v) | v ∈ V })
(V ist die Menge aller Scheitelpunkte von g)
Der Durchmesser d eines Graphen ist definiert als die maximale Exzentrizität eines beliebigen Scheitelpunkts im Graphen. Das bedeutet, dass der Durchmesser die Länge des kürzesten Weges zwischen den am weitesten entfernten Knoten ist. Um den Durchmesser eines Graphen zu bestimmen, muss zunächst der kürzeste Weg zwischen den einzelnen Knotenpaaren ermittelt werden. Die größte Länge eines dieser Pfade ist der Durchmesser des Graphen.

Wir können in unserem Beispielgraphen direkt sehen, dass der Durchmesser 3 ist, weil die minimale Länge zwischen a und f 3 ist und es kein anderes Paar von Knoten mit einem längeren Pfad gibt.
Die folgende Methode implementiert einen Algorithmus zur Berechnung des Durchmessers. Wir können den Durchmesser unseres Beispielgraphen mit dem folgenden Skript berechnen, wobei wir wieder davon ausgehen, dass unsere komplette Graphklasse als graph2.py gespeichert ist:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Es wird den Wert 3 ausgeben.

Die komplette Python-Graphklasse

Im folgenden Python-Code finden Sie das komplette Python-Klassenmodul mit allen besprochenen Methoden:graph2.py

Baum / Wald

Ein Baum ist ein ungerichteter Graph, der keine Zyklen enthält. Das bedeutet, dass zwei beliebige Eckpunkte des Graphen durch genau einen einfachen Pfad verbunden sind.
Ein Wald ist eine disjunkte Vereinigung von Bäumen. Im Gegensatz zu Wäldern in der Natur kann ein Wald in der Graphentheorie aus einem einzigen Baum bestehen!
Ein Graph mit einem Scheitelpunkt und keiner Kante ist ein Baum (und ein Wald).
Ein Beispiel für einen Baum: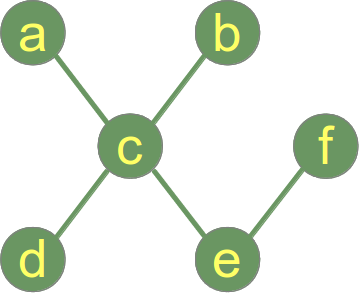

Während das vorherige Beispiel einen Graphen zeigt, der ein Baum und ein Wald ist, zeigt das folgende Bild einen Graphen, der aus zwei Bäumen besteht, d. h. der Graph ist ein Baum, aber ein Wald.d.h. der Graph ist ein Wald, aber kein Baum:

Übersicht über Wälder:

Mit einem Scheitelpunkt:

Waldgraphen mit zwei Scheitelpunkten:

Waldgraphen mit drei Scheitelpunkten:

Spannbaum

Ein Spannbaum T eines zusammenhängenden, ungerichteten Graphen G ist ein Teilgraph G’ von G, der ein Baum ist, und G’ enthält alle Scheitelpunkte und eine Teilmenge der Kanten von G. G’ enthält alle Kanten von G, wenn G ein Baumgraph ist. Informell ist ein übergreifender Baum von G eine Auswahl von Kanten von G, die einen Baum bilden, der jeden Scheitelpunkt umspannt. Das heißt, jeder Knoten liegt in dem Baum, aber es sind keine Zyklen (oder Schleifen) enthalten.
Beispiel:
Ein vollständig zusammenhängender Graph: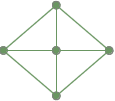

Zwei überspannende Bäume aus dem vorherigen vollständig zusammenhängenden Graph: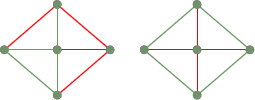

Hamiltonsches Spiel

Ein Hamiltonscher Pfad ist ein Pfad in einem ungerichteten oder gerichteten Graphen, der jeden Vertex genau einmal besucht. Ein Hamiltonscher Zyklus (oder Schaltkreis) ist ein Hamiltonscher Pfad, der ein Zyklus ist.
Hinweis für Informatiker: Im Allgemeinen ist es nicht möglich, festzustellen, ob solche Pfade oder Zyklen in beliebigen Graphen existieren, da das Hamilton-Pfad-Problem nachweislich NP-komplett ist.
Es ist nach William Rowan Hamilton benannt, der das sogenannte “Ikosianische Spiel” oder Hamiltons Rätsel erfand, bei dem es darum geht, einen Hamilton-Zyklus im Kantengraphen des Dodekaeders zu finden. Hamilton löste dieses Problem mit Hilfe der Ikosianischen Rechnung, einer algebraischen Struktur auf der Grundlage von Einheitswurzeln, die viele Ähnlichkeiten mit den ebenfalls von ihm erfundenen Quaternionen aufweist.

Komplettes Listing der Graph-Klasse

Wir können diese Graph-Klasse mit dem folgenden Programm testen:Wenn wir dieses Programm starten, erhalten wir folgende Ausgabe:
Fußnoten:
1 Die in der Graphentheorie (und in diesem Kapitel unseres Python-Tutorials) untersuchten Graphen sind nicht mit den Graphen von Funktionen zu verwechseln
2 Ein Singleton ist eine Menge, die genau ein Element enthält.
Credits:
Narayana Chikkam, nchikkam(at)gmail(dot)com, hat uns auf einen Indexfehler in der Methode “erdoes_gallai” hingewiesen. Herzlichen Dank, Narayana!