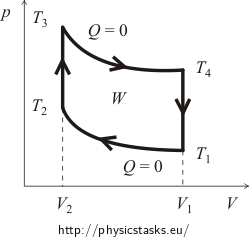
Zu Beginn ist es in der Regel notwendig, sich ein Bild vom pV-Diagramm des Zyklus zu machen. Dazu werden wir die Kurven der isochoren und adiabatischen Prozesse nachzeichnen. Das ungefähre Diagramm des Otto-Zyklus ist in der folgenden Abbildung dargestellt.

Der Wirkungsgrad η des Zyklus ist definiert als

\

wobei W die vom Gas während eines Zyklus geleistete Arbeit abzüglich der von den äußeren Kräften geleisteten Arbeit ist (im Diagramm wird sie durch die Fläche des durch die Linien des Zyklus definierten Bereichs dargestellt!) und Qsup ist die dem System während des Zyklus zugeführte Wärme.

Die Arbeit W kann anhand der Beziehung zwischen Druck und Volumen während einer adiabatischen Expansion und Kompression berechnet werden (die während eines isochoren Prozesses geleistete Arbeit ist natürlich Null). Bei dieser Aufgabe ist es jedoch besser, die Tatsache zu nutzen, dass die Gesamtänderung der inneren Energie pro Zyklus gleich Null sein muss (wir kehren in den gleichen Zustand wie zu Beginn zurück, daher bleiben die Temperatur und somit die innere Energie gleich!) Nach dem Ersten Hauptsatz der Thermodynamik kann die vom Gas geleistete Arbeit als Differenz zwischen der zugeführten Wärme Qsup und der abgegebenen Wärme Qrel ausgedrückt werden. Die Formel für den Wirkungsgrad des Kreislaufs lautet also:

\

Zunächst wird die zugeführte Wärme Qsup berechnet. Es ist klar, dass während des adiabatischen Prozesses kein Wärmeaustausch stattfindet und während der isochoren Abkühlung die Wärme freigesetzt wird. Das bedeutet, dass die Wärme nur während der isochoren Erwärmung von der Temperatur T2 auf die Temperatur T3 zugeführt wird. Die Menge dieser Wärme kann durch die Variablen der Stoffmenge n des Gases und seiner molaren Wärmekapazität CV wie folgt ausgedrückt werden:

\

Wir werden die Menge der freigesetzten Wärme Qrel auf die gleiche Weise ausdrücken. Wir wissen bereits, dass die Wärme nur während der isochoren Abkühlung von der Temperatur T4 zurück auf die Anfangstemperatur T1 freigesetzt wird. Es gilt:

\

Setzen wir nun diese Formeln in die Formel für den Wirkungsgrad des Kreislaufs ein, so erhalten wir sofort:

\

Nun müssen wir die Temperaturunterschiede mit Hilfe des gegebenen Kompressionsverhältnisses

\

und der Poissonzahl κ ausdrücken.

Dazu verwenden wir die Gleichung für ein ideales Gas, das einen adiabatischen Prozess durchläuft (das Poissonsche Gesetz) pVκ = C = konst, wobei C eine Konstante ist. Nun berechnen wir den Druck aus der Zustandsgleichung eines idealen Gases

, den wir in das Poissonsche Gesetz einsetzen. Nun übertragen wir die Konstanten (C und K) auf eine Seite

\

Nun wenden wir dieses Poissonsche Gesetz für beide adiabatischen Prozesse an. Für die adiabatische Expansion erhalten wir die Beziehung

\

Und für die adiabatische Kompression erhalten wir

\

Nun subtrahieren wir die zweite Gleichung von der ersten und faktorisieren V1κ – 1 auf der einen und V2κ – 1 auf der anderen Seite. Wir erhalten:

\ \

Wir sehen, dass es uns tatsächlich gelungen ist, die Temperaturunterschiede mit den gegebenen Werten auszudrücken. Nun setzen wir diese Beziehung in die Formel für den Wirkungsgrad ein und erhalten die endgültige Gleichung:

\ \