Im vorherigen Kapitel haben wir über Latches gesprochen. Das sind die Grundbausteine von Flipflops. Wir können Flipflops auf zwei Arten implementieren.
Bei der ersten Methode werden zwei Latches so kaskadiert, dass das erste Latch bei jedem positiven Taktimpuls und das zweite Latch bei jedem negativen Taktimpuls aktiviert wird. So wird die Kombination dieser beiden Latches zu einem Flip-Flop.
Bei der zweiten Methode können wir das Flip-Flop, das flankenempfindlich ist, direkt implementieren. In diesem Kapitel werden wir die folgenden Flip-Flops mit der zweiten Methode besprechen.
- SR Flip-Flop
- D Flip-Flop
- JK Flip-Flop
- T Flip-Flop
SR Flip-Flop
SR Flip-Flop arbeitet nur mit positiven Taktübergängen oder negativen Taktübergängen. Das SR-Latch hingegen arbeitet mit einem Freigabesignal. Das Schaltbild eines SR-Flipflops ist in der folgenden Abbildung dargestellt.
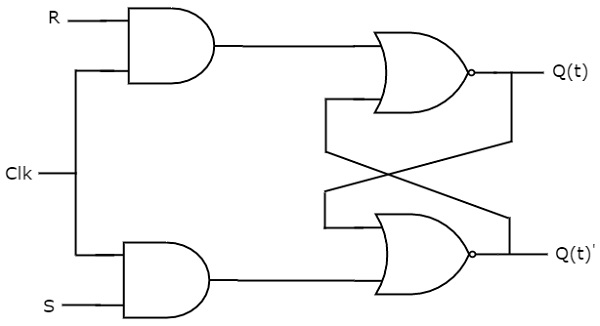
Diese Schaltung hat zwei Eingänge S & R und zwei Ausgänge Q(t) & Q(t)’. Die Funktionsweise des SR-Flipflops ist ähnlich wie beim SR-Latch. Allerdings wirkt sich dieses Flipflop nur auf die Ausgänge aus, wenn ein positiver Übergang des Taktsignals anstelle der aktiven Freigabe angelegt wird.
Die folgende Tabelle zeigt die Zustandstabelle des SR-Flipflops.
| S | R | Q(t + 1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | – |
Hier, Q(t) & Q(t + 1) sind jeweils der aktuelle Zustand & der nächste Zustand. Das SR-Flipflop kann also für eine dieser drei Funktionen wie Halten, Zurücksetzen & Setzen auf der Grundlage der Eingangsbedingungen verwendet werden, wenn ein positiver Übergang des Taktsignals angelegt wird. Die folgende Tabelle zeigt die charakteristische Tabelle des SR-Flipflops.
| Anwesende Eingänge | Anwesender Zustand | Nächster Zustand | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | x |
| 1 | 1 | 1 | x |
Unter Verwendung von drei variablen K-Map, können wir den vereinfachten Ausdruck für den nächsten Zustand, Q(t + 1), erhalten. Die dreivariable K-Map für den nächsten Zustand, Q(t + 1), ist in der folgenden Abbildung dargestellt.
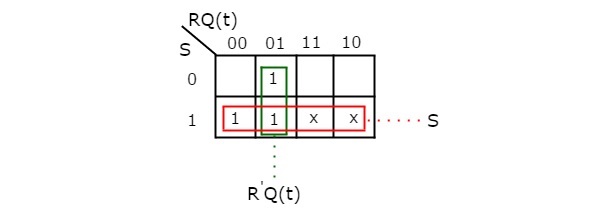
Die maximal möglichen Gruppierungen von benachbarten sind bereits in der Abbildung dargestellt. Daher lautet der vereinfachte Ausdruck für den nächsten Zustand Q(t + 1)
$Q\left ( t+1 \right )=S+{R}’Q\left ( t \right )$
D Flip-Flop
D Flip-Flop arbeitet nur mit positiven Taktübergängen oder negativen Taktübergängen. Ein D-Latch hingegen arbeitet mit einem Freigabesignal. Das heißt, der Ausgang des D-Flip-Flops ist unempfindlich gegenüber Änderungen am Eingang D, außer bei aktivem Übergang des Taktsignals. Das Schaltbild eines D-Flip-Flops ist in der folgenden Abbildung dargestellt.
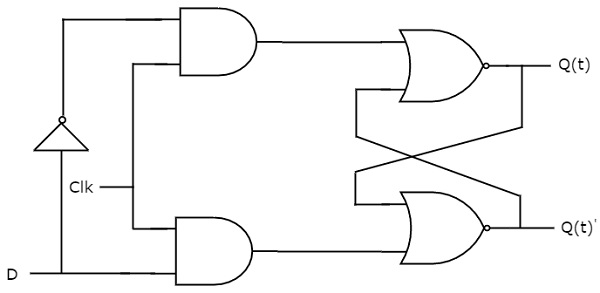
Diese Schaltung hat einen einzelnen Eingang D und zwei Ausgänge Q(t) & Q(t)’. Die Funktionsweise der D-Flip-Flop-Schaltung ist ähnlich wie die der D-Latch-Schaltung. Aber dieses Flipflop beeinflusst die Ausgänge nur, wenn ein positiver Übergang des Taktsignals anstelle der aktiven Freigabe angelegt wird.
Die folgende Tabelle zeigt die Zustandstabelle des D-Flipflops.
| D | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Daher, D-Flip-Flop immer die Information halten, die am Dateneingang D des früheren positiven Übergangs des Taktsignals vorhanden ist. Aus der obigen Zustandstabelle können wir die Gleichung für den nächsten Zustand direkt schreiben als
Q(t + 1) = D
Der nächste Zustand des D-Flipflops ist immer gleich dem Dateneingang D für jeden positiven Übergang des Taktsignals. Daher können D-Flip-Flops in Registern, Schieberegistern und einigen Zählern verwendet werden.
JK-Flip-Flop
JK-Flip-Flop ist die modifizierte Version von SR-Flip-Flop. Es arbeitet nur mit positiven Taktübergängen oder negativen Taktübergängen. Das Schaltbild eines JK-Flipflops ist in der folgenden Abbildung dargestellt.
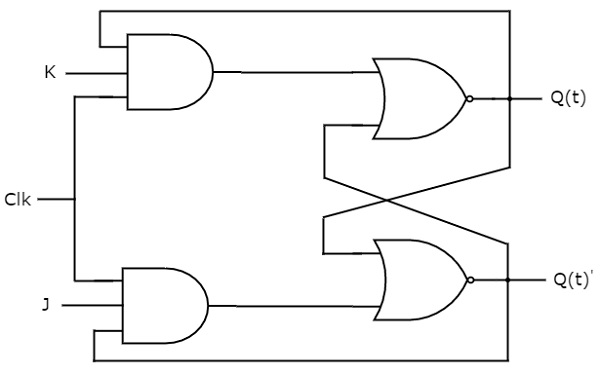
Diese Schaltung hat zwei Eingänge J & K und zwei Ausgänge Q(t) & Q(t)’. Die Funktionsweise von JK-Flip-Flop ist ähnlich wie die von SR-Flip-Flop. Hier haben wir die Eingänge des SR-Flipflops als S = J Q(t)’ und R = KQ(t) betrachtet, um das modifizierte SR-Flipflop für 4 Kombinationen von Eingängen zu verwenden.
Die folgende Tabelle zeigt die Zustandstabelle des JK-Flipflops.
| J | K | Q(t + 1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q(t)’ |
Hier, Q(t) & Q(t + 1) sind jeweils der aktuelle Zustand & der nächste Zustand. Das JK-Flipflop kann also für eine dieser vier Funktionen wie Halten, Zurücksetzen, Setzen & Komplement des gegenwärtigen Zustands auf der Grundlage der Eingangsbedingungen verwendet werden, wenn ein positiver Übergang des Taktsignals angelegt wird. Die folgende Tabelle zeigt die charakteristische Tabelle des JK-Flipflops.
| Anliegende Eingänge | Anliegender Zustand | Nächster Zustand | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Unter Verwendung von drei variablen K-Map, können wir den vereinfachten Ausdruck für den nächsten Zustand, Q(t + 1), erhalten. Die Drei-Variablen-K-Map für den nächsten Zustand Q(t + 1) ist in der folgenden Abbildung dargestellt.
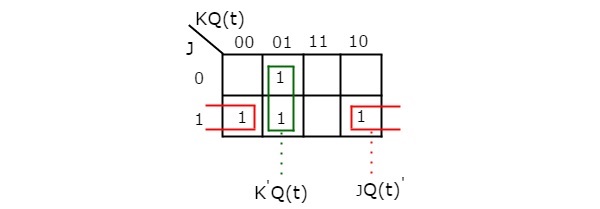
Die maximal möglichen Gruppierungen von benachbarten sind bereits in der Abbildung dargestellt. Daher ist der vereinfachte Ausdruck für den nächsten Zustand Q(t+1)
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}’+{K}’Q\left ( t \right )$$
T-Flip-Flop
T-Flip-Flop ist die vereinfachte Version von JK-Flip-Flop. Man erhält es, indem man denselben Eingang “T” an beide Eingänge des JK-Flipflops anschließt. Es arbeitet nur mit positiven oder negativen Taktübergängen. Das Schaltbild des T-Flipflops ist in der folgenden Abbildung dargestellt.
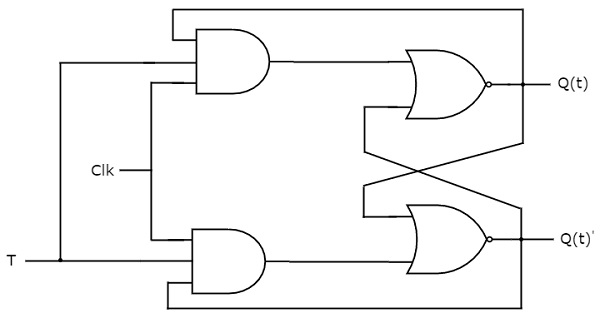
Diese Schaltung hat einen einzigen Eingang T und zwei Ausgänge Q(t) & Q(t)’. Die Funktionsweise des T-Flip-Flops ist dieselbe wie die des JK-Flip-Flops. Hier haben wir die Eingänge des JK-Flipflops als J = T und K = T betrachtet, um das modifizierte JK-Flipflop für 2 Kombinationen von Eingängen zu verwenden. Wir haben also die beiden anderen Kombinationen von J & K eliminiert, für die diese beiden Werte im T-Flipflop komplementär sind.
Die folgende Tabelle zeigt die Zustandstabelle des T-Flipflops.
| D | Q(t + 1) |
|---|---|
| 0 | Q(t) |
| 1 | Q(t)’ |
Hier, Q(t) & Q(t + 1) sind jeweils der aktuelle Zustand & der nächste Zustand. Das Flipflop T kann also für eine dieser beiden Funktionen verwendet werden, wie z. B. Halten, & Komplement des gegenwärtigen Zustands auf der Grundlage der Eingangsbedingungen, wenn ein positiver Übergang des Taktsignals angelegt wird. Die folgende Tabelle zeigt die charakteristische Tabelle des T-Flipflops.
| Eingänge | Anwesender Zustand | Nächster Zustand |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Aus der obigen charakteristischen Tabelle, können wir die nächste Zustandsgleichung direkt schreiben als
$$Q\left ( t+1 \right )={T}’Q\left ( t \right )+TQ{\left ( t \right )}’$$
$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
Der Ausgang von T Flip-flip-flop schaltet bei jedem positiven Übergang des Taktsignals immer um, wenn der Eingang T auf logisch High (1) bleibt. Daher kann T flip-flop in Zählern verwendet werden.
In diesem Kapitel haben wir verschiedene flip-flops implementiert, indem wir die Kreuzkopplung zwischen NOR-Gattern bereitgestellt haben. In ähnlicher Weise kann man diese Flipflops mit NAND-Gattern implementieren.