6.3 Belief Networks
Der Begriff der bedingten Unabhängigkeit kann verwendet werden, um eine prägnante Darstellung vieler Bereiche zu geben. Die Idee ist, dass es bei einer Zufallsvariablen X eine kleine Menge von Variablen geben kann, die den Wert der Variablen direkt in dem Sinne beeinflussen, dass X bei gegebenen Werten für die direkt beeinflussenden Variablen bedingungslos unabhängig von anderen Variablen ist. Die Menge der sich lokal auswirkenden Variablen wird als Markov-Decke bezeichnet. Diese Lokalität wird in einem Glaubensnetz ausgenutzt. Ein Glaubensnetzwerk ist ein gerichtetes Modell der bedingten Abhängigkeit zwischen einer Reihe von Zufallsvariablen. Die genaue Aussage über die bedingte Unabhängigkeit in einem Glaubensnetzwerk berücksichtigt die Direktionalität.
Um ein Glaubensnetzwerk zu definieren, beginnt man mit einer Menge von Zufallsvariablen, die alle Merkmale des Modells darstellen. Nehmen wir an, diese Variablen sind {X1,…,Xn}.Wählen Sie dann eine Gesamtordnung der Variablen, X1,…,Xn.
Die Kettenregel (Proposition 6.3) zeigt, wie man eine Konjunktion in bedingte Wahrscheinlichkeiten zerlegt:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Oder, in Form von Zufallsvariablen und Wahrscheinlichkeitsverteilungen,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Definieren Sie die Eltern der Zufallsvariablen Xi, geschriebenparents(Xi), als eine minimale Menge von Vorgängern von Xi in der Gesamtordnung, so dass die anderen Vorgänger von Xi beiparents(Xi) bedingt unabhängig von Xi sind. Das heißt, Eltern(Xi) ⊆{X1,…,Xi-1}, so dass
P(Xi|Xi-1…X1) = P(Xi|Eltern(Xi)).
Wenn mehr als eine minimale Menge existiert, kann jede minimale Menge als Eltern gewählt werden. Es kann nur dann mehr als eine minimale Menge geben, wenn einige der Vorgänger deterministische Funktionen der anderen sind.
Wir können die Kettenregel und die Definition der Eltern zusammenfügen, was
P(X1, X2,—, Xn) = ∏i=1n P(Xi|Eltern(Xi)).
Die Wahrscheinlichkeit über alle Variablen, P(X1, X2,—,Xn), wird die gemeinsame Wahrscheinlichkeitsverteilung genannt. Ein Glaubensnetzwerk definiert eine Faktorisierung der gemeinsamen Wahrscheinlichkeitsverteilung, wobei die bedingten Wahrscheinlichkeiten Faktoren bilden, die miteinander multipliziert werden.
Ein Glaubensnetzwerk, auch Bayes’sches Netzwerk genannt, ist ein azyklisch gerichteter Graph (DAG), wobei die Knoten Zufallsvariablen sind. Es gibt einen Bogen von jedem Element vonEltern(Xi) in Xi.Mit dem Glaubensnetzwerk ist ein Satz von bedingten Wahrscheinlichkeitsverteilungen verbunden – die bedingte Wahrscheinlichkeit jeder Variablen angesichts ihrer Eltern (was die vorherigen Wahrscheinlichkeiten der Variablen ohne Eltern einschließt).
Ein Glaubensnetz besteht also aus
- einem DAG, in dem jeder Knoten durch eine Zufallsvariable gekennzeichnet ist;
- einem Bereich für jede Zufallsvariable; und
- einem Satz von bedingten Wahrscheinlichkeitsverteilungen, die P(X|Eltern(X)) für jede Variable X angeben.
Ein Glaubensnetz ist konstruktionsbedingt azyklisch. Die Art und Weise, wie die Kettenregel die Konjunktion zerlegt, gibt die Reihenfolge vor. Unterschiedliche Zerlegungen können zu unterschiedlichen Glaubensnetzen führen.
Angenommen, wir verwenden die folgenden Variablen, die alle boolesch sind, in der folgenden Reihenfolge:
- Manipulation ist wahr, wenn es eine Manipulation des Alarms gibt.
- Feuer ist wahr, wenn es ein Feuer gibt.
- Alarm ist wahr, wenn der Alarm ertönt.
- Rauch ist wahr, wenn es Rauch gibt.
- Verlassen ist wahr, wenn es viele Personen gibt, die das Gebäude auf einmal verlassen.
- Bericht ist wahr, wenn es einen Bericht von Personen gibt, die das Gebäude verlassen. Bericht ist falsch, wenn kein Bericht über das Verlassen vorliegt.
Die Variable Bericht bezeichnet die Sensormeldung, dass Personen das Gebäude verlassen. Diese Information ist unzuverlässig, da die Person, die eine solche Meldung abgibt, einen Scherz machen könnte oder niemand, der eine solche Meldung hätte abgeben können, aufgepasst haben könnte. Diese Variable wird eingeführt, um die Konditionierung auf unzuverlässige Sensordaten zu ermöglichen. Der Agent weiß, was der Sensor meldet, hat aber nur unzuverlässige Informationen über Personen, die das Gebäude verlassen.
- Feuer ist bedingt unabhängig von Manipulation (wenn keine anderen Informationen vorliegen).
- Alarm hängt sowohl von Feuer als auch von Manipulation ab. Das heißt, wir machen keine Unabhängigkeitsannahmen darüber, wie der Alarm bei dieser Variablenanordnung von seinen Vorgängern abhängt.
- Der Rauch hängt nur vom Feuer ab und ist bedingt unabhängig von Manipulationen und dem Alarm, wenn es ein Feuer gibt.
- Das Verlassen hängt nur vom Alarm ab und nicht direkt vom Feuer oder von Manipulationen oder Rauch. Das heißt, das Verlassen ist bedingt unabhängig von den anderen Variablen, wenn Alarm gegeben ist.
- Der Bericht hängt nur direkt vom Verlassen ab.
Das Glaubensnetzwerk von Abbildung 6.1 drückt diese Abhängigkeiten aus.
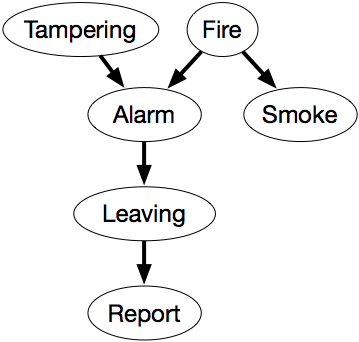
Dieses Netzwerk stellt die Faktorisierung
P(Manipulation,Feuer,Alarm,Rauch,Verlassen,Bericht) = P(Manipulation) ×P(Feuer) ×P(Alarm|Manipulation,Feuer) ×P(Rauch|Feuer) ×P(Verlassen|Alarm) ×P(Bericht|Verlassen).
Wir müssen auch den Bereich jeder Variablen definieren. Nehmen wir an, dass die Variablen boolesch sind; das heißt, sie haben den Bereich {true,false}. Wir verwenden die klein geschriebene Variante der Variablen, um den wahren Wert darzustellen, und verwenden die Negation für den falschen Wert. So wird zum Beispiel Manipulation=wahr als Manipulation geschrieben und Manipulation=falsch als ¬Manipulation geschrieben.
Die folgenden Beispiele gehen von den folgenden bedingten Wahrscheinlichkeiten aus:
P(Feuer) = 0,01
P(Alarm | Feuer ∧Manipulation) = 0.5
P(Alarm | Feuer ∧¬Verfälschung) = 0,99
P(Alarm | Feuer ∧Verfälschung) = 0,85
P(Alarm | Feuer ∧¬Verfälschung) = 0,0001
P(Rauch | Feuer ) = 0.9
P(Rauch | ¬Feuer ) = 0.01
P(Verlassen | Alarm) = 0.88
P(Verlassen | ¬Alarm ) = 0.001
P(Meldung | Verlassen ) = 0.75
P(Meldung | ¬Verlassen ) = 0.01
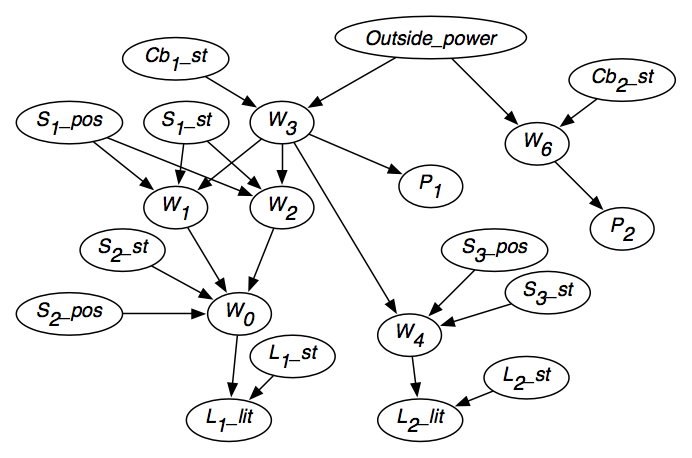
- Für jede Leitung wi gibt es eine Zufallsvariable Wi mit dem Bereich {live,dead}, die angibt, ob in der Leitung wi Strom vorhanden ist. Wi=lebendig bedeutet, dass die Leitung wi Strom hat. Wi=dead bedeutet, dass in der Leitung wi kein Strom vorhanden ist.
- Outside_power mit der Domäne {live,dead} gibt an, ob Strom in das Gebäude gelangt.
- Für jeden Schalter si bezeichnet die Variable Si_pos die Position vonsi. Sie hat den Bereich {oben,unten}.
- Für jeden Schalter si gibt die Variable Si_st den Zustand des Schalters si an. Sie hat den Bereich {ok,upside_down,short,intermittent,broken}. Si_st=ok bedeutet, dass der Schalter si normal funktioniert. Si_st=upside_down bedeutet, dass der Schalter si verkehrt herum installiert ist. Si_st=kurz bedeutet, dass der Schalter si verkürzt ist und wie ein Draht funktioniert. Si_st=broken bedeutet, dass der Schalter si kaputt ist und keinen Strom fließen lässt.
- Für jeden Stromkreisunterbrecherercbi hat die Variable Cbi_st den Bereich {on,off}. Cbi_st=on bedeutet, dass Strom durch cbi fließen kann, und Cbi_st=off bedeutet, dass kein Strom durch cbi fließen kann.
- Für jede Leuchte li bezeichnet die Variable Li_st mit der Domäne {ok,intermittierend,unterbrochen} den Zustand der Leuchte. Li_st=ok bedeutet, dass die Leuchte li leuchtet, wenn sie mit Strom versorgt wird, Li_st=intermittent bedeutet, dass die Leuchte li intermittierend leuchtet, wenn sie mit Strom versorgt wird, und Li_st=broken bedeutet, dass die Leuchte li nicht funktioniert.
Wählen wir eine Reihenfolge, bei der die Ursachen einer Variablen in der Reihenfolge vor der Variablen stehen. Zum Beispiel kommt die Variable dafür, ob ein Licht leuchtet, nach den Variablen dafür, ob das Licht funktioniert und ob Strom in das Licht fließt.
Ob die Leuchte l1 leuchtet, hängt nur davon ab, ob in der Leitung w0 Strom fließt und ob die Leuchte l1 richtig funktioniert. Andere Variablen, wie die Stellung des Schalters s1, ob das Licht l2 leuchtet oder wer die Königin von Kanada ist, sind irrelevant. Die Eltern von L1_lit sind also W0 und L1_st.
Betrachten wir die Variable W0, die angibt, ob Strom in der Leitung w0 vorhanden ist. Wenn wir wüssten, ob in den Drähten w1 und w2 Strom fließt, und wir wüssten, in welcher Position sich der Schalter s2 befindet und ob der Schalter ordnungsgemäß funktioniert, würde der Wert der anderen Variablen (außer L1_lit) keinen Einfluss darauf haben, ob im Draht w0 Strom fließt. Daher sollten die Eltern von W0 S2_Pos, S2_st, W1 und W2 sein.
Abbildung 6.2 zeigt das sich ergebende Überzeugungsnetzwerk, nachdem die Unabhängigkeit jeder Variablen berücksichtigt wurde.
Das Überzeugungsnetzwerk enthält auch die Domänen der Variablen, wie in der Abbildung angegeben, und die bedingten Wahrscheinlichkeiten für jede Variable bei ihren Eltern.
Für die Variable W1 müssen die folgenden bedingten Wahrscheinlichkeiten angegeben werden:
P(W1=lebend|S1_pos=oben ∧S1_st=ok ∧W3=lebend)
P(W1=lebend|S1_pos=oben ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=lebendig|S1_pos=unten ∧S1_st=gebrochen ∧W3=tot).
Es gibt zwei Werte für S1_pos, fünf Werte für S1_ok und zwei Werte für W3, es gibt also 2×5 ×2 = 20 verschiedene Fälle, in denen ein Wert für W1=lebendig angegeben werden muss. Aus Sicht der Wahrscheinlichkeitstheorie könnte die Wahrscheinlichkeit für W1=lebendig in diesen 20 Fällen willkürlich zugewiesen werden. Natürlich schränkt die Kenntnis des Bereichs die sinnvollen Werte ein. Die Werte für W1=Tot können aus den Werten für W1=Leben für jeden dieser Fälle berechnet werden.
Da die Variable S1_st keine Eltern hat, benötigt sie eine Vorverteilung, die als die Wahrscheinlichkeiten für alle Werte bis auf einen angegeben werden kann; der verbleibende Wert kann aus der Bedingung abgeleitet werden, dass alle Wahrscheinlichkeiten 1 ergeben. Um die Verteilung von S1_st zu spezifizieren, müssen also vier der folgenden fünf Wahrscheinlichkeiten angegeben werden:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Ein Glaubensnetz ist eine grafische Darstellung der bedingten Unabhängigkeit, die es uns erlaubt, direkte Effekte innerhalb des Graphen darzustellen und vorschreibt, welche Wahrscheinlichkeiten angegeben werden müssen. Aus dem Netzwerk können beliebige Vorhersagewahrscheinlichkeiten abgeleitet werden.
Die in ein Glaubensnetzwerk eingebettete Unabhängigkeitsannahme lautet wie folgt:Jede Zufallsvariable ist bedingt unabhängig von ihren Nicht-Nachkommen, da sie von ihren Eltern abstammt. Das heißt, wenn X eine Zufallsvariable mit Eltern Y1,…, Yn ist, sind alle Zufallsvariablen, die nicht Nachkommen vonX sind, bedingt unabhängig von X bei Y1,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
wenn R keinen Nachkommen von X einschließt. Die rechte Seite dieser Gleichung ist die Form der Wahrscheinlichkeiten, die als Teil des Glaubensnetzes spezifiziert werden.R kann Vorfahren von X und andere Knoten einbeziehen, solange sie nicht Nachkommen von X sind. Die Unabhängigkeitsannahme besagt, dass der gesamte Einfluss von Nicht-Nachkommen-Variablen durch die Kenntnis des Wertes der Eltern von X erfasst wird.
Oft wird nur die beschriftete DAG als Glaubensnetz bezeichnet. In diesem Fall ist es wichtig, sich daran zu erinnern, dass eine Domäne für jede Variable und ein Satz von bedingten Wahrscheinlichkeitsverteilungen ebenfalls Teil des Netzwerks sind.
Die Anzahl der Wahrscheinlichkeiten, die für jede Variable angegeben werden müssen, ist exponentiell zur Anzahl der Eltern der Variablen.
Die Annahme der Unabhängigkeit ist insofern nützlich, als die Anzahl der Variablen, die eine andere Variable direkt beeinflussen, gering ist. Sie sollten die Variablen so anordnen, dass die Knoten so wenig Eltern wie möglich haben.
Glaubensnetze und Kausalität
Glaubensnetze werden oft als Kausalnetze bezeichnet, und es wird behauptet, dass sie eine gute Darstellung der Kausalität sind.Erinnern Sie sich daran, dass ein Kausalmodell das Ergebnis von Interventionen vorhersagt.Nehmen wir an, Sie haben ein Kausalmodell eines Bereichs im Kopf, in dem der Bereich durch eine Menge von Zufallsvariablen spezifiziert ist. Wenn für jedes Paar von Zufallsvariablen X1 und X2 ein direkter kausaler Zusammenhang von X1 zu X2 besteht (d. h. ein Eingriff zur Veränderung von X1 in einem Kontext anderer Variablen wirkt sich auf X2 aus, und dies kann nicht durch eine intervenierende Variable modelliert werden), fügen Sie einen Bogen vonX1 zu X2 hinzu. Sie würden erwarten, dass das Kausalmodell der Unabhängigkeitsannahme des Glaubensnetzes gehorcht. Somit wären alle Schlussfolgerungen des Glaubensnetzes gültig.
Man würde auch erwarten, dass ein solcher Graph azyklisch ist; man will nicht, dass sich etwas irgendwann selbst verursacht. Diese Annahme ist vernünftig, wenn man bedenkt, dass die Zufallsvariablen bestimmte Ereignisse und nicht Ereignistypen repräsentieren. Betrachten wir beispielsweise eine Kausalkette, bei der “gestresst sein” dazu führt, dass Sie “ineffizient arbeiten”, was wiederum dazu führt, dass Sie “gestresst sind”. Um den offensichtlichen Kreislauf zu durchbrechen, können wir “gestresst sein” in verschiedenen Stadien als verschiedene Zufallsvariablen darstellen, die sich auf verschiedene Zeiten beziehen. In der Vergangenheit gestresst zu sein, führt dazu, dass Sie im Moment nicht gut arbeiten, was dazu führt, dass Sie in der Zukunft gestresst sind. Die Variablen sollten dem Grundsatz der Klarheit genügen und eine klar definierte Bedeutung haben. Die Variablen sollten nicht als Ereignistypen angesehen werden.
Das Glaubensnetz selbst hat nichts über Kausalität zu sagen und kann nicht-kausale Unabhängigkeit darstellen, aber es scheint besonders geeignet zu sein, wenn in einem Bereich Kausalität besteht. Wenn man Bögen hinzufügt, die die lokale Kausalität darstellen, ergibt sich in der Regel ein kleines Glaubensnetz. Das Glaubensnetzwerk in Abbildung 6.2 zeigt, wie dies für einen einfachen Bereich geschehen kann.
Akausale Netzwerkmodelle sind Interventionen. Würde jemand eine Variable künstlich dazu zwingen, einen bestimmten Wert anzunehmen, wären die Nachkommen der Variable – aber keine anderen Knoten – davon betroffen. Schließlich können Sie sehen, wie die Kausalität in Glaubensnetzen mit den in Abschnitt 5.7 erörterten kausalen und beweiskräftigen Schlussfolgerungen zusammenhängt. Ein kausales Glaubensnetz kann als Weg der Axiomatisierung in eine kausale Richtung betrachtet werden. Das Schließen in Glaubensnetzen entspricht dem Ableiten auf Ursachen und dem anschließenden Vorhersagen von diesen. Zwischen der in Abschnitt 5.7 erörterten logikbasierten abduktiven Sichtweise und Glaubensnetzen besteht eine direkte Zuordnung: Glaubensnetze können als logische Programme mit Wahrscheinlichkeiten über mögliche Hypothesen modelliert werden. Dies wird in Abschnitt 14.3 beschrieben.
Bei der Definition der in einem Glaubensnetz kodierten Unabhängigkeit ist die Einschränkung “jede Zufallsvariable ist bedingt unabhängig von ihren Nicht-Nachkommen, da sie ihre Eltern hat” zu beachten. WennR einen Nachkommen der Variablen X enthält, ist die Unabhängigkeitsannahme nicht direkt anwendbar.
Die Variable S1_pos hat keine Eltern. Die in das Glaubensnetz eingebettete Unabhängigkeit besagt also, dass P(S1_pos=up|A) =P(S1_pos=up) für jedes A, das keinen Nachkommen vonS1_pos einschließt. Wenn A einen Abkömmling von S1_pos=up enthält – zum Beispiel, wenn A S2_pos=up∧L1_lit=true ist – kann die Unabhängigkeitsannahme nicht direkt angewendet werden.
Dieses Netzwerk kann auf verschiedene Weise verwendet werden:
- Durch die Konditionierung auf das Wissen, dass die Schalter und Leistungsschalter in Ordnung sind, und auf die Werte der externen Leistung und die Position der Schalter kann dieses Netzwerk simulieren, wie die Beleuchtung funktionieren sollte.
- Aus den Werten der externen Stromversorgung und der Position der Schalter kann das Netzwerk die Wahrscheinlichkeit eines jeden Ergebnisses ableiten – zum Beispiel, wie wahrscheinlich es ist, dass l1 leuchtet.
- Gegebene Werte für die Schalter und die Frage, ob das Licht leuchtet, lassen auf die nachträgliche Wahrscheinlichkeit schließen, dass sich jeder Schalter oder Leistungsschalter in einem bestimmten Zustand befindet.
- Gegebene Beobachtungen können mit Hilfe des Netzwerks zurückgerechnet werden, um die wahrscheinlichste Position der Schalter zu bestimmen.
- Ausgehend von einigen Schalterpositionen, einigen Ausgängen und einigen Zwischenwerten kann das Netzwerk verwendet werden, um die Wahrscheinlichkeit jeder anderen Variablen im Netzwerk zu bestimmen.
Ein Glaubensnetzwerk spezifiziert eine gemeinsame Wahrscheinlichkeitsverteilung, aus der beliebige bedingte Wahrscheinlichkeiten abgeleitet werden können. Ein Netzwerk kann abgefragt werden, indem man nach der bedingten Wahrscheinlichkeit einer beliebigen Variablen in Abhängigkeit von den Werten einer beliebigen anderen Variablen fragt. Dies geschieht in der Regel durch die Bereitstellung von Beobachtungen zu einigen Variablen und die Abfrage einer anderen Variablen.
P(Feuer) = 0,01
P(Bericht ) = 0,028
P(Rauch) = 0.0189
Betrachtet man den Bericht, so ergibt sich folgendes:
P(Feuer |Bericht)= 0,2305
P(Rauch |Bericht) = 0,215
Wie erwartet, werden die Wahrscheinlichkeiten für Manipulation und Feuer durch den Bericht erhöht. Da die Brandwahrscheinlichkeit steigt, steigt auch die Rauchwahrscheinlichkeit.
Angenommen, es wurde Rauch beobachtet:
P(Feuer|Rauch) = 0,476
P(Bericht |Rauch) = 0,320
Beachten Sie, dass die Manipulationswahrscheinlichkeit durch die Beobachtung von Rauch nicht beeinflusst wird; die Wahrscheinlichkeiten von Bericht und Feuer werden jedoch erhöht.
Angenommen, sowohl die Meldung als auch der Rauch wurden beobachtet:
P(Feuer |Meldung ∧Rauch) = 0,964
Die Beobachtung von beidem macht Feuer noch wahrscheinlicher. Im Kontext der Meldung macht das Vorhandensein von Rauch jedoch eine Manipulation unwahrscheinlicher. Dies liegt daran, dass die Meldung durch das Feuer erklärt wird, das nun wahrscheinlicher ist.
Angenommen, die Meldung, aber nicht der Rauch, wurde beobachtet:
P(Feuer|Bericht ∧¬Rauch) = 0,0294
Im Zusammenhang mit dem Bericht wird Feuer sehr viel unwahrscheinlicher und die Wahrscheinlichkeit von Manipulationen steigt, um den Bericht zu erklären.
Dieses Beispiel veranschaulicht, wie die Unabhängigkeitsannahme eines Glaubensnetzes zu vernünftigen Schlussfolgerungen führt, und zeigt auch, wie das Wegerklären eine Folge der Unabhängigkeitsannahme eines Glaubensnetzes ist.
- 6.3.1 Konstruktion von Glaubensnetzen