Kolmogorov-Smirnov-Test
Der K-S-Test ist ein Anpassungsgütetest, der zur Beurteilung der Gleichmäßigkeit einer Reihe von Datenverteilungen verwendet wird. Er wurde als Reaktion auf die Unzulänglichkeiten des Chi-Quadrat-Tests entwickelt, der nur für diskrete, gebündelte Verteilungen präzise Ergebnisse liefert. Der K-S-Test hat den Vorteil, dass er keine Annahmen über die Einteilung der zu vergleichenden Datensätze macht, wodurch die Willkür und der Informationsverlust, die mit dem Prozess der Einteilungsauswahl einhergehen, beseitigt werden.
In der Statistik ist der K-S-Test der anerkannte Test zur Messung von Unterschieden zwischen kontinuierlichen Datensätzen (nicht gebündelte Datenverteilungen), die eine Funktion einer einzigen Variablen sind. Dieses Differenzmaß, die K-S \(D\)-Statistik, ist definiert als der Maximalwert der absoluten Differenz zwischen zwei kumulativen Verteilungsfunktionen. Der einseitige K-S-Test wird verwendet, um einen Datensatz mit einer bekannten kumulativen Verteilungsfunktion zu vergleichen, während der zweiseitige K-S-Test zwei verschiedene Datensätze vergleicht. Jeder Datensatz ergibt eine andere kumulative Verteilungsfunktion, deren Bedeutung in ihrer Beziehung zu der Wahrscheinlichkeitsverteilung liegt, aus der der Datensatz gezogen wird: Die Wahrscheinlichkeitsverteilungsfunktion für eine einzelne unabhängige Variable \(x\) ist eine Funktion, die jedem Wert von \(x\) eine Wahrscheinlichkeit zuweist. Die Wahrscheinlichkeit, die für einen bestimmten Wert \(x_{i}\) angenommen wird, ist der Wert der Wahrscheinlichkeitsverteilungsfunktion bei \(x_{i}\) und wird mit \(P(x_{i})\) bezeichnet.Die kumulative Verteilungsfunktion ist definiert als die Funktion, die den Anteil der Datenpunkte links von einem bestimmten Wert \(x_{i}\) angibt, \(P(x <x_{i})\); sie stellt die Wahrscheinlichkeit dar, dass \(x\) kleiner oder gleich einem bestimmten Wert \(x_{i}\) ist.
Für den Vergleich zweier unterschiedlicher kumulativer Verteilungsfunktionen \(S_{N1}(x)\) und \(S_{N2}(x)\) lautet die K-S-Statistik also
D = max|S_N1(x) – S_N2(x)|
wobei \(S_{N}(x)\) die kumulative Verteilungsfunktion der Wahrscheinlichkeitsverteilung ist, aus der ein Datensatz mit \(N\) Ereignissen gezogen wird. Wenn sich \(N\) geordnete Ereignisse an Datenpunkten \(x_{i}\) befinden, wobei \(i = 1, \ldots, N\), dann
S_N(x_i) = (i-N)/N
, wobei die \(x\)-Datenreihe in aufsteigender Reihenfolge sortiert ist. Dies ist eine Schrittfunktion, die um \(1/N\) beim Wert jedes geordneten Datenpunktes zunimmt.
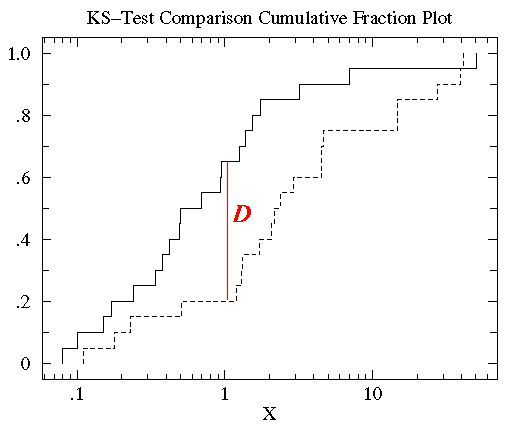
Kirkman, T.W. (1996) Statistists to Use.
http://www.physics.csbsju.edu/stats/
Für unsere Zwecke werden die beiden Verteilungen verglichen, nämlich die gemessene Verteilung der Ankunftszeiten und der akkumulierte Anteil am verstrichenen Zeitintervall. Wenn die Nullhypothese (keine Variabilität) zutrifft, erhalten wir 50 % der Ereignisse in 50 % der verstrichenen Zeit, und die \(D\)-Statistik sollte sich gemäß der Kolmogorov-Verteilung für viele Realisierungen der Ankunftszeitverteilung verteilen. Die vom Test gelieferte Wahrscheinlichkeit ist also \(p_{KS} = 1 – \alpha\), wobei \(\alpha\) die Wahrscheinlichkeit (gemäß der Kolmogorov-Verteilung) ist, dass der Wert von \(D\) größer oder gleich dem gemessenen Wert ist. Ein kleiner Wert von \(p_{KS}\) zeigt daher die Übereinstimmung mit der Nullhypothese an, während ein großer Wert von \(p_{KS}\) anzeigt, dass das Intervall zwischen den Ereignissen nicht konstant ist und daher auf Variabilität geschlossen werden kann.