von Evan Ma

(Mathe- und Physiklehrer im The Edge Learning Center)

Die logarithmische Funktion scheint viele Schüler zu verwirren, die das IB Math SL Programm studieren. Um sie richtig zu verstehen, definieren wir

wobei , eine streng positive reelle Zahl, als Basis bezeichnet wird und die Potenz ist. Wir alle kennen zum Beispiel die folgenden Zahlen auswendig:

und so weiter. Die logarithmische Funktion macht es umgekehrt – mit einer Zahl als Argument ergibt sie die Potenz in Abhängigkeit von einer bestimmten Basis und ist daher wie folgt definiert.

Wenn

dann

Daher ist es klar, dass

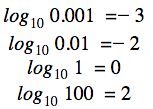
und so weiter. Betrachten wir weitere Beispiele mit anderen Basen:

Lösen wir zur Übung die folgenden Fragen: (a) , (b) , (c) , (d) . Die Antworten finden Sie am Ende dieses Blogs.

Aus der Definition des Logarithmus können wir auch ersehen, dass wir, wenn wir die Basis um den Basis-logarithmus einer reellen Zahl erhöhen, die Zahl zurückbekommen, nämlich

Sie können versuchen, dies mit Ihrem Taschenrechner für verschiedene gültige Basen zu überprüfen. Diese Identität ist wichtig, wenn wir versuchen, logarithmische Gleichungen zu lösen, wofür wir Beispiele geben werden.

Lassen Sie uns nun einen Blick auf die Regeln des Logarithmus werfen. Ähnlich wie bei der Definition des Logarithmus verwenden wir die Gesetze der Indizes, um die Regeln abzuleiten:

1. Logarithmus eines Produktes ist Summe der Logarithmen

Beweis: Sagen wir und , also

2. Basis- Logarithmus von Mr ist mal

Beweis: Sage , also

3. Der Logarithmus eines Quotienten ist die Differenz der Logarithmen

Beweis: Sagen wir und , also

4. Die letzte Regel nennt man die Basiswechselformel. Wir verwenden ein Beispiel, um die Formel abzuleiten. Nehmen wir an, wir wollen wissen, welche Potenz von 2 erhöht werden muss, um 50 zu erhalten. Da 50 keine ganzzahlige Potenz von 2 ist, ist die Antwort nicht sehr offensichtlich. Wir schreiben also

und damit. Um zu finden, wenden wir den Logarithmus zur Basis 10 auf beide Seiten der Gleichung an, da unser Taschenrechner möglicherweise nicht über die Logarithmentaste zur Basis 2 verfügt:

Auf 4 signifikante Stellen korrigiert, beträgt der Wert von ungefähr 5,644. Du kannst deine Antwort überprüfen, indem du 2 hoch 5,644 erhöhst, um zu sehen, dass die Antwort ungefähr 50 ist.

Um das Problem zu verallgemeinern, nehmen wir an, wir müssen so finden, dass und der Logarithmus zur Basis- nicht zur Verfügung steht, können wir stattdessen den Logarithmus zur Basis gemäß der Gleichung

verwenden und daher

Betrachten wir als Beispiel folgendes. Angenommen, ein Betrag von 10.000 $ wird zu einem Zinssatz von 2,5 % pro Jahr mit jährlicher Zinseszinsung eingezahlt. Wie lange muss das Geld auf dem Konto verbleiben, damit es auf 50.000 $ anwächst?

Um die Frage zu beantworten, versuchen wir im Grunde, n so zu finden, dass

Da mein einfacher wissenschaftlicher Taschenrechner mir nicht erlaubt, eine Basis von 1 anzugeben.025 für den logarithmischen Schlüssel anzugeben, muss ich mich auf die Formel für den Basenwechsel verlassen und die Basis 10 verwenden, also

Da die Zinsen jährlich aufgezinst werden, dauert es 66 Jahre, bis sie mindestens 5-mal gewachsen sind.

Nachdem wir die Regeln des Logarithmus erforscht haben, führen wir die natürliche logarithmische Funktion oder ein. Sie ist Basis-, wobei die bedeutende irrationale Zahl ≈2,71828 ist, deren Bedeutung in den Naturwissenschaften und der Mathematik nicht genug betont werden kann. Der Basis-Logarithmus ist also wie folgt definiert.

Wenn

dann

Nun wollen wir uns zwei Beispiele ansehen, bei denen häufig Fehler beim Lösen von Logarithmusgleichungen gemacht werden. Versuchen Sie, den Fehler zu erkennen.

Wo liegt der Fehler? Schau genauer hin. Natürlich kann man im zweiten Schritt den Logarithmus nicht durch das Additionszeichen “teilen”. Denken Sie daran, dass Sie einen Logarithmus nur dann in eine Summe “aufspalten” können, wenn der Logarithmus auf ein Produkt und nicht auf eine Summe angewendet wird. Die korrekten Schritte lauten also wie folgt:

Schauen wir uns nun das folgende Beispiel an und sehen wir, ob Sie den Fehler erkennen können:

Wo liegt der Fehler? Ja, er liegt im zweiten Schritt – ein Quotient von Logarithmen ist natürlich nicht der Logarithmus des Quotienten. Vielmehr können wir die Formel für den Basenwechsel verwenden, um den ersten Schritt wie folgt zu vereinfachen:

Schließlich wollen wir veranschaulichen, wie man die Regeln des Logarithmus verwendet, um die folgende Aufgabe zu lösen:

Sie werden feststellen, dass die Unbekannte als Basis und als Variable im Argument des Logarithmus erscheint. Wie können wir lösen? Die Methode hängt immer noch von der konsequenten Anwendung der Regeln des Logarithmus ab. Zunächst erheben wir beide Seiten als Potenzen der Basis , und somit

Du erinnerst dich vielleicht an die Definition des Logarithmus, dass die linke Seite einfach das Argument des Logarithmus wird, und daher

Durch Umstellen der obigen Gleichung müssen wir

Nachdem wir festgestellt haben, dass diese Gleichung einer Quadratischen in ähnelt, lösen wir wie folgt:

Nun, wo ist die negative Wurzel? Da auch die Basis des Logarithmus ist, wird die negative Wurzel als Lösung verworfen. Daher ist die endgültige Antwort.

Anhand der obigen Beispiele kannst du sehen, dass das Lösen einer scheinbar schwierigen logarithmischen Gleichung überhaupt nicht schwer ist – wende einfach die Regeln des Logarithmus konsequent an und du erhältst die richtige Lösung.

Antworten auf Fragen: (a) 2 (b) 3 (c) -3 (d) -2.