Der StatsTest Ablauf: Vorhersage >> Kontinuierliche abhängige Variable >> Mehr als eine unabhängige Variable >> Keine wiederholten Messungen >> Eine abhängige Variable

Sind Sie nicht sicher, ob dies die richtige statistische Methode ist? Verwenden Sie den Arbeitsablauf “Choose Your StatsTest”, um die richtige Methode auszuwählen.

Was ist multivariate multiple lineare Regression?

Multivariate multiple lineare Regression ist ein statistischer Test, der zur Vorhersage mehrerer Ergebnisvariablen unter Verwendung einer oder mehrerer anderer Variablen verwendet wird. Sie wird auch verwendet, um die numerische Beziehung zwischen diesen Gruppen von Variablen und anderen zu bestimmen. Die Variable, die Sie vorhersagen wollen, sollte kontinuierlich sein, und Ihre Daten sollten die anderen unten aufgeführten Annahmen erfüllen.

Annahmen für die multivariate multiple lineare Regression

Jede statistische Methode hat Annahmen. Annahmen bedeuten, dass Ihre Daten bestimmte Eigenschaften erfüllen müssen, damit die Ergebnisse der statistischen Methode korrekt sind.

Die Annahmen für die multivariate lineare Mehrfachregression umfassen:

1. Linearität
2. Keine Ausreißer
3. Gleiche Streuung über den Bereich
4. Normalität der Residuen
5. Keine Multikollinearität

Lassen Sie uns auf jede dieser Eigenschaften einzeln eingehen.

Linearität

Die Variablen, die Sie interessieren, müssen in einem linearen Zusammenhang stehen. Das bedeutet, dass Sie, wenn Sie die Variablen aufzeichnen, eine gerade Linie zeichnen können, die der Form der Daten entspricht.

Keine Ausreißer

Die Variablen, die Sie interessieren, dürfen keine Ausreißer enthalten. Die lineare Regression reagiert empfindlich auf Ausreißer oder Datenpunkte, die ungewöhnlich große oder kleine Werte aufweisen. Sie können feststellen, ob Ihre Variablen Ausreißer enthalten, indem Sie sie aufzeichnen und beobachten, ob einige Punkte weit von allen anderen Punkten entfernt sind.

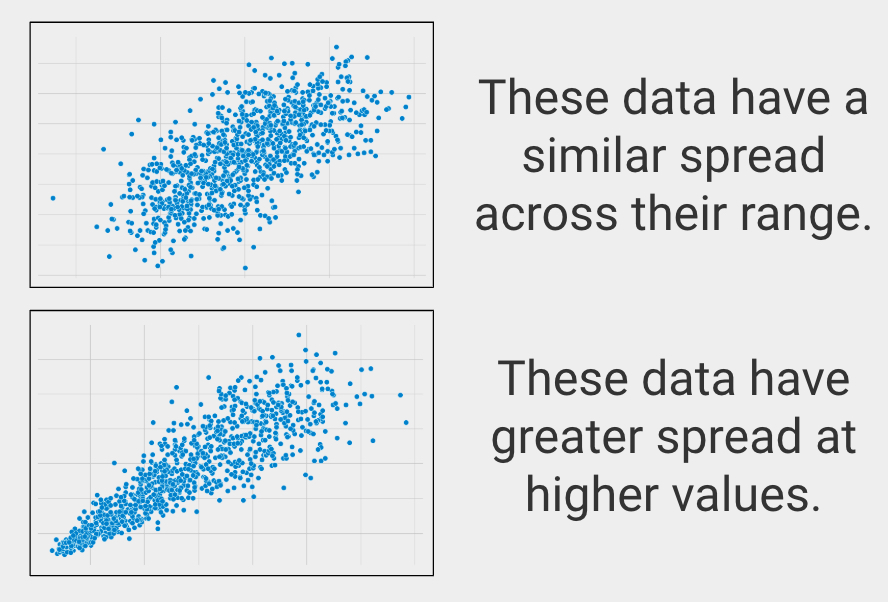
Gleiche Streuung über den Bereich

In der Statistik wird dies Homoskedastizität genannt, die beschreibt, wenn Variablen eine ähnliche Streuung über ihre Bereiche haben.

Normalität der Residuen

Das Wort “Residuen” bezieht sich auf die Werte, die sich aus der Subtraktion der erwarteten (oder vorhergesagten) abhängigen Variablen von den tatsächlichen Werten ergeben. Die Verteilung dieser Werte sollte der Form einer Normalverteilung (oder Glockenkurve) entsprechen.

Die Erfüllung dieser Annahme gewährleistet, dass die Ergebnisse der Regression über die gesamte Bandbreite der Daten gleichmäßig anwendbar sind und dass es keine systematische Verzerrung bei der Vorhersage gibt.

Keine Multikollinearität

Multikollinearität bezieht sich auf das Szenario, wenn zwei oder mehr der unabhängigen Variablen untereinander erheblich korreliert sind. Wenn Multikollinearität vorliegt, werden die Regressionskoeffizienten und die statistische Signifikanz instabil und weniger vertrauenswürdig, obwohl sie keinen Einfluss darauf haben, wie gut das Modell an sich zu den Daten passt.

Wann ist die multivariate multiple lineare Regression zu verwenden?

Die multivariate multiple lineare Regression sollte in den folgenden Szenarien verwendet werden:

1. Sie möchten eine Variable für die Vorhersage mehrerer anderer Variablen verwenden, oder Sie möchten die numerische Beziehung zwischen ihnen quantifizieren
2. Die Variablen, die Sie vorhersagen möchten (Ihre abhängige Variable), sind kontinuierlich
3. Sie haben mehr als eine unabhängige Variable, oder eine Variable, die Sie als Prädiktor verwenden
4. Sie haben keine wiederholten Messungen aus derselben Beobachtungseinheit
5. Sie haben mehr als eine abhängige Variable

Lassen Sie uns diese Punkte klären, damit Sie wissen, wann Sie die multivariate multiple lineare Regression verwenden sollten.

Vorhersage

Sie suchen nach einem statistischen Test, um eine Variable anhand einer anderen vorherzusagen. Dies ist eine Vorhersagefrage. Andere Arten von Analysen umfassen die Untersuchung der Stärke der Beziehung zwischen zwei Variablen (Korrelation) oder die Untersuchung von Unterschieden zwischen Gruppen (Differenz).

Kontinuierliche abhängige Variable

Die Variable, die Sie vorhersagen möchten, muss kontinuierlich sein. Kontinuierlich bedeutet, dass die Variable, die Sie vorhersagen wollen, im Grunde jeden beliebigen Wert annehmen kann, z. B. Herzfrequenz, Größe, Gewicht, Anzahl der Eisriegel, die Sie in einer Minute essen können, usw.

Zu den Datentypen, die NICHT kontinuierlich sind, gehören geordnete Daten (z. B. die Platzierung in einem Rennen, die besten Unternehmensrankings usw.), kategorische Daten (Geschlecht, Augenfarbe, Rasse usw.) oder binäre Daten (das Produkt gekauft oder nicht, die Krankheit hat oder nicht usw.).

Wenn Ihre abhängige Variable binär ist, sollten Sie die multiple logistische Regression verwenden, und wenn Ihre abhängige Variable kategorisch ist, sollten Sie die multinomiale logistische Regression oder die lineare Diskriminanzanalyse verwenden.

Mehr als eine unabhängige Variable

Die multivariate multiple lineare Regression wird verwendet, wenn es eine oder mehrere Prädiktorvariablen mit mehreren Werten für jede Beobachtungseinheit gibt.

Keine wiederholten Maßnahmen

Diese Methode eignet sich für das Szenario, wenn es nur eine Beobachtung für jede Beobachtungseinheit gibt. Die Beobachtungseinheit ist das, was einen “Datenpunkt” ausmacht, z. B. ein Geschäft, ein Kunde, eine Stadt usw.

Wenn Sie eine oder mehrere unabhängige Variablen haben, die aber für dieselbe Gruppe zu mehreren Zeitpunkten gemessen werden, dann sollten Sie ein Modell mit gemischten Effekten verwenden.

Mehr als eine abhängige Variable

Um eine multivariate multiple lineare Regression durchzuführen, sollten Sie mehr als eine abhängige Variable haben oder eine Variable, die Sie vorherzusagen versuchen.

Wenn Sie nur eine Variable vorhersagen, sollten Sie eine multiple lineare Regression verwenden.

Multivariate multiple lineare Regression Beispiel

Abhängige Variable 1: Einnahmen
Abhängige Variable 2: Kundenverkehr
Abhängige Variable 1: Werbeausgaben nach Stadt
Abhängige Variable 2: Einwohnerzahl der Stadt

Die Nullhypothese, d.h. die statistische Fachsprache für den Fall, dass die Behandlung nichts bewirkt, besagt, dass es keine Beziehung zwischen den Werbeausgaben und den Werbeausgaben oder der Einwohnerzahl nach Stadt gibt. Mit unserem Test wird die Wahrscheinlichkeit bewertet, dass diese Hypothese zutrifft.

Wir sammeln unsere Daten und führen die Analyse durch, nachdem wir sichergestellt haben, dass die Annahmen der linearen Regression erfüllt sind.

Diese Analyse führt im Grunde zweimal eine multiple lineare Regression mit beiden abhängigen Variablen durch. Wenn wir also diese Analyse durchführen, erhalten wir Beta-Koeffizienten und p-Werte für jeden Term im Modell “Umsatz” und im Modell “Kundenverkehr”. Für jedes lineare Regressionsmodell gibt es einen Betakoeffizienten, der dem Achsenabschnitt der linearen Regressionslinie entspricht (oft mit einer 0 als β0 bezeichnet). Dies ist einfach der Punkt, an dem die Regressionslinie die y-Achse kreuzt, wenn Sie Ihre Daten aufzeichnen würden. Im Falle einer multiplen linearen Regression gibt es zusätzlich noch zwei weitere Betakoeffizienten (β1, β2 usw.), die die Beziehung zwischen den unabhängigen und abhängigen Variablen darstellen.

Diese zusätzlichen Betakoeffizienten sind der Schlüssel zum Verständnis der numerischen Beziehung zwischen Ihren Variablen. Im Wesentlichen wird erwartet, dass sich Ihre abhängige Variable für jede Einheit (Wert 1), um die eine bestimmte unabhängige Variable zunimmt, um den Wert des Beta-Koeffizienten ändert, der mit dieser unabhängigen Variable verbunden ist (während andere unabhängige Variablen konstant gehalten werden).

Der p-Wert, der mit diesen zusätzlichen Beta-Werten verbunden ist, ist die Wahrscheinlichkeit, dass unsere Ergebnisse davon ausgehen, dass es tatsächlich keine Beziehung zwischen dieser Variablen und den Einnahmen gibt. Ein p-Wert kleiner oder gleich 0,05 bedeutet, dass unser Ergebnis statistisch signifikant ist und wir darauf vertrauen können, dass der Unterschied nicht nur auf Zufall zurückzuführen ist. Um einen allgemeinen p-Wert für das Modell und einzelne p-Werte zu erhalten, die die Auswirkungen der Variablen auf die beiden Modelle darstellen, werden häufig MANOVAs verwendet.

Darüber hinaus ergibt diese Analyse einen R-Quadrat-Wert (R2). Dieser Wert kann zwischen 0 und 1 liegen und gibt an, wie gut die lineare Regressionslinie mit den Datenpunkten übereinstimmt. Je höher der R2-Wert ist, desto besser passt das Modell zu den Daten.

Häufig gestellte Fragen

Q: Was ist der Unterschied zwischen der multivariaten multiplen linearen Regression und der mehrfachen Durchführung der linearen Regression?
A: Sie sind konzeptionell ähnlich, da die einzelnen Modellkoeffizienten in beiden Szenarien gleich sind. Ein wesentlicher Unterschied besteht jedoch darin, dass Signifikanztests und Konfidenzintervalle für die multivariate lineare Regression die mehrfachen abhängigen Variablen berücksichtigen.

Q: Wie führe ich eine multivariate multiple lineare Regression in SPSS, R, SAS oder STATA durch?
A: Diese Ressource soll Ihnen helfen, jedes Mal die richtige statistische Methode zu wählen. Es gibt viele Ressourcen, die Ihnen dabei helfen, herauszufinden, wie Sie diese Methode mit Ihren Daten durchführen können:
R Artikel: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/

Hilfe!

Wenn Sie immer noch nicht weiter wissen, können Sie sich gerne an uns wenden.