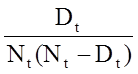Es gibt verschiedene Möglichkeiten, eine Überlebensfunktion oder eine Überlebenskurve zu schätzen. Es gibt eine Reihe beliebter parametrischer Methoden, die zur Modellierung von Überlebensdaten verwendet werden, und sie unterscheiden sich in Bezug auf die Annahmen, die über die Verteilung der Überlebenszeiten in der Population getroffen werden. Zu den gängigen Verteilungen gehören die Exponential-, Weibull-, Gompertz- und Log-Normal-Verteilung.2 Die vielleicht populärste ist die Exponentialverteilung, die davon ausgeht, dass die Wahrscheinlichkeit eines Teilnehmers, das interessierende Ereignis zu erleiden, unabhängig davon ist, wie lange diese Person ereignisfrei war. Andere Verteilungen gehen von unterschiedlichen Annahmen über die Wahrscheinlichkeit aus, dass eine Person ein Ereignis entwickelt (d. h. sie kann im Laufe der Zeit zunehmen, abnehmen oder sich verändern). Weitere Einzelheiten zu parametrischen Methoden der Überlebensanalyse finden sich in Hosmer und Lemeshow und Lee und Wang1,3.

Wir konzentrieren uns hier auf zwei nichtparametrische Methoden, die keine Annahmen darüber treffen, wie sich die Wahrscheinlichkeit, dass eine Person ein Ereignis entwickelt, im Laufe der Zeit verändert. Mit nichtparametrischen Methoden wird die Überlebensverteilung oder die Überlebenskurve geschätzt und dargestellt. Überlebenskurven werden häufig als Stufenfunktionen dargestellt, wie in der folgenden Abbildung zu sehen ist. Die Zeit wird auf der X-Achse und das Überleben (Anteil der gefährdeten Personen) auf der Y-Achse dargestellt. Beachten Sie, dass der Prozentsatz der überlebenden Teilnehmer nicht immer dem Prozentsatz der Überlebenden entspricht (was voraussetzt, dass der Tod das Ergebnis von Interesse ist). “Überleben” kann sich auch auf den Anteil beziehen, der frei von einem anderen Ergebnisereignis ist (z. B. Prozentsatz frei von Herzinfarkt oder Herz-Kreislauf-Erkrankungen), oder es kann auch den Prozentsatz darstellen, der kein gesundes Ergebnis erfährt (z. B. Krebsremission).

Überlebensfunktion

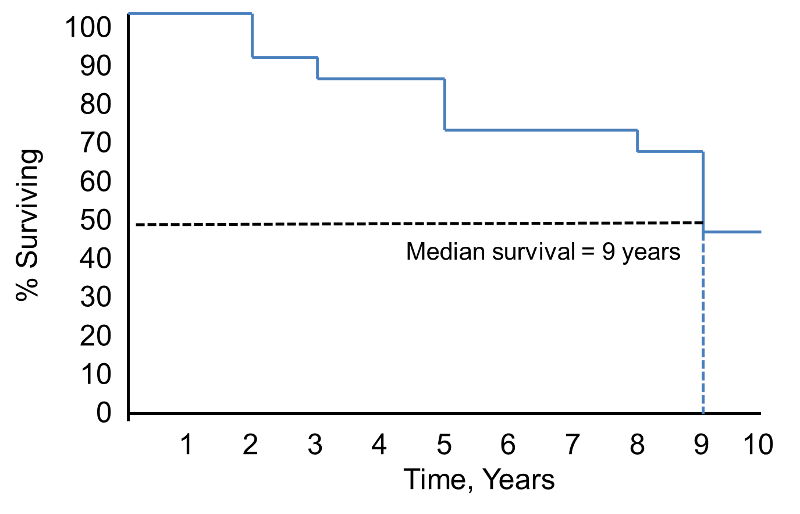
Beachten Sie, dass die Überlebenswahrscheinlichkeit 2 Jahre lang 100% beträgt und dann auf 90% sinkt. Das mediane Überleben beträgt 9 Jahre (d. h. 50 % der Bevölkerung überleben 9 Jahre; siehe gestrichelte Linien).

Beispiel:

Betrachten Sie eine kleine prospektive Kohortenstudie, die die Zeit bis zum Tod untersuchen soll. Die Studie umfasst 20 Teilnehmer, die 65 Jahre und älter sind; sie werden über einen Zeitraum von 5 Jahren aufgenommen und bis zu 24 Jahre lang verfolgt, bis sie sterben, die Studie beendet wird oder sie aus der Studie ausscheiden (lost to follow-up). Die Daten sind nachstehend aufgeführt. In der Studie gibt es 6 Todesfälle und 3 Teilnehmer mit vollständiger Nachbeobachtung (d. h. 24 Jahre). Die verbleibenden 11 Teilnehmer haben weniger als 24 Jahre Nachbeobachtungszeit, weil sie zu spät eingeschrieben wurden oder die Nachbeobachtung verloren haben.

Teilnehmeridentifikationsnummer	Jahr des Todes	Jahr des letzten Kontakts
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

Lebenstabelle (versicherungsmathematische Tabelle)

Eine Möglichkeit, die Erfahrungen der Teilnehmer zusammenzufassen, ist eine Lebenstabelle, oder einer versicherungsmathematischen Tabelle. Sterbetafeln werden in der Versicherungsbranche häufig verwendet, um die Lebenserwartung zu schätzen und die Prämien festzulegen. Wir konzentrieren uns auf eine bestimmte Art von Sterbetafel, die in der biostatistischen Analyse weit verbreitet ist: die Kohortensterbetafel oder Follow-up Sterbetafel. Die Follow-up-Lebenszeittabelle fasst die Erfahrungen der Teilnehmer einer Kohortenstudie oder einer klinischen Studie über einen vordefinierten Nachbeobachtungszeitraum zusammen, und zwar bis zum Zeitpunkt des interessierenden Ereignisses oder bis zum Ende der Studie, je nachdem, was zuerst eintritt.

Um eine Lebenszeittabelle zu erstellen, teilen wir zunächst die Nachbeobachtungszeiten in gleichmäßige Intervalle ein. In der obigen Tabelle haben wir eine maximale Nachbeobachtungszeit von 24 Jahren, und wir betrachten 5-Jahres-Intervalle (0-4, 5-9, 10-14, 15-19 und 20-24 Jahre). Wir addieren die Zahl der Teilnehmer, die zu Beginn jedes Intervalls noch leben, die Zahl derer, die sterben, und die Zahl derer, die in jedem Intervall zensiert werden.

Intervall in Jahren	Anzahl der Lebenden zu Beginn des Intervalls	Anzahl der Todesfälle während des Intervalls	Anzahl zensiert
0-4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

Wir verwenden die folgende Notation in unserer Lebenstabellenanalyse. Wir definieren zunächst die Notation und verwenden sie dann, um die Sterbetafel zu erstellen.

• Nt = Anzahl der Teilnehmer, die während des Intervalls t ereignisfrei sind und als gefährdet gelten (z.B., in diesem Beispiel die Anzahl der Lebenden, da unser interessierendes Ergebnis der Tod ist)
• Dt = Anzahl der Teilnehmer, die während des Intervalls t sterben (oder das interessierende Ereignis erleiden)
• Ct = Anzahl der Teilnehmer, die während des Intervalls t zensiert werden Nt* = die durchschnittliche Anzahl der Teilnehmer, die während des Intervalls t gefährdet sind
• Nt* = die durchschnittliche Anzahl der Teilnehmer, die während des Intervalls t gefährdet sind [Bei der Konstruktion von versicherungsmathematischen Sterbetafeln werden häufig die folgenden Annahmen getroffen: Erstens wird angenommen, dass die interessierenden Ereignisse (z. B. Todesfälle) am Ende des Intervalls eintreten, und es wird angenommen, dass die zensierten Ereignisse gleichmäßig (oder gleichmäßig) über das gesamte Intervall verteilt auftreten. Daher wird häufig eine Anpassung von Nt vorgenommen, um die durchschnittliche Anzahl der Teilnehmer mit Risiko während des Intervalls, Nt*, widerzuspiegeln, die wie folgt berechnet wird: Nt* =Nt-Ct/2 (d.h.,
• qt = Anteil, der während des Intervalls t stirbt (oder ein Ereignis erleidet), qt = Dt/Nt*
• pt = Anteil, der das Intervall t überlebt (oder ereignisfrei bleibt), pt = 1-qt
• St, der Anteil, der das Intervall t überlebt (oder ereignisfrei bleibt); dies wird manchmal als kumulative Überlebenswahrscheinlichkeit bezeichnet und wird wie folgt berechnet: Zunächst wird der Anteil der Teilnehmer, die nach dem Zeitpunkt 0 (dem Startzeitpunkt) überleben, definiert als S0 = 1 (alle Teilnehmer leben oder sind zum Zeitpunkt Null oder zu Beginn der Studie ereignisfrei). Der Anteil der Teilnehmer, die jedes nachfolgende Intervall überleben, wird anhand der Prinzipien der bedingten Wahrscheinlichkeit berechnet, die im Modul über Wahrscheinlichkeit eingeführt wurden. Konkret lautet die Wahrscheinlichkeit, dass ein Teilnehmer das Intervall 1 überlebt, S1 = p1. Die Wahrscheinlichkeit, dass ein Teilnehmer das Intervall 2 überlebt, bedeutet, dass er das Intervall 1 und das Intervall 2 überleben musste: S2 = P(überlebe das Intervall 2) = P(überlebe das Intervall 2)*P(überlebe das Intervall 1), oder S2 = p2*S1. Im Allgemeinen ist St+1 = pt+1*St.

Das Format der Tabelle für die Nachbeobachtungszeit ist unten dargestellt.

Für das erste Intervall, 0-4 Jahre: Zum Zeitpunkt 0, dem Beginn des ersten Intervalls (0-4 Jahre), gibt es 20 lebende oder gefährdete Teilnehmer. Zwei Teilnehmer sterben in dem Intervall und 1 wird zensiert. Wir wenden die Korrektur für die Anzahl der Teilnehmer an, die während dieses Intervalls zensiert werden, um Nt* =Nt-Ct/2 = 20-(1/2) = 19,5 zu erhalten. Die Berechnungen der übrigen Spalten sind in der Tabelle dargestellt. Die Wahrscheinlichkeit, dass ein Teilnehmer mehr als 4 Jahre oder mehr als das erste Intervall (unter Verwendung der oberen Grenze des Intervalls zur Definition der Zeit) überlebt, ist S4 = p4 = 0,897.

Für das zweite Intervall, 5-9 Jahre: Die Anzahl der Risikopersonen ist die Anzahl der Risikopersonen im vorherigen Intervall (0-4 Jahre) abzüglich derjenigen, die sterben und zensiert werden (d. h. Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). Die Wahrscheinlichkeit, dass ein Teilnehmer mehr als 9 Jahre überlebt, ist S9 = p9*S4 = 0,937*0,897 = 0,840.

Intervall in Jahren	Anzahl der Gefährdeten während des Intervalls, Nt	Durchschnittliche Anzahl der Gefährdeten während des Intervalls, Nt*	Anzahl der Todesfälle während des Intervalls, Dt	Lost to Follow-Up, Ct	Anteil der Sterbefälle während des Intervalls, qt	Anteil der Überlebenden unter den Risikogruppen Intervall, pt	Überlebenswahrscheinlichkeit St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

Die vollständige Nachlebenszeittabelle ist unten dargestellt.

Intervall in Jahren	Anzahl der Risikopatienten während des Intervalls, Nt	Durchschnittliche Anzahl der Risikopatienten während des Intervalls, Nt*	Anzahl der Todesfälle während des Intervalls, Dt	Lost to Follow-Up, Ct	Anteil der Sterbefälle während des Intervalls, qt	Anteil der Risikopersonen, Anteil der Überlebenden Intervall, pt	Überlebenswahrscheinlichkeit St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Diese Tabelle verwendet die versicherungsmathematische Methode, um die Nachlebenszeittabelle zu konstruieren, bei der die Zeit in gleichmäßige Intervalle unterteilt ist.

Kaplan-Meier (Product Limit)-Ansatz

Ein Problem bei dem oben dargestellten Lebenszeittabellen-Ansatz ist, dass sich die Überlebenswahrscheinlichkeiten ändern können, je nachdem wie die Intervalle organisiert sind, insbesondere bei kleinen Stichproben. Der Kaplan-Meier-Ansatz, der auch als Produkt-Limit-Ansatz bezeichnet wird, ist ein beliebter Ansatz, der dieses Problem löst, indem er die Überlebenswahrscheinlichkeit jedes Mal neu schätzt, wenn ein Ereignis eintritt.

Die angemessene Verwendung des Kaplan-Meier-Ansatzes beruht auf der Annahme, dass die Zensierung unabhängig von der Wahrscheinlichkeit ist, das interessierende Ereignis zu entwickeln, und dass die Überlebenswahrscheinlichkeiten bei Teilnehmern, die früh und später in die Studie aufgenommen werden, vergleichbar sind. Beim Vergleich mehrerer Gruppen ist es außerdem wichtig, dass diese Annahmen in jeder Vergleichsgruppe erfüllt sind und dass beispielsweise die Zensierung in einer Gruppe nicht wahrscheinlicher ist als in einer anderen.

Die nachstehende Tabelle verwendet den Kaplan-Meier-Ansatz, um dieselben Daten darzustellen, die oben unter Verwendung des Lebenszeittabellenansatzes präsentiert wurden. Beachten Sie, dass wir die Tabelle mit Zeit=0 und Überlebenswahrscheinlichkeit = 1 beginnen. Zum Zeitpunkt=0 (Baseline oder Beginn der Studie) sind alle Teilnehmer gefährdet und die Überlebenswahrscheinlichkeit ist 1 (oder 100%). Mit dem Kaplan-Meier-Ansatz wird die Überlebenswahrscheinlichkeit mit St+1 = St*((Nt+1-Dt+1)/Nt+1) berechnet. Beachten Sie, dass die Berechnungen nach dem Kaplan-Meier-Ansatz denen nach dem versicherungsmathematischen Sterbetafelansatz ähneln. Der Hauptunterschied besteht in den Zeitintervallen, d. h. beim versicherungsmathematischen Ansatz der Sterbetafel werden gleichmäßig verteilte Intervalle betrachtet, während beim Kaplan-Meier-Ansatz beobachtete Ereigniszeiten und Zensierungszeiten verwendet werden. Die Berechnungen der Überlebenswahrscheinlichkeiten werden in den ersten Zeilen der Tabelle detailliert dargestellt.

Lebenszeittabelle unter Verwendung des Kaplan-Meier-Ansatzes

Zeit, Jahre	Anzahl der Risikopatienten Nt	Anzahl der Todesfälle Dt	Anzahl zensiert Ct	Überlebenswahrscheinlichkeit St+1 = St*((Nt+1-Dt+1)/Nt+1)
0	20			1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3		3	0.507

Bei großen Datensätzen sind diese Berechnungen mühsam. Diese Analysen können jedoch mit statistischen Berechnungsprogrammen wie SAS erstellt werden. Excel kann auch zur Berechnung der Überlebenswahrscheinlichkeiten verwendet werden, wenn die Daten nach Zeiten geordnet sind und die Anzahl der Ereignisse und zensierten Zeiten zusammengefasst sind.

Aus der Lebenszeittabelle können wir eine Kaplan-Meier-Überlebenskurve erstellen.

Kaplan-Meier-Überlebenskurve für die obigen Daten

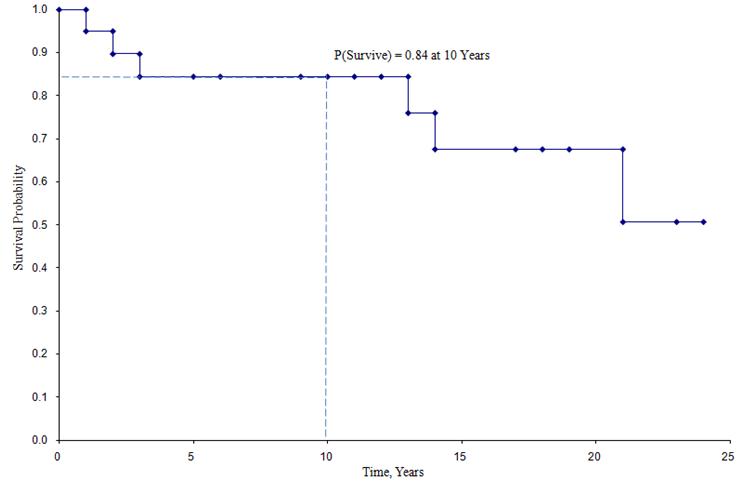
In der oben gezeigten Überlebenskurve stellen die Symbole jeden Ereigniszeitpunkt dar, entweder einen Todesfall oder einen zensierten Zeitpunkt. Aus der Überlebenskurve lässt sich auch die Wahrscheinlichkeit abschätzen, dass ein Teilnehmer mehr als 10 Jahre überlebt, indem man 10 Jahre auf der X-Achse ansetzt und auf der Y-Achse nach oben und nach unten liest. Der Anteil der Teilnehmer, die mehr als 10 Jahre überleben, beträgt 84 %, und der Anteil der Teilnehmer, die mehr als 20 Jahre überleben, beträgt 68 %. Die mittlere Überlebensdauer wird geschätzt, indem man auf der Y-Achse den Wert 0,5 ansetzt und auf der X-Achse nach oben und unten abliest. Die mediane Überlebenszeit beträgt etwa 23 Jahre.

Standardfehler und Konfidenzintervallschätzungen der Überlebenswahrscheinlichkeiten

Diese Schätzungen der Überlebenswahrscheinlichkeiten zu bestimmten Zeitpunkten und der medianen Überlebenszeit sind Punktschätzungen und sollten als solche interpretiert werden. Es gibt Formeln zur Erstellung von Standardfehlern und Konfidenzintervallschätzungen von Überlebenswahrscheinlichkeiten, die mit vielen statistischen Berechnungspaketen erstellt werden können. Eine gängige Formel zur Schätzung des Standardfehlers der Überlebensschätzungen wird als Greenwoods5-Formel bezeichnet und lautet wie folgt:

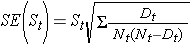
Die Menge 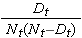wird für die Anzahl der Risikopersonen (Nt) und die Anzahl der Todesfälle (Dt), die bis zum interessierenden Zeitpunkt auftreten, summiert (d. h. kumulativ über alle Zeitpunkte vor dem interessierenden Zeitpunkt, siehe Beispiel in der Tabelle unten). Die Standardfehler werden für die Überlebensschätzungen für die Daten in der nachstehenden Tabelle berechnet. In der letzten Spalte ist die Größe 1,96*SE(St) angegeben, die die Fehlermarge darstellt und zur Berechnung der 95%-Konfidenzintervallschätzungen verwendet wird (d.h. St ± 1,96 x SE(St)).

Standardfehler der Überlebensschätzungen

Zeit, Jahre	Risikoanzahl Nt	Anzahl der Todesfälle Dt	Überlebens Wahrscheinlichkeit St				1.96*SE (St)
0	20		1
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0.000	0.118	0.174	0.341

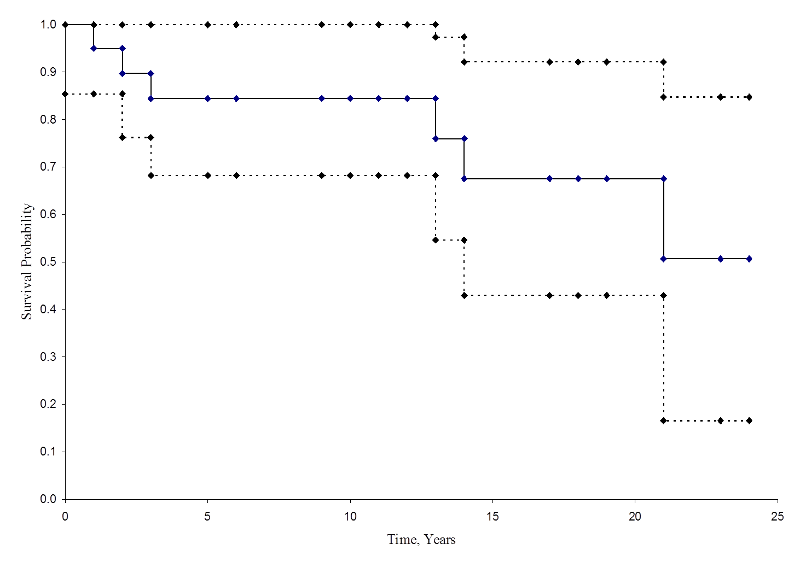
In der folgenden Abbildung sind die Schätzungen und Konfidenzintervalle zusammengefasst. Die Kaplan-Meier-Überlebenskurve ist als durchgezogene Linie dargestellt, und die 95%-Konfidenzgrenzen sind als gepunktete Linien angegeben.

Kaplan-Meier-Überlebenskurve mit Konfidenzintervallen

Kumulative Inzidenzkurven

Einige Forscher ziehen es vor, kumulative Inzidenzkurven zu erstellen, im Gegensatz zu Überlebenskurven, die die kumulativen Wahrscheinlichkeiten des Auftretens des interessierenden Ereignisses zeigen. Die kumulative Inzidenz bzw. die kumulative Ausfallwahrscheinlichkeit wird als 1-St berechnet und kann anhand der Lebensdauertabelle mit Hilfe des Kaplan-Meier-Ansatzes leicht ermittelt werden. Die kumulativen Ausfallwahrscheinlichkeiten für das obige Beispiel sind in der nachstehenden Tabelle aufgeführt.

Lebensdauertabelle mit kumulativen Ausfallwahrscheinlichkeiten

Zeit, Jahre	Anzahl der Risikopatienten Nt	Anzahl der Todesfälle Dt	Anzahl Zensiert Ct	Überlebenswahrscheinlichkeit St	Misserfolgswahrscheinlichkeit 1-St
0	20			1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0.493

Die folgende Abbildung zeigt die kumulative Inzidenz von Todesfällen für Teilnehmer, die an der oben beschriebenen Studie teilgenommen haben.

Kumulative Inzidenzkurve

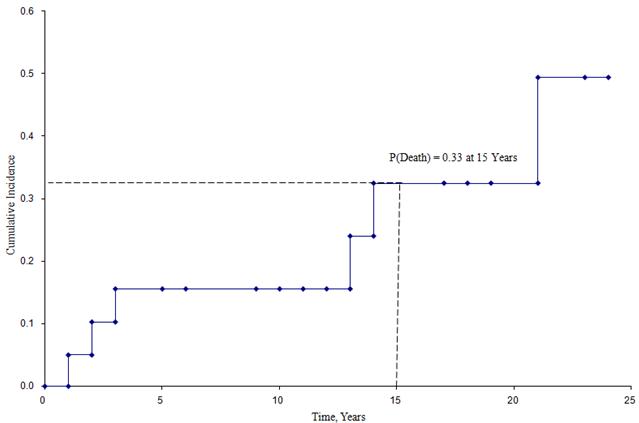
Aus dieser Abbildung lässt sich die Wahrscheinlichkeit abschätzen, dass ein Teilnehmer zu einem bestimmten Zeitpunkt stirbt. Zum Beispiel beträgt die Sterbewahrscheinlichkeit nach 15 Jahren etwa 33 % (siehe gestrichelte Linien).

Zum Anfang | vorherige Seite | nächste Seite