Tetraeder

Inhalt dieser Seite Was ist ein Tetraeder? Stücke des Tetraeders Tetraederzahlen Tetraeder im Würfel Ringe aus Tetraedern Tetraeder im Internet

Zur Hauptseite “Mathematische Basteleien”

Was ist ein Tetraeder?

Ein Tetraeder ist eine dreidimensionale Figur mit vier gleichschenkligen Dreiecken. Hebt man drei Dreiecke auf (1), erhält man das Tetraeder in der Draufsicht (2). Im Allgemeinen wird es in der Perspektive dargestellt (3).

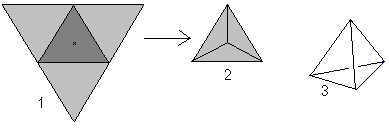
Wenn man das Wort Tetraeder betrachtet (Tetraeder bedeutet “mit vier Ebenen”), könnte man jede Pyramide mit einem Dreieck als Basis als Tetraeder bezeichnen.

Allerdings ist das Tetraeder auf dieser Seite die gerade, regelmäßige Dreieckspyramide.

Teile des Tetraeders
Höhe und Fläche eines seitlichen Dreiecks
Vier gleichseitige Dreiecke bilden ein Tetraeder.

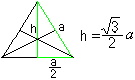…	Ein Dreieck wird herausgegriffen: Die drei Höhen schneiden sich wie in jedem Dreieck in einem Punkt. Dies ist der Mittelpunkt des Dreiecks. Die Höhe kann durch die Seite a als h=sqr(3)/2*a mit Hilfe des Satzes von Pythagoras berechnet werden.

Die Höhen sind auch Mittelpunkte und schneiden sich im Verhältnis2:1. Das wird in den folgenden Berechnungen verwendet.

Der Flächeninhalt des Dreiecks ist A=sqr(3)/4*a².

Raumhöhe

Die Höhe des Tetraeders liegt zwischen dem Mittelpunkt des Grunddreiecks (1) und dem Scheitelpunkt (2). Für die Berechnungen betrachtet man das so genannte Stützdreieck (3, gelb), das durch eine Kante und zwei Dreieckshöhen gebildet wird. Es gilt H=sqr(6)/3*a unter Anwendung des Pythagorasatzes.
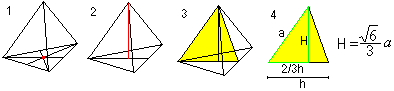
Mittelpunkt, umschriebeneKugel und eingeschriebene Kugel Der Mittelpunkt eines Tetraeders ist der Schnittpunkt zweier Raumhöhen (1,2,3). Er ist Schwerpunkt, Mittelpunkt der Kugel durch die vier Ecken und Mittelpunkt der größten Kugel, die noch in das Tetraeder passt (4).

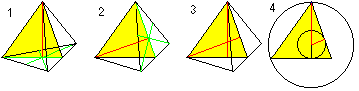
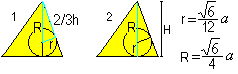…	Mit Hilfe desPythagoräischen Satzes (1) und H=R+r (2) erhält man zwei Formeln für r und R: Es gilt r=sqr(6)/12*a , R=sqr(6)/4*a.

Winkelfläche

….…..

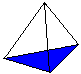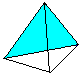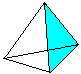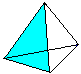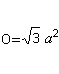Die Fläche der Grundfläche und die Seitenflächen bilden die FlächeO. Es gilt O=4*A (Dreieck) = sqr(3)a².

Volumen

Tetraederzahlen oben

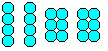……	Wenn man 20 Murmeln zu zwei Vierer- und zwei Sechser-Gruppen zusammenklebt, erhält man ein bekanntes Rätsel: Man muss eine Pyramide aus vier Teilen bilden.

Es gibt viele ähnliche Rätsel.

Tetraeder im Würfel oben
Sechs Flächendiagonalen bilden ein Tetraeder im Würfel.
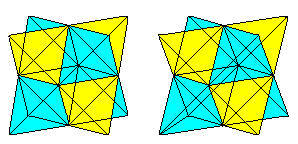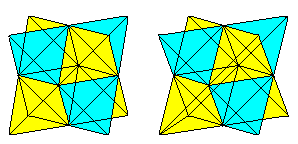
Wenn du die 3D-Ansicht kennst, kannst du die folgenden zwei Würfelpaare dreidimensional betrachten.

Das Volumen des Tetraeders ist der dritte Teil des Volumens des Würfels.

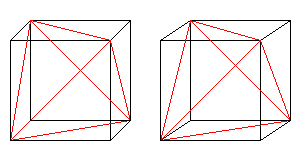
Zieht man ein zweites Tetraeder und die Schnittlinien, so erhält man eine Durchdringung von zwei Tetraedern.

Die Figur besteht aus den Flächendiagonalen und den Verbindungslinien der Mittelpunkte der Seitenquadrate des ursprünglichen Würfels. Die letzten Steine bilden ein Oktaeder.

Ringe aus Tetraedern nach oben
Man kann Papier-Tetraeder herstellen und eine gerade Anzahl davon auf einen Ring kleben. Der Ring kann sich durch die Mitte hindurch immer wieder nach innen oder nach außen drehen. Das ist ein hübsches Spielzeug. – Diese Ringe werden auch Kaleidozyklen genannt.

Tetraederauf dem Internettop

Deutsch

Christof Weber
Was ist dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

Englisch

Eric W. Weisstein (World of Mathematics)
Tetraeder

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

Joyce Frost und Peg Cagle (mathforum)
Ein erstaunlicher, raumfüllender, nicht-regulärer Tetraeder

Wikipedia
Tetraeder,Tetrapode(Struktur), Tetraederzahl