In “Krieg der Welten” tauchen riesige außerirdische Roboter aus dem Boden auf und beginnen, eine große Anzahl von Schauspielern zu verdampfen. An diesen Szenen gibt es viel zu mögen, aber es gibt drei Dinge, die ich nicht ausstehen konnte.
Die drei Beine, auf denen sie herumliefen. Nicht ihre zerbrechlich wirkende Spindeldürrheit, sondern ihre tatsächliche Dreibeinigkeit.
Bitte holt Tom Cruise zuerst, bitte holt Tom Cruise zuerst, bitte holt …
Es sollten mehr Beine sein. Ungefähr sechs, um genau zu sein.
“Sieh mal”, könntest du erwidern, “das ist ein außerirdisches Schiff, und wer weiß, was für Prinzipien die da entdeckt haben.”
Natürlich ist das möglich. Aber man kann es auch so sehen, dass wir Erdlinge eine große Vielfalt an Körper- und Gliedmaßenformen haben, und dennoch finden wir nirgendwo das Design mit drei Gliedmaßen. Vielleicht ist das ein gutes Argument dafür, dass Außerirdische kein Schiff mit drei Beinen bauen würden.
Was tun wir Erdlinge für die Gestaltung der Gliedmaßen?
Wir neigen dazu, einem Gesetz zu folgen, das sich durch alle Tiergruppen zieht, einem Gesetz, das ich erstmals 2001 im Journal of Theoretical Biology veröffentlicht und in meinem ersten Buch The Brain from 25,000 Feet näher erläutert habe.
Dieses “Gliedmaßengesetz” setzt die Anzahl der Gliedmaßen eines Tieres in Beziehung zur Länge dieser Gliedmaßen (im Verhältnis zur Körpergröße).
Wenn die Gliedmaßen eines Tieres im Verhältnis zur Körpergröße sehr lang sind, argumentierte ich, dass die optimale Lösung zum Ausstrecken (die die geringste Menge an “Draht” oder Gliedmaßenmaterial verbraucht) darin besteht, etwa sechs Gliedmaßen zu haben. (Dies gilt für Tiere mit Gliedmaßen, die annähernd radial um einen Umkreis ausgerichtet sind. Bei Tieren, deren Gliedmaßen gleichmäßig über eine Kugeloberfläche verteilt sind, beträgt die erwartete Anzahl der Gliedmaßen in diesem Fall etwa 12.)
Wenn die Gliedmaßen des Tieres im Verhältnis zur Körpergröße kürzer werden, steigt die erwartete Anzahl der Gliedmaßen, wobei die Anzahl der Gliedmaßen enorm ist, wenn die Gliedmaßen sehr kurz sind. (Eine Schlange hat übrigens unendlich viele unendlich kurze Gliedmaßen – also keine Gliedmaßen.)
Allgemeiner ausgedrückt, sagt das Gesetz voraus, dass die Anzahl der Gliedmaßen eines Tieres umgekehrt proportional zur relativen Gliedmaßenlänge ist. Und genauer gesagt, sagt das Gesetz eine bestimmte Proportionalitätskonstante voraus, so dass “sechs” die Lösung im Fall von wirklich langen Gliedmaßen ist.
Wenn L die Gliedmaßenlänge und R der Radius des Tierkörpers ist, dann ist k = L / (L + R) die relative Gliedmaßenlänge oder das “Gliedmaßenverhältnis”.
Die Anzahl der Gliedmaßen, N, dürfte ungefähr wie folgt variieren
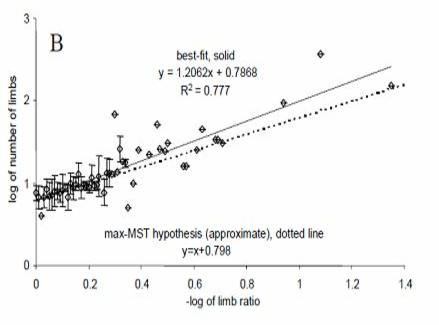
Die folgende Abbildung (aus meinem ersten Buch) zeigt, wie die Anzahl der Gliedmaßen tatsächlich mit dem Verhältnis der Gliedmaßen bei 190 Arten aus sieben Tiergruppen (Annelida, Arthropoda, Cnidaria, Echinodermata, Mollusca, Vertebrata und Tardigrada) zusammenhängt.
Der vorhergesagte Trend wird durch die durchgezogene Linie dargestellt, die mit der Gleichung N ≈ 6,28k-1 übereinstimmt, die wir gerade oben gesehen haben.
Der tatsächliche Trend ist mit der gepunkteten Linie dargestellt und führt zu einer empirischen Gleichung von N ≈6,24k-1,17 … oder sehr nahe an der Vorhersage.
Um einen besseren Eindruck vom Gliedmaßengesetz zu bekommen, dem Erdlinge zu folgen scheinen, sehen Sie sich dieses kleine dynamische visuelle Programm von Eric Bolz an, mit dem Sie die Länge der Gliedmaßen variieren und beobachten können, wie sich die Anzahl der Gliedmaßen verändert: http://www.changizi.com/limb.html Auf der rechten vertikalen Achse können Sie das Verhältnis der Gliedmaßen verändern und beobachten, wie sich die Anzahl der Gliedmaßen ändert. Die untere Achse erlaubt es, längere oder kürzere Kreaturen zu schaffen. Die linke vertikale Achse erlaubt es dir nur, die Größe der Kreatur auf der Seite zu verändern.
Die außerirdischen Schiffe aus Krieg der Welten sollten – angesichts ihrer langen Gliedmaßen und unter der Annahme, dass sie als ungefähr um einen Umfang herum zeigend behandelt werden sollten – etwa sechs Gliedmaßen haben. Nicht drei.
Deshalb sehen sie auch so albern aus. Sie befinden sich außerhalb des Sweetspots im Designraum für Gliedmaßen.
In meinem nächsten Beitrag werde ich erörtern, wie diese Gliedmaßen-Idee uns erklärt, warum wir 10 Finger haben, und vielleicht auch, warum wir ein Basis-10-Zahlensystem haben.