Graphes en Python

Origines de la théorie des graphes

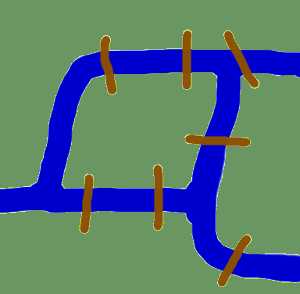Avant de commencer avec les implémentations réelles des graphes en Python et avant de commencer avec l’introduction de modules Python traitant des graphes, nous voulons nous consacrer aux origines de la théorie des graphes.
Les origines nous font remonter dans le temps jusqu’au Künigsberg du 18ème siècle. A cette époque, Königsberg était une ville de Prusse. La rivière Pregel traversait la ville, créant deux îles. La ville et les îles étaient reliées par sept ponts comme indiqué. Les habitants de la ville se demandaient s’il était possible de faire une promenade dans la ville en visitant chaque zone de la ville et en traversant chaque pont une seule fois. Chaque pont doit avoir été traversé complètement, c’est-à-dire qu’il n’est pas permis de marcher à mi-chemin sur un pont, puis de faire demi-tour et de traverser ensuite l’autre moitié depuis l’autre côté. Leonhard Euler a résolu le problème en 1735 en prouvant que ce n’était pas possible. Il a découvert que le choix d’un itinéraire à l’intérieur de chaque zone terrestre n’est pas pertinent et que la seule chose qui compte est l’ordre (ou la séquence) dans lequel les ponts sont traversés. Il avait formulé une abstraction du problème, en éliminant les faits inutiles et en se concentrant sur les zones terrestres et les ponts qui les relient. De cette façon, il a créé les bases de la théorie des graphes. Si nous voyons une “zone terrestre” comme un sommet et chaque pont comme une arête, nous avons “réduit” le problème à un graphe.

Introduction à la théorie des graphes à l’aide de Python

Avant de commencer notre traité sur les représentations possibles des graphes en Python, nous voulons présenter quelques définitions générales des graphes et de ses composants.
Un “graphe “1 en mathématiques et en informatique est constitué de “nœuds”, également appelés “sommets”.Les nœuds peuvent être connectés ou non les uns aux autres. Dans notre illustration, – qui est une représentation picturale d’un graphe, – le nœud “a” est connecté au nœud “c”, mais “a” n’est pas connecté à “b”. La ligne de connexion entre deux nœuds est appelée une arête. Si les arêtes entre les nœuds ne sont pas dirigées, le graphe est appelé un graphe non dirigé. Si une arête est dirigée d’un sommet (nœud) à un autre, le graphe est appelé un graphe dirigé. Une arête dirigée est appelée un arc.
Bien que les graphes puissent paraître très théoriques, de nombreux problèmes pratiques peuvent être représentés par des graphes. Ils sont souvent utilisés pour modéliser des problèmes ou des situations en physique, en biologie, en psychologie et surtout en informatique. En informatique, les graphes sont utilisés pour représenter les réseaux de communication, l’organisation des données, les dispositifs de calcul, le flux de calcul,

Dans ce dernier cas, les sont utilisés pour représenter l’organisation des données, comme le système de fichiers d’un système d’exploitation, ou les réseaux de communication. La structure des liens des sites Web peut également être considérée comme un graphe, c’est-à-dire un graphe dirigé, car un lien est une arête ou un arc dirigé.
Python ne possède pas de type de données ou de classe intégré pour les graphes, mais il est facile de les implémenter en Python. Un type de données est idéal pour représenter les graphes en Python, à savoir les dictionnaires. Le graphe de notre illustration peut être implémenté de la manière suivante :

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Les clés du dictionnaire ci-dessus sont les nœuds de notre graphe. Les valeurs correspondantes sont des listes avec les nœuds, qui sont reliés par un bord. Il n’y a pas de manière plus simple et plus élégante de représenter un graphe.
Un bord peut être vu comme un 2-tuple avec des nœuds comme éléments, c’est-à-dire (“a”, “b”)
Fonction pour générer la liste de tous les bords:Ce code génère la sortie suivante, si elle est combinée avec le dictionnaire de graphe défini précédemment:

 $ python3 graph_simple.py 

Comme nous pouvons le voir, il n’y a pas de bord contenant le nœud “f”. “f” est un nœud isolé de notre graphe.
La fonction Python suivante calcule les nœuds isolés d’un graphe donné:Si nous appelons cette fonction avec notre graphe, une liste contenant “f” sera retournée :

Graphes en tant que classe Python

Avant de poursuivre l’écriture de fonctions pour les graphes, nous avons un premier essai d’implémentation d’une classe de graphes Python. Si vous regardez le listing suivant de notre classe, vous pouvez voir dans la méthode __init__-méthode que nous utilisons un dictionnaire “self.__graph_dict” pour stocker les sommets et leurs sommets adjacents correspondants.
Si vous lancez ce module de manière autonome, vous obtiendrez le résultat suivant :

Paths in Graphs

Nous voulons maintenant trouver le plus court chemin d’un nœud à un autre nœud. Avant d’en venir au code Python de ce problème, il nous faut présenter quelques définitions formelles.
Vertices adjacents:
Deux sommets sont adjacents lorsqu’ils sont tous deux incidents à une arête commune.
Path dans un graphe non dirigé:
Un chemin dans un graphe non dirigé est une séquence de sommets P = ( v1, v2, ……., vn ) ∈ V x V x … x V telle que vi est adjacent à v{i+1} pour 1 ≤ i < n. Un tel chemin P est appelé un chemin de longueur n de v1 à vn.

Sentier simple:
Un chemin sans sommets répétés est appelé un chemin simple.
Exemple:
(a, c, e) est un chemin simple dans notre graphe, ainsi que (a,c,e,b). (a,c,e,b,c,d) est un chemin mais pas un chemin simple, parce que le nœud c apparaît deux fois.
La méthode suivante trouve un chemin d’un sommet de départ à un sommet d’arrivée:Si nous sauvegardons notre classe de graphe incluant la méthode find_path sous le nom de “graphs.py”, nous pouvons vérifier le mode de fonctionnement de notre fonction find_path:Le résultat du programme précédent ressemble à ceci :
La méthode find_all_paths trouve tous les chemins entre un sommet de départ et un sommet d’arrivée:Nous avons légèrement modifié notre exemple de graphe en ajoutant des arêtes de “a” à “f” et de “f” à “d” pour tester la méthode précédemment définie:Le résultat ressemble à ceci :

Degree

Le degré d’un sommet v dans un graphe est le nombre d’arêtes le reliant, les boucles étant comptées deux fois. Le degré d’un sommet v est noté deg(v). Le degré maximal d’un graphe G, noté Δ(G), et le degré minimal d’un graphe, noté δ(G), sont les degrés maximal et minimal de ses sommets.
Dans le graphe de droite, le degré maximal est 5 au sommet c et le degré minimal est 0, c’est-à-dire le sommet isolé f.
Si tous les degrés d’un graphe sont les mêmes, le graphe est un graphe régulier.Dans un graphe régulier, tous les degrés sont les mêmes, et on peut donc parler de degré du graphe.
La formule de la somme des degrés (lemme de Handshaking):
∑v &in ; Vdeg(v) = 2 |E|
Cela signifie que la somme des degrés de tous les sommets est égale au nombre d’arêtes multiplié par 2.On peut en conclure que le nombre de sommets de degré impair doit être pair. Cet énoncé est connu sous le nom de lemme du serrage de mains. Le nom “lemme de la poignée de main” provient d’un problème mathématique populaire : dans tout groupe de personnes, le nombre de personnes qui ont serré la main d’un nombre impair d’autres personnes du groupe est pair.
La méthode suivante calcule le degré d’un sommet :
La méthode suivante calcule une liste contenant les sommets isolés d’un graphe :
Les méthodes delta et Delta peuvent être utilisées pour calculer respectivement le degré minimum et maximum d’un sommet :

Séquence de degrés

La séquence de degrés d’un graphe non orienté est définie comme la séquence des degrés de ses sommets dans un ordre non croissant.
La méthode suivante retourne un tuple avec la séquence de degrés du graphe d’instance :
La séquence de degrés de notre graphe d’exemple est la séquence d’entiers suivante : (5,2,1,1,1,0).

Les graphes isomorphes ont la même séquence de degrés. Cependant, deux graphes ayant la même séquence de degrés ne sont pas nécessairement isomorphes.
Il y a la question de savoir si une séquence de degrés donnée peut être réalisée par un graphe asimple. Le théorème d’Erdös-Gallai stipule qu’une séquence non croissante de n nombres di (pouri = 1, …., n) est la séquence de degrés d’un graphe simple si et seulement si la somme de la séquence est paire et que la condition suivante est remplie:

Mise en œuvre du théorème d’Erdös-Gallai

Notre classe de graphes – voir plus bas pour une liste complète – contient une méthode “erdoes_gallai” qui décide, si une séquence remplit le théorème d’Erdös-Gallai. D’abord, on vérifie si la somme des éléments de la séquence est impaire. Si c’est le cas, la fonction renvoie False, car le théorème d’Erdös-Gallai ne peut plus être satisfait. Après cela, nous vérifions avec la méthode statique is_degree_sequence si la séquence d’entrée est une séquence de degrés, c’est-à-dire que les éléments de la séquence sont non croissants. C’est un peu superflu, puisque l’entrée est censée être une séquence de degré, donc vous pouvez laisser tomber cette vérification pour des raisons d’efficacité. Maintenant, nous vérifions dans le corps de la deuxième instruction if, si l’inéquation du théorème est remplie :
Version sans le test superflu de la séquence de degrés :

Densité du graphe

La densité du graphe est définie comme le rapport entre le nombre d’arêtes d’un graphe donné, et le nombre total d’arêtes, que le graphe pourrait avoir. En d’autres termes : Elle mesure à quel point un graphe donné est proche d’un graphe complet.
La densité maximale est de 1, si un graphe est complet. Ceci est clair, car le nombre maximal d’arêtes dans un graphe dépend des sommets et peut être calculé comme:
nombre maximal d’arêtes = ½ * |V| * ( |V| – 1 ).
D’autre part, la densité minimale est de 0, si le graphe n’a pas d’arêtes, c’est-à-dire que c’est un graphe isolé.
Pour les graphes simples non orientés, la densité du graphe est définie comme: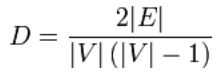

Un graphe dense est un graphe dans lequel le nombre d’arêtes est proche du nombre maximal d’arêtes. Un graphe avec seulement quelques arêtes, est appelé un graphe clairsemé. La définition de ces deux termes n’est pas très précise, c’est-à-dire qu’il n’y a pas de borne supérieure minimale (supremum) pour une densité clairsemée et pas de borne inférieure maximale (infimum) pour définir un graphe dense.
La notation mathématique la plus précise utilise la notation du grand O :

Graphe clairsemé :
Graphe dense :
Un graphe dense est un graphe G = (V, E) dans lequel |E| = Θ(|V|2).
“density” est une méthode de notre classe pour calculer la densité d’un graphe:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Nous pouvons tester cette méthode avec le script suivant. Un graphe complet a une densité de 1 et un graphe isolé a une densité de 0, comme nous pouvons le constater à partir des résultats du script de test précédent:

$ python test_density.py 0.4666666666671.00.0

Graphes connectés

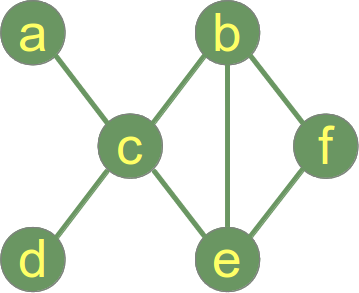Un graphe est dit connecté si chaque paire de sommets du graphe est connectée. L’exemple de graphe ci-contre est un graphe connecté.
Il est possible de déterminer avec un algorithme simple si un graphe est connecté :

1. Choisir un nœud arbitraire x du graphe G comme point de départ
2. Déterminer l’ensemble A de tous les nœuds qui peuvent être atteints à partir de x.
3. Si A est égal à l’ensemble des nœuds de G, le graphe est connecté, sinon il est déconnecté.

Nous implémentons une méthode is_connected pour vérifier si un graphe est un graphe connecté. Nous ne mettons pas l’accent sur l’efficacité mais sur la lisibilité.
Si vous ajoutez cette méthode à notre classe de graphe, nous pouvons la tester avec le script suivant. En supposant que vous enregistrez la classe de graphe sous le nom de graph2.py :
Une composante connectée est un sous-graphe connecté maximal de G. Chaque sommet appartient à exactement une composante connectée, tout comme chaque arête.

Distance et diamètre d’un graphe

La distance “dist” entre deux sommets dans un graphe est la longueur du plus court chemin entre ces sommets. Aucun retour en arrière, aucun détour, aucune boucle ne sont autorisés pour le calcul d’une distance.
Dans notre exemple de graphe à droite, la distance entre le sommet a et le sommet f est 3, c’est-à-dire dist(a,f) = 3, car le chemin le plus court passe par les sommets c et e (ou c et b alternativement).
L’excentricité d’un sommet s d’un graphe g est la distance maximale à tous les autres sommets du graphe :
e(s) = max( { dist(s,v) | v ∈ V })
(V est l’ensemble de tous les sommets de g)
Le diamètre d d’un graphe est défini comme l’excentricité maximale de tout sommet du graphe. Cela signifie que le diamètre est la longueur du chemin le plus court entre les nœuds les plus éloignés. Pour déterminer le diamètre d’un graphe, il faut d’abord trouver le chemin le plus court entre chaque paire de sommets. La plus grande longueur de n’importe lequel de ces chemins est le diamètre du graphe.

Nous pouvons directement voir dans notre graphe d’exemple que le diamètre est de 3, car la longueur minimale entre a et f est de 3 et il n’y a pas d’autre paire de sommets avec un chemin plus long.
La méthode suivante met en œuvre un algorithme pour calculer le diamètre. Nous pouvons calculer le diamètre de notre graphe d’exemple avec le script suivant, en supposant à nouveau, que notre classe de graphe complète est enregistrée sous le nom de graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Il imprimera la valeur 3.

La classe de graphe Python complète

Dans le code Python suivant, vous trouvez le module de classe Python complet avec toutes les methodes discutées:graph2.py

Arbre / Forêt

Un arbre est un graphe non orienté qui ne contient pas de cycles. Cela signifie que deux sommets quelconques du graphe sont reliés par exactement un chemin simple.
Une forêt est une union disjointe d’arbres. Contrairement aux forêts dans la nature, une forêt en théorie des graphes peut être constituée d’un seul arbre !
Un graphe avec un seul sommet et aucune arête est un arbre (et une forêt).
Un exemple d’arbre :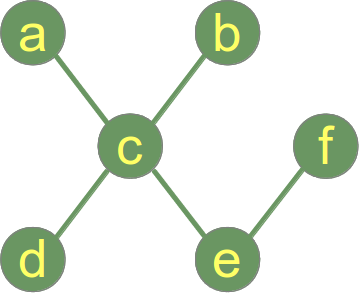

Alors que l’exemple précédent décrit un graphe qui est un arbre et une forêt, l’image suivante montre un graphe qui est constitué de deux arbres, c’est-à-dire que le graphe est une forêt mais pas un arbre.c’est-à-dire que le graphe est une forêt mais pas un arbre:

Aperçu des forêts:

Avec un sommet:

Graphes forestiers avec deux sommets :

Graphes forestiers avec trois sommets :

Arbre englobant

Un arbre englobant T d’un graphe connecté non orienté G est un sous-graphe G’ de G, qui est un arbre,et G’ contient tous les sommets et un sous-ensemble des arêtes de G. G’ contient toutes les arêtes de G, si G est un graphe arborescent. De manière informelle, un arbre englobant de G est une sélection d’arêtes de G qui forment un arbre englobant chaque sommet. C’est-à-dire que chaque sommet se trouve dans l’arbre, mais aucun cycle (ou boucle) n’est contenu.
Exemple:
Un graphe entièrement connecté: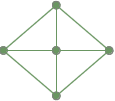

Deux arbres spanning du graphe entièrement connecté précédent :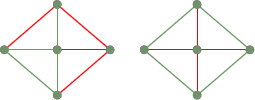

Jeu hamiltonien

Un chemin hamiltonien est un chemin dans un graphe non dirigé ou dirigé qui visite chaque sommet exactement une fois. Un cycle (ou circuit) hamiltonien est un chemin hamiltonien qui est un cycle.
Note pour les informaticiens : En général, il n’est pas possible de déterminer, si de tels chemins ou cycles existent dans des graphes arbitraires, car il a été prouvé que le problème du chemin hamiltonien est NP-complet.
Il est nommé d’après William Rowan Hamilton qui a inventé le soi-disant “jeu icosien”, ou le puzzle de Hamilton, qui consiste à trouver un cycle hamiltonien dans le graphe des arêtes du dodécaèdre. Hamilton a résolu ce problème en utilisant le calcul icosien, une structure algébrique basée sur des racines de l’unité présentant de nombreuses similitudes avec les quaternions, qu’il a également inventés.

Liste complète de la classe Graph

Nous pouvons tester cette classe Graph avec le programme suivant:Si nous lançons ce programme, nous obtenons la sortie suivante :
Notes de bas de page:
1 Les graphes étudiés en théorie des graphes (et dans ce chapitre de notre tutoriel Python) ne doivent pas être confondus avec les graphes des fonctions
2 Un singleton est un ensemble qui contient exactement un élément.
Crédits:
Narayana Chikkam, nchikkam(at)gmail(dot)com, a signalé une erreur d’indexation dans la méthode “erdoes_gallai”. Merci beaucoup, Narayana !