Dans le chapitre précédent, nous avons discuté des latches. Ce sont les blocs de construction de base des flip-flops. Nous pouvons implémenter les bascules de deux façons.
Dans la première méthode, il faut cascader deux latches de telle sorte que la première latche soit activée pour chaque impulsion d’horloge positive et la deuxième latche soit activée pour chaque impulsion d’horloge négative. De sorte que la combinaison de ces deux verrous devient une bascule.
Dans la deuxième méthode, nous pouvons directement mettre en œuvre la bascule, qui est sensible aux fronts. Dans ce chapitre, discutons des bascules suivantes en utilisant la deuxième méthode.
- Bascule SR
- Bascule D
- Bascule JK
- Bascule T
Bascule SR
La bascule SR fonctionne uniquement avec des transitions d’horloge positives ou des transitions d’horloge négatives. Alors que la bascule SR fonctionne avec le signal de validation. Le schéma de circuit de la bascule SR est montré dans la figure suivante.
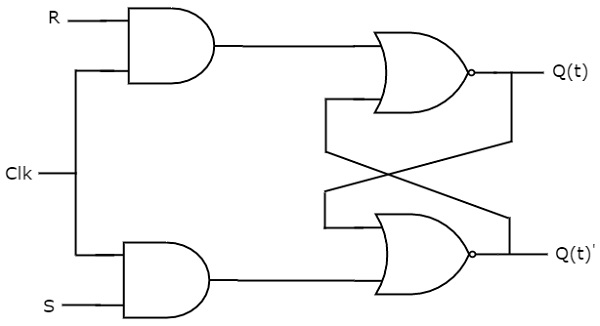
Ce circuit a deux entrées S & R et deux sorties Q(t) & Q(t)’. Le fonctionnement de la bascule SR est similaire à celui de la bascule SR. Mais, cette bascule affecte les sorties uniquement lorsqu’une transition positive du signal d’horloge est appliquée au lieu d’une activation active.
Le tableau suivant montre le tableau d’état de la bascule SR.
| S | Q(t + 1) | |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | – |
Ici, Q(t) & Q(t + 1) sont respectivement l’état actuel & l’état suivant. Ainsi, la bascule SR peut être utilisée pour une de ces trois fonctions telles que Hold, Reset & Set en fonction des conditions d’entrée, lorsque la transition positive du signal d’horloge est appliquée. Le tableau suivant montre le tableau des caractéristiques de la bascule SR.
| Entrées actuelles | État actuel | ||
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | x |
| 1 | 1 | 1 | x |
En utilisant trois variables K-Map, nous pouvons obtenir l’expression simplifiée de l’état suivant, Q(t + 1). La carte K à trois variables pour l’état suivant, Q(t + 1) est présentée dans la figure suivante.
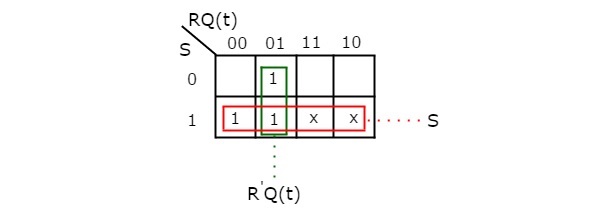
Les regroupements maximaux possibles des adjacents sont déjà présentés dans la figure. Par conséquent, l’expression simplifiée pour l’état suivant Q(t + 1) est
$Q\left ( t+1 \right )=S+{R}’Q\left ( t \right )$
D Flip-Flop
D flip-flop fonctionne avec seulement des transitions d’horloge positives ou des transitions d’horloge négatives. Alors que la bascule D fonctionne avec le signal de validation. Cela signifie que la sortie de la bascule D est insensible aux changements de l’entrée, D sauf pour la transition active du signal d’horloge. Le schéma de circuit de la bascule D est présenté dans la figure suivante.
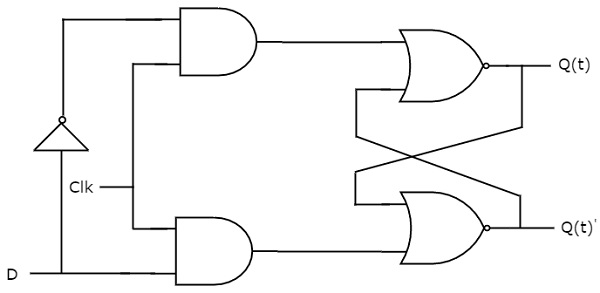
Ce circuit a une seule entrée D et deux sorties Q(t) & Q(t)’. Le fonctionnement de la bascule D est similaire à celui de la bascule D. Mais, cette bascule affecte les sorties seulement lorsque la transition positive du signal d’horloge est appliquée au lieu de l’activation active.
Le tableau suivant montre le tableau d’état de la bascule D.
| D | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Par conséquent, La bascule D maintient toujours l’information, qui est disponible sur l’entrée de données, D de la transition positive antérieure du signal d’horloge. A partir du tableau d’état ci-dessus, nous pouvons directement écrire l’équation de l’état suivant comme
Q(t + 1) = D
L’état suivant de la bascule D est toujours égal à l’entrée de données, D pour chaque transition positive du signal d’horloge. Par conséquent, les bascules D peuvent être utilisées dans les registres, les registres à décalage et certains des compteurs.
Bascule JK
La bascule JK est la version modifiée de la bascule SR. Elle fonctionne uniquement avec des transitions d’horloge positives ou des transitions d’horloge négatives. Le schéma de circuit de la bascule JK est montré dans la figure suivante.
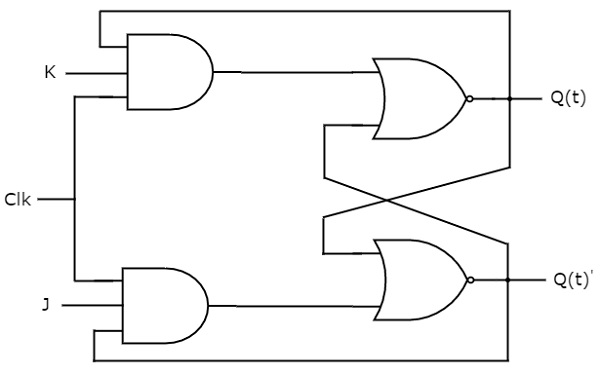
Ce circuit a deux entrées J & K et deux sorties Q(t) & Q(t)’. Le fonctionnement de la bascule JK est similaire à celui de la bascule SR. Ici, nous avons considéré les entrées de la bascule SR comme S = J Q(t)’ et R = KQ(t) afin d’utiliser la bascule SR modifiée pour 4 combinaisons d’entrées.
Le tableau suivant montre la table d’état de la bascule JK.
| J | Q(t + 1) | |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q(t)’ |
Ici, Q(t) & Q(t + 1) sont respectivement l’état actuel & l’état suivant. Ainsi, la bascule JK peut être utilisée pour l’une de ces quatre fonctions telles que Hold, Reset, Set & Complément de l’état présent en fonction des conditions d’entrée, lorsque la transition positive du signal d’horloge est appliquée. Le tableau suivant montre le tableau des caractéristiques de la bascule JK.
| Entrées actuelles | État actuel | ||
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
En utilisant trois variables K-Map, nous pouvons obtenir l’expression simplifiée de l’état suivant, Q(t + 1). La carte K à trois variables pour l’état suivant, Q(t + 1) est présentée dans la figure suivante.
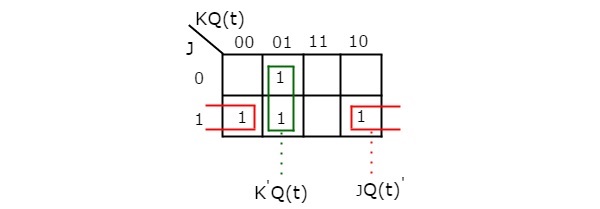
Les regroupements maximaux possibles des adjacents sont déjà présentés dans la figure. Par conséquent, l’expression simplifiée pour le prochain état Q(t+1) est
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}’+{K}’Q\left ( t \right )$$
T Flip-Flop
T flip-flop est la version simplifiée de JK flip-flop. Elle est obtenue en connectant la même entrée ‘T’ aux deux entrées de la bascule JK. Elle fonctionne uniquement avec des transitions d’horloge positives ou des transitions d’horloge négatives. Le schéma de circuit de la bascule T est présenté dans la figure suivante.
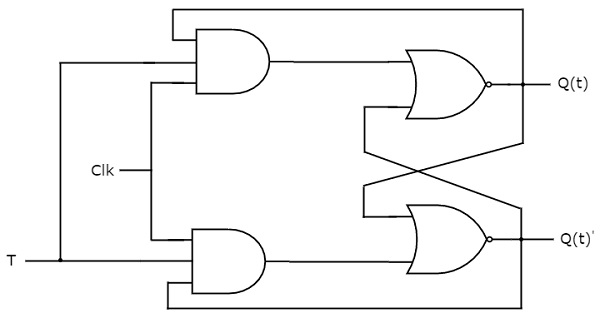
Ce circuit a une seule entrée T et deux sorties Q(t) & Q(t)’. Le fonctionnement de la bascule T est le même que celui de la bascule JK. Ici, nous avons considéré les entrées de la bascule JK comme J = T et K = T afin d’utiliser la bascule JK modifiée pour 2 combinaisons d’entrées. Ainsi, nous avons éliminé les deux autres combinaisons de J & K, pour lesquelles ces deux valeurs sont complémentaires l’une de l’autre dans la bascule T.
Le tableau suivant montre la table d’état de la bascule T.
| D | Q(t + 1) |
|---|---|
| 0 | Q(t) |
| 1 | Q(t)’ |
Ici, Q(t) & Q(t + 1) sont respectivement l’état actuel & l’état suivant. Ainsi, la bascule T peut être utilisée pour l’une de ces deux fonctions telles que Hold, & Complément de l’état présent en fonction des conditions d’entrée, lorsque la transition positive du signal d’horloge est appliquée. Le tableau suivant montre le tableau des caractéristiques de la bascule T.
| État actuel | |||
|---|---|---|---|
| T | Q(t) | Q(t + 1) | |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
D’après le tableau caractéristique ci-dessus, nous pouvons directement écrire l’équation d’état suivante comme
$$Q\left ( t+1 \right )={T}’Q\left ( t \right )+TQ{\left ( t \right )}’$$
$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
La sortie de la bascule Tbascule toujours pour chaque transition positive du signal d’horloge, lorsque l’entrée T reste au niveau logique haut (1). Par conséquent, la bascule T peut être utilisée dans les compteurs.
Dans ce chapitre, nous avons implémenté diverses bascules en fournissant le couplage croisé entre les portes NOR. De même, vous pouvez mettre en œuvre ces bascules en utilisant des portes NAND.
.