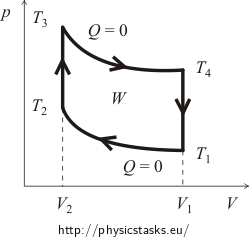
Au début, il est généralement nécessaire de se faire une idée du diagramme pV du cycle. Pour cela nous allons tracer les courbes des processus isochoriques et adiabatiques. Le graphique approximatif du cycle d’Otto est représenté sur la figure suivante.
Le rendement η du cycle est défini comme suit
\
où W est le travail effectué par le gaz pendant un cycle moins le travail effectué par les forces extérieures (dans le diagramme, il est représenté par la surface de l’aire définie par les lignes du cycle !) et Qsup est la chaleur fournie au système pendant le cycle.
Le travail W peut être calculé en utilisant la relation entre la pression et le volume pendant une expansion et une compression adiabatiques (le travail effectué pendant un processus isochore est bien sûr nul). Dans cette tâche, cependant, il sera préférable d’utiliser le fait que la variation totale de l’énergie interne par cycle doit être égale à zéro (on revient au même état qu’au début, donc la température et donc l’énergie interne restent les mêmes !) Selon la première loi de la thermodynamique, le travail effectué par le gaz peut être exprimé comme la différence entre la chaleur Qsup fournie et la chaleur Qrel libérée. La formule du rendement du cycle est donc de la forme
\
Dans un premier temps, nous allons calculer la chaleur fournie Qsup. Il est clair que pendant le processus adiabatique il n’y a pas d’échange de chaleur et pendant le refroidissement isochore la chaleur est libérée. Cela signifie que la chaleur sera fournie uniquement pendant le chauffage isochore de la température T2 à la température T3. La quantité de cette chaleur peut être exprimée dans les variables de la quantité de substance n du gaz et de sa capacité thermique molaire CV comme suit :
\
Nous exprimerons la quantité de chaleur libérée Qrel à peu près de la même manière. Nous savons déjà que la chaleur est libérée uniquement lors du refroidissement isochore de la température T4 vers la température initiale T1. Il est vrai que :
\
Nous substituons maintenant ces formules dans la formule du rendement du cycle et nous obtenons immédiatement :
\
Nous allons maintenant devoir exprimer les différences de température en utilisant le taux de compression donné
\
et le coefficient de Poisson κ.
Pour ce faire, nous utiliserons l’équation d’un gaz idéal subissant un processus adiabatique (la loi de Poisson) pVκ = C = konst…, où C est une constante. Nous évaluons maintenant la pression à partir de l’équation d’état d’un gaz idéal
\
que nous substituons à la loi de Poisson. Maintenant nous transférons les constantes (C et K) d’un côté
\
Maintenant nous appliquons cette loi de Poisson pour les deux processus adiabatiques. Pour l’expansion adiabatique nous obtenons la relation
\
Et pour la compression adiabatique nous obtenons
\
Maintenant nous soustrayons la deuxième équation de la première et factorisons V1κ – 1 d’un côté et V2κ – 1 de l’autre. Nous obtenons :
\ \
Nous pouvons voir que nous avons effectivement réussi à exprimer les différences de température en utilisant les valeurs données. Maintenant, nous substituons cette relation dans la formule du rendement et nous obtenons l’équation finale:
\ \ \.