Par Evan Ma

(tuteur en mathématiques et en physique au centre d’apprentissage The Edge)

La fonction logarithmique semble déconcerter de nombreux élèves étudiant le programme IB Math SL. Afin de bien la comprendre, définissons

où , un nombre réel strictement positif, est appelé la base et est la puissance. Par exemple, nous connaissons tous par cœur la suite :

et ainsi de suite. La fonction logarithmique le fait à l’envers – étant donné un nombre comme argument, elle donne la puissance soumise à une base spécifiée, et donc elle est définie comme suit .

Si

alors

Il est donc clair que

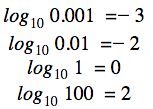
et ainsi de suite. Voyons d’autres exemples impliquant d’autres bases :

Répondons aux questions suivantes pour nous entraîner : (a) , (b) , (c) , (d) . Les réponses se trouvent à la fin de ce blog.

De la définition du logarithme, on peut aussi voir que si on élève la base par le base-logarithme d’un nombre réel , on retrouvera le nombre , viz

Vous pouvez essayer de vérifier cela en utilisant votre calculatrice pour différentes bases valides. Cette identité est importante lorsque nous essayons de résoudre des équations logarithmiques, dont des exemples seront donnés alter.

Maintenant, jetons un coup d’œil aux règles du logarithme. Comme pour la définition du logarithme, nous utilisons les lois des indices pour dériver les règles :

1. Le logarithme d’un produit est la somme des logarithmes

Preuve : Dites et , donc

2. Le logarithme de base de Monsieur est fois

Proof : Dites , donc

3. Le logarithme d’un quotient est la différence des logarithmes

Preuve : Disons et , donc

4. La dernière règle s’appelle la formule de changement de base. Nous allons utiliser un exemple comme outil pour dériver la formule. Disons que nous voulons savoir à quelle puissance il faut élever 2 pour obtenir 50. Comme 50 n’est pas une puissance entière de 2, la réponse n’est pas très évidente. On écrit donc

et donc. Pour trouver , disons que nous appliquons le logarithme en base 10 aux deux côtés de l’équation car notre calculatrice peut ne pas avoir la touche logarithme en base 2 :

Corrigée à 4 chiffres significatifs, la valeur de est approximativement 5,644. En fait, vous pouvez vérifier votre réponse en élevant 2 à la puissance de 5,644 pour voir que la réponse est approximativement 50.

Pour généraliser le problème, disons que nous devons trouver tel que et que le logarithme de base- n’est pas à notre disposition, nous pouvons donc à la place utiliser le logarithme de base- selon l’équation

et donc

À titre d’exemple, considérons ce qui suit. Supposons qu’une somme de 10 000 $ soit déposée à un taux d’intérêt de 2,5 % par an, composé annuellement. Combien de temps l’argent doit-il être conservé sur le compte pour qu’il atteigne 50 000 $ ?

Pour répondre à la question, nous essayons essentiellement de trouver n tel que

Comme ma simple calculatrice scientifique ne me permet pas de spécifier une base de 1.025 pour la clé logarithmique, je vais devoir me fier à la formule de changement de base et utiliser la base 10, et donc

Puisque les intérêts sont composés annuellement, il faudra 66 ans pour qu’ils croissent au moins 5 fois.

Ayant exploré les règles des logarithmes, nous introduisons la fonction logarithmique naturelle, ou . Elle est base-, où est l’éminent nombre irrationnel ≈2,71828 et dont on ne soulignera jamais assez l’importance en sciences et en mathématiques. Par conséquent, le logarithme de base- est défini comme suit.

Si

alors

Présentons ensuite deux exemples où des erreurs courantes sont commises dans la résolution d’équations de logarithmes. Voyez si vous pouvez identifier l’erreur.

Où est l’erreur ? Regardez de plus près. Bien sûr, dans la deuxième étape, on ne peut pas “diviser” le logarithme à travers le signe d’addition. Rappelez-vous, vous ne pouvez “diviser” un logarithme en une somme que si le logarithme est appliqué à un produit, et non à une somme. Les étapes correctes sont donc les suivantes:

Maintenant, regardons l’exemple suivant, et voyons si vous pouvez identifier l’erreur:

Où est l’erreur ? Oui, elle est dans la deuxième étape – un quotient de logarithmes n’est bien sûr pas le logarithme du quotient. Nous pouvons plutôt utiliser la formule de changement de base pour simplifier la première étape, comme suit :

Enfin, nous allons illustrer comment utiliser les règles du logarithme pour résoudre ce qui suit :

Vous pouvez remarquer que l’inconnue apparaît comme base et comme variable dans l’argument du logarithme. Comment pouvons-nous résoudre ? La méthode dépend encore de l’application cohérente des règles du logarithme. Tout d’abord, nous élevons les deux côtés en tant que puissances de la base , et donc

Vous pouvez vous rappeler de la définition du logarithme que le côté gauche deviendra juste l’argument du logarithme, et donc

En réarrangeant l’équation ci-dessus, nous devons résoudre

Notant que cela ressemble à un quadratique en , nous résolvons comme suit :

Maintenant, où est la racine négative ? Puisque est aussi la base du logarithme, la racine négative est donc rejetée comme solution. Par conséquent, est la réponse finale.

En examinant les exemples ci-dessus, vous pouvez voir que la résolution d’une équation logarithmique apparemment difficile n’est pas du tout difficile – il suffit d’appliquer les règles du logarithme de manière cohérente et la solution correcte peut être obtenue.

Réponses aux questions : (a) 2 (b) 3 (c) -3 (d) -2.