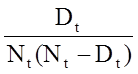Il existe plusieurs façons différentes d’estimer une fonction de survie
ou une courbe de survie. Il existe un certain nombre de méthodes paramétriques populaires qui sont utilisées pour modéliser les données de survie, et elles diffèrent en termes d’hypothèses faites sur la distribution des temps de survie dans la population. Parmi les distributions populaires, on trouve les distributions exponentielle, de Weibull, de Gompertz et log-normale.2 La plus populaire est sans doute la distribution exponentielle, qui suppose que la probabilité pour un participant de subir l’événement en question est indépendante de la durée pendant laquelle il n’a pas subi d’événement. D’autres distributions font différentes hypothèses sur la probabilité qu’un individu développe un événement (c’est-à-dire qu’elle peut augmenter, diminuer ou changer avec le temps). Vous trouverez plus de détails sur les méthodes paramétriques d’analyse de survie dans Hosmer et Lemeshow et Lee et Wang1,3.
Nous nous concentrons ici sur deux méthodes non paramétriques, qui ne font aucune hypothèse sur la façon dont la probabilité qu’une personne développe l’événement change au fil du temps. En utilisant des méthodes non paramétriques, nous estimons et traçons la distribution de survie ou la courbe de survie. Les courbes de survie sont souvent représentées sous forme de fonctions à échelons, comme le montre la figure ci-dessous. Le temps est indiqué sur l’axe des X et la survie (proportion de personnes à risque) est indiquée sur l’axe des Y. Notez que le pourcentage de participants qui survivent ne représente pas toujours le pourcentage de ceux qui sont en vie (ce qui suppose que l’issue d’intérêt est le décès). “La survie” peut également faire référence à la proportion qui est exempte d’un autre événement de résultat (par exemple, le pourcentage d’absence d’infarctus ou de maladie cardiovasculaire), ou elle peut également représenter le pourcentage qui ne connaît pas de résultat sain (par exemple, une rémission du cancer).
Fonction de survie
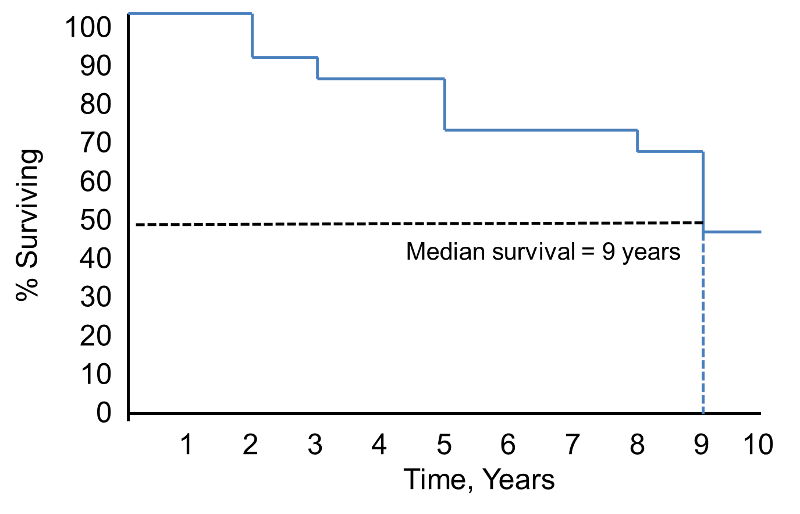
Notez que la probabilité de survie est de 100% pendant 2 ans puis chute à 90%. La survie médiane est de 9 ans (c’est-à-dire que 50 % de la population survit 9 ans ; voir les lignes pointillées).
Exemple:
Envisagez une petite étude de cohorte prospective conçue pour étudier le temps jusqu’au décès. L’étude porte sur 20 participants âgés de 65 ans et plus ; ils sont inscrits sur une période de 5 ans et sont suivis jusqu’à 24 ans, jusqu’à leur décès, la fin de l’étude ou leur abandon de l’étude (perdus de vue). Les données sont présentées ci-dessous. Dans l’étude, il y a 6 décès et 3 participants avec un suivi complet (c’est-à-dire 24 ans). Les 11 autres ont moins de 24 ans de suivi en raison d’une inscription tardive ou d’une perte de suivi.
|
Numéro d’identification du participant |
Année de décès |
Année de dernier contact |
|---|---|---|
|
1 |
|
24 |
|
2 |
3 |
|
|
3 |
|
11 |
|
4 |
|
19 |
|
5 |
|
24 |
|
6 |
|
13 |
|
7 |
14 |
|
|
8 |
|
2 |
|
9 |
|
18 |
|
10 |
|
17 |
|
11 |
|
24 |
|
12 |
|
21 |
|
13 |
|
12 |
|
14 |
1 |
|
|
15 |
|
10 |
|
16 |
23 |
|
|
17 |
|
6 |
|
18 |
5 |
|
|
19 |
|
9 |
|
20 |
17 |
|
Tableau de vie (tableau actuariel)
Une façon de résumer les expériences des participants est avec un tableau de vie, ou une table actuarielle. Les tables de vie sont souvent utilisées dans le secteur de l’assurance pour estimer l’espérance de vie et fixer les primes. Nous nous concentrons sur un type particulier de table de mortalité, largement utilisé dans l’analyse biostatistique, appelé table de mortalité de cohorte ou table de mortalité de suivi. La table de survie de suivi résume les expériences des participants au cours d’une période de suivi prédéfinie dans une étude de cohorte ou dans un essai clinique jusqu’au moment de l’événement d’intérêt ou la fin de l’étude, selon ce qui se produit en premier.
Pour construire une table de survie, nous organisons d’abord les temps de suivi en intervalles équidistants. Dans le tableau ci-dessus, nous avons un suivi maximum de 24 ans, et nous considérons des intervalles de 5 ans (0-4, 5-9, 10-14, 15-19 et 20-24 ans). Nous additionnons le nombre de participants qui sont vivants au début de chaque intervalle, le nombre de ceux qui meurent et le nombre de ceux qui sont censurés dans chaque intervalle.
|
Intervalle en années |
Nombre de vivants au début de l’intervalle |
Nombre de décès pendant l’intervalle |
Nombre censuré |
|---|---|---|---|
|
0-.4 |
20 |
2 |
1 |
|
5-9 |
17 |
1 |
2 |
|
10-14 |
14 |
1 |
4 |
|
15-19 |
9 |
1 |
3 |
|
20-24 |
5 |
1 |
4 |
Nous utilisons la notation suivante dans notre analyse des tables de survie. Nous définissons d’abord la notation et l’utilisons ensuite pour construire la table de survie.
- Nt = nombre de participants qui sont sans événement et considérés à risque pendant l’intervalle t (par ex, dans cet exemple, le nombre de personnes en vie puisque notre résultat d’intérêt est le décès)
- Dt = nombre de participants qui meurent (ou subissent l’événement d’intérêt) pendant l’intervalle t
- Ct = nombre de participants qui sont censurés pendant l’intervalle t Nt* = le nombre moyen de participants à risque pendant l’intervalle t
- Nt* = le nombre moyen de participants à risque pendant l’intervalle t [Dans la construction des tables de mortalité actuarielles, les hypothèses suivantes sont souvent faites : Premièrement, les événements d’intérêt (par exemple, les décès) sont supposés se produire à la fin de l’intervalle et les événements censurés sont supposés se produire de manière uniforme (ou égale) tout au long de l’intervalle. Par conséquent, un ajustement est souvent apporté à Nt pour refléter le nombre moyen de participants à risque pendant l’intervalle, Nt*, qui est calculé comme suit : Nt* =Nt-Ct/2 (c’est-à-dire, nous soustrayons la moitié des événements censurés).
- qt = proportion de décès (ou d’événement souffrant) pendant l’intervalle t, qt = Dt/Nt*
- pt = proportion de survie (restant sans événement) pendant l’intervalle t, pt = 1-qt
- St, la proportion de survie (ou restant sans événement) après l’intervalle t ; on l’appelle parfois la probabilité de survie cumulative et elle est calculée comme suit : Tout d’abord, la proportion de participants survivant après le temps 0 (le temps de départ) est définie comme S0 = 1 (tous les participants vivants ou sans événement au temps zéro ou au début de l’étude). La proportion de participants ayant survécu à chaque intervalle ultérieur est calculée à l’aide des principes de probabilité conditionnelle présentés dans le module sur les probabilités. Plus précisément, la probabilité qu’un participant survive à l’intervalle 1 est S1 = p1. La probabilité qu’un participant survive à l’intervalle 2 signifie qu’il a dû survivre à l’intervalle 1 et à l’intervalle 2 : S2 = P(survivre à l’intervalle 2) = P(survivre à l’intervalle 2)*P(survivre à l’intervalle 1), ou S2 = p2*S1. En général, St+1 = pt+1*St.
Le format de la table de suivi de la vie est indiqué ci-dessous.
Pour le premier intervalle, 0-4 ans : Au temps 0, le début du premier intervalle (0-4 ans), il y a 20 participants vivants ou à risque. Deux participants meurent dans l’intervalle et 1 est censuré. Nous appliquons la correction pour le nombre de participants censurés pendant cet intervalle pour obtenir Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Les calculs des autres colonnes sont présentés dans le tableau. La probabilité qu’un participant survive au-delà de 4 ans, ou au-delà du premier intervalle (en utilisant la limite supérieure de l’intervalle pour définir le temps) est S4 = p4 = 0,897.
Pour le second intervalle, 5-9 ans : Le nombre à risque est le nombre à risque dans l’intervalle précédent (0-4 ans) moins ceux qui meurent et sont censurés (c’est-à-dire Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). La probabilité qu’un participant survive au-delà de 9 ans est S9 = p9*S4 = 0,937*0,897 = 0,840.
|
Intervalle en années |
Nombre à risque pendant l’intervalle, Nt |
Nombre moyen à risque pendant l’intervalle, Nt* |
Nombre de décès pendant l’intervalle, Dt |
Perdus au suivi, Ct |
Proportion de décès pendant l’intervalle, qt |
Parmi les personnes à risque, proportion de survivants Intervalle, pt |
Probabilité de survie St |
|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
20-(1/2) = 19.5 |
2 |
1 |
2/19.5 = 0.103 |
1-0.103 = 0.897 |
1(0.897) = 0.897 |
|
5-9 |
17 |
17-(2/2) = 16.0 |
1 |
2 |
1/16 = 0.063 |
1-0.063 = 0.937 |
(0,897)(0,937)=0,840 |
La table de suivi de vie complète est présentée ci-dessous.
|
Intervalle en années |
Nombre à risque pendant l’intervalle, Nt |
Nombre moyen à risque pendant l’intervalle, Nt* |
Nombre de décès pendant l’intervalle, Dt |
Perdus au suivi, Ct |
Proportion de décès pendant l’intervalle, qt |
Parmi les personnes à risque, Proportion de survivants Intervalle, pt |
Probabilité de survie St |
|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
19.5 |
2 |
1 |
0.103 |
0.897 |
0.897 |
|
5-9 |
17 |
16.0 |
1 |
2 |
0.063 |
0.937 |
0.840 |
|
10-14 |
14 |
12.0 |
1 |
4 |
0.083 |
0.917 |
0.770 |
|
15-19 |
9 |
7.5 |
1 |
3 |
0.133 |
0.867 |
0.668 |
|
20-24 |
5 |
3.0 |
1 |
4 |
0.333 |
0,667 |
0,446 |
Cette table utilise la méthode actuarielle pour construire la table de suivi de la vie où le temps est divisé en intervalles équidistants.
Approche de Kaplan-Meier (limite de produit)
Un problème avec l’approche de la table de survie présentée ci-dessus est que les probabilités de survie peuvent changer selon la façon dont les intervalles sont organisés, en particulier avec de petits échantillons. L’approche de Kaplan-Meier, également appelée approche produit-limite, est une approche populaire qui résout ce problème en réestimant la probabilité de survie chaque fois qu’un événement se produit.
L’utilisation appropriée de l’approche de Kaplan-Meier repose sur l’hypothèse que la censure est indépendante de la probabilité de développer l’événement d’intérêt et que les probabilités de survie sont comparables chez les participants qui sont recrutés tôt et plus tard dans l’étude. Lorsque l’on compare plusieurs groupes, il est également important que ces hypothèses soient satisfaites dans chaque groupe de comparaison et que, par exemple, la censure ne soit pas plus probable dans un groupe que dans un autre.
Le tableau ci-dessous utilise l’approche de Kaplan-Meier pour présenter les mêmes données que celles présentées ci-dessus à l’aide de l’approche des tables de survie. Notez que nous commençons le tableau avec le temps=0 et la probabilité de survie = 1. Au temps=0 (ligne de base, ou début de l’étude), tous les participants sont à risque et la probabilité de survie est de 1 (ou 100%). Avec l’approche de Kaplan-Meier, la probabilité de survie est calculée en utilisant St+1 = St*((Nt+1-Dt+1)/Nt+1). Notez que les calculs utilisant l’approche Kaplan-Meier sont similaires à ceux utilisant l’approche des tables de survie actuarielles. La principale différence réside dans les intervalles de temps, c’est-à-dire qu’avec l’approche des tables de survie actuarielles, nous considérons des intervalles équidistants, tandis qu’avec l’approche de Kaplan-Meier, nous utilisons des temps d’événements observés et des temps de censure. Les calculs des probabilités de survie sont détaillés dans les premières lignes du tableau.
Tableau de survie utilisant l’approche de Kaplan-Meier
|
Temps, Années |
Nombre à risque Nt |
Nombre de décès Dt . |
Nombre de censurés Ct |
Probabilité de survie St+1 = St*((Nt+1-Dt+1)/Nt+1) |
|---|---|---|---|---|
|
0 |
20 |
|
|
1 |
|
1 |
20 |
1 |
|
1*((20-1)/20) = 0.950 |
|
2 |
19 |
|
1 |
0.950*((19-0)/19)=0.950 |
|
3 |
18 |
1 |
|
0.950*((18-1)/18) = 0.897 |
|
5 |
17 |
1 |
|
0.897*((17-1)/17) = 0.844 |
|
6 |
16 |
|
1 |
0.844 |
|
9 |
15 |
|
1 |
0.844 |
|
10 |
14 |
|
1 |
0.844 |
|
11 |
13 |
|
1 |
0.844 |
|
12 |
12 |
|
1 |
0.844 |
|
13 |
11 |
|
1 |
0.844 |
|
14 |
10 |
1 |
|
0.760 |
|
17 |
9 |
1 |
1 |
0.676 |
|
18 |
7 |
|
1 |
0.676 |
|
19 |
6 |
|
1 |
0.676 |
|
21 |
5 |
|
1 |
0.676 |
|
23 |
4 |
1 |
|
0.507 |
|
24 |
3 |
|
3 |
0,507 |
Avec de grands ensembles de données, ces calculs sont fastidieux. Cependant, ces analyses peuvent être générées par des programmes de calcul statistique comme SAS. Excel peut également être utilisé pour calculer les probabilités de survie une fois que les données sont organisées par temps et que les nombres d’événements et de temps censurés sont résumés.
À partir de la table de survie, nous pouvons produire une courbe de survie de Kaplan-Meier.
Courbe de survie de Kaplan-Meier pour les données ci-dessus
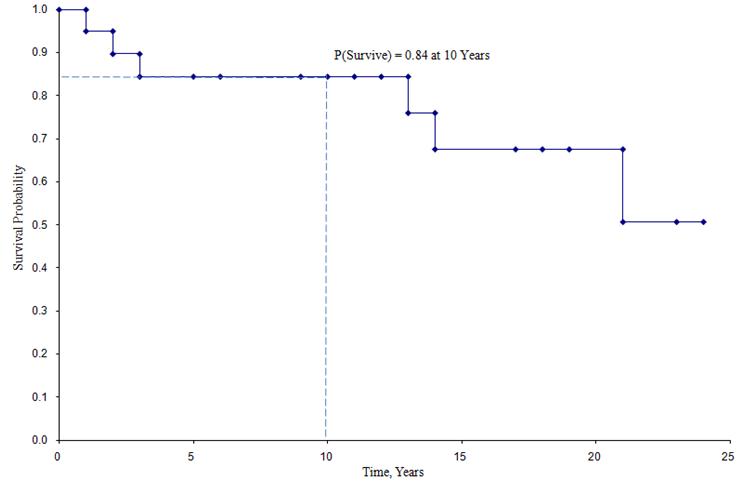
Dans la courbe de survie présentée ci-dessus, les symboles représentent chaque temps d’événement, soit un décès, soit un temps censuré. A partir de la courbe de survie, nous pouvons également estimer la probabilité qu’un participant survive au-delà de 10 ans en localisant 10 ans sur l’axe des X et en lisant vers le haut et vers l’axe des Y. La proportion de participants survivant après 10 ans est de 84%, et la proportion de participants survivant après 20 ans est de 68%. La survie médiane est estimée en plaçant 0,5 sur l’axe des Y et en lisant vers le haut et vers le bas sur l’axe des X. La survie médiane est d’environ 23 ans. La survie médiane est d’environ 23 ans.
Erreurs types et estimations de l’intervalle de confiance des probabilités de survie
Ces estimations des probabilités de survie à des moments précis et de la durée médiane de survie sont des estimations ponctuelles et doivent être interprétées comme telles. Il existe des formules pour produire des erreurs standard et des estimations de l’intervalle de confiance des probabilités de survie qui peuvent être générées avec de nombreux progiciels de calcul statistique. Une formule populaire pour estimer l’erreur standard des estimations de survie est appelée formule de Greenwoods5 et est la suivante :
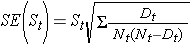
La quantité 
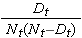est additionnée pour les nombres à risque (Nt) et les nombres de décès (Dt) survenant jusqu’au moment d’intérêt (c’est-à-dire cumulatif, à travers tous les temps avant le moment d’intérêt, voir l’exemple dans le tableau ci-dessous). Les erreurs standard sont calculées pour les estimations de survie pour les données du tableau ci-dessous. Notez que la dernière colonne indique la quantité 1,96*SE(St) qui est la marge d’erreur et qui est utilisée pour calculer les estimations de l’intervalle de confiance à 95% (c’est-à-dire St ± 1,96 x SE(St)).
Erreurs standard des estimations de survie
|
Temps, Années |
Nombre à risque Nt |
Nombre de décès Dt |
Survie. Probabilité St |
|
|
|
1.96*SE (St) |
|---|---|---|---|---|---|---|---|
|
0 |
20 |
|
1 |
|
. |
|
|
|
1 |
20 |
1 |
0.950 |
0.003 |
0.003 |
0.049 |
0.096 |
|
2 |
19 |
|
0.950 |
0.000 |
0.003 |
0.049 |
0.096 |
|
3 |
18 |
1 |
0.897 |
0.003 |
0.006 |
0.069 |
0.135 |
|
5 |
17 |
1 |
0.844 |
0.004 |
0.010 |
0.083 |
0.162 |
|
6 |
16 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
9 |
15 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
10 |
14 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
11 |
13 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
12 |
12 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
13 |
11 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
14 |
10 |
1 |
0.760 |
0.011 |
0.021 |
0.109 |
0.214 |
|
17 |
9 |
1 |
0.676 |
0.014 |
0.035 |
0.126 |
0.246 |
|
18 |
7 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
19 |
6 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
21 |
5 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
23 |
4 |
1 |
0.507 |
0.083 |
0.118 |
0.174 |
0.341 |
|
24 |
3 |
|
0.507 |
0,000 |
0,118 |
0,174 |
0,341 |
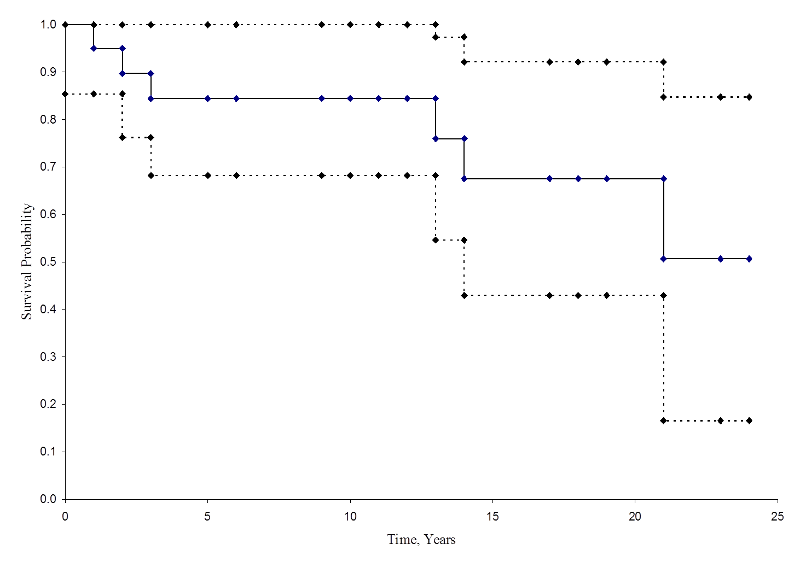
La figure ci-dessous résume les estimations et les intervalles de confiance. La courbe de survie de Kaplan-Meier est représentée par une ligne pleine, et les limites de confiance à 95 % sont représentées par des lignes pointillées.
Courbe de survie de Kaplan-Meier avec intervalles de confiance
Courbes d’incidence cumulative
Certains investigateurs préfèrent générer des courbes d’incidence cumulative, par opposition aux courbes de survie qui montrent les probabilités cumulatives de connaître l’événement d’intérêt. L’incidence cumulée, ou probabilité d’échec cumulée, est calculée comme 1-St et peut être calculée facilement à partir de la table de survie en utilisant l’approche de Kaplan-Meier. Les probabilités de défaillance cumulées pour l’exemple ci-dessus sont présentées dans le tableau ci-dessous.
Tableau de vie avec probabilités de défaillance cumulatives
|
Temps, Années |
Nombre à risque Nt |
Nombre de décès Dt |
Nombre. Censuré Ct |
Probabilité de survie St |
Probabilité d’échec 1-.St |
|---|---|---|---|---|---|
|
0 |
20 |
|
1 |
0 |
|
|
1 |
20 |
1 |
|
0.950 |
0.050 |
|
2 |
19 |
|
1 |
0.950 |
0.050 |
|
3 |
18 |
1 |
|
0.897 |
0.103 |
|
5 |
17 |
1 |
|
0.844 |
0.156 |
|
6 |
16 |
|
1 |
0.844 |
0.156 |
|
9 |
15 |
|
1 |
0.844 |
0.156 |
|
10 |
14 |
|
1 |
0.844 |
0.156 |
|
11 |
13 |
|
1 |
0.844 |
0.156 |
|
12 |
12 |
|
1 |
0.844 |
0.156 |
|
13 |
11 |
|
1 |
0.844 |
0.156 |
|
14 |
10 |
1 |
|
0.760 |
0.240 |
|
17 |
9 |
1 |
1 |
0.676 |
0.324 |
|
18 |
7 |
|
1 |
0.676 |
0.324 |
|
19 |
6 |
|
1 |
0.676 |
0.324 |
|
21 |
5 |
|
1 |
0.676 |
0.324 |
|
23 |
4 |
1 |
|
0.507 |
0.493 |
|
24 |
3 |
|
3 |
0.507 |
0,493 |
La figure ci-dessous montre l’incidence cumulative des décès pour les participants inscrits à l’étude décrite ci-dessus.
Courbe d’incidence cumulative
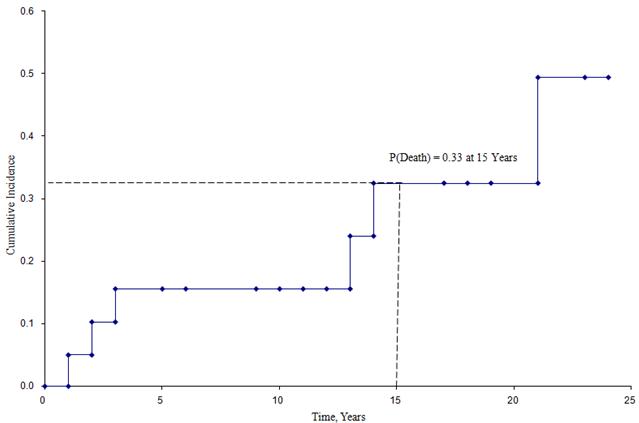
À partir de cette figure, nous pouvons estimer la probabilité qu’un participant décède à un certain moment. Par exemple, la probabilité de décès est d’environ 33 % à 15 ans (Voir les lignes pointillées).
retour en haut | page précédente | page suivante
.