6.3 Réseaux de croyance
La notion d’indépendance conditionnelle peut être utilisée pour donner une représentation concise de nombreux domaines. L’idée est que, étant donné une variable aléatoire X, il peut exister un petit ensemble de variables qui affectent directement la valeur de la variable dans le sens où X estconditionnellement indépendant des autres variables étant donné les valeurs des variables affectant directement. L’ensemble des variables affectant localement est appelé la couverture de Markov. C’est cette localité qui est exploitée dans un réseau de croyances. Un réseau de croyances est un modèle dirigé de dépendance conditionnelle entre un ensemble de variables aléatoires. L’énoncé précis de l’indépendance conditionnelle dans un réseau de croyance tient compte de la directionnalité.
Pour définir un réseau de croyance, commencez par un ensemble de variables aléatoires qui représentent toutes les caractéristiques du modèle. Supposons que ces variables sont {X1,…,Xn}.Ensuite, sélectionnez un ordonnancement total des variables, X1,…,Xn.
La règle de la chaîne (proposition 6.3) montre comment décomposer une conjonction en probabilités conditionnelles :
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Ou, en termes de variables aléatoires et de distributions de probabilité,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Définissez les parents de la variable aléatoire Xi, écritsparents(Xi), comme étant un ensemble minimal de prédécesseurs de Xi dans l’ordre total tel que les autres prédécesseurs de Xi sont conditionnellement indépendants de Xi étant donnéparents(Xi). C’est-à-dire, parents(Xi) ⊆{X1,…,Xi-1} tel que
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
Si plus d’un ensemble minimal existe, tout ensemble minimalpeut être choisi pour être les parents. Il ne peut y avoir plus d’un ensemble minimal que lorsque certains des prédécesseurs sont des fonctions déterministes des autres.
On peut mettre ensemble la règle de la chaîne et la définition des parents,donnant
P(X1, X2,—, Xn) = ∏i=1n P(Xi|parents(Xi)).
La probabilité sur l’ensemble des variables, P(X1, X2,—,Xn), est appelée distribution de probabilité conjointe. Un réseau de croyance définit une factorisation de la distribution de probabilité conjointe, où les probabilités conditionnelles forment des facteurs qui sont multipliés ensemble.
Un réseau de croyance, également appelé réseau bayésien, est un graphe dirigé acyclique (DAG), oùles nœuds sont des variables aléatoires. Il y a un arc de chaque élément deparents(Xi) dans Xi.Associé au réseau de croyance est un ensemble de distributions de probabilité conditionnelle – la probabilité conditionnelle de chaque variable étant donné ses parents (qui comprend les probabilités antérieures des variables sans parents).
Ainsi, un réseau de croyance se compose
- d’un DAG, où chaque nœud est étiqueté par une variable aléatoire;
- un domaine pour chaque variable aléatoire ; et
- un ensemble de distributions de probabilité conditionnelle donnant P(X|parents(X)) pour chaque variable X.
Un réseau de croyance est acyclique par construction. La façon dont la chaîne gouvernée décompose la conjonction donne l’ordre. Une variable ne peut avoir que des prédécesseurs comme parents.Différentes décompositions peuvent donner lieu à différents réseaux de croyance.
Supposons que nous utilisons les variables suivantes, toutes booléennes, dans l’ordre suivant :
- L’altération est vraie lorsqu’il y a altération de l’alarme.
- Feu est vrai lorsqu’il y a un incendie.
- Alarme est vrai lorsque l’alarme retentit.
- Fumée est vrai lorsqu’il y a de la fumée.
- Départ est vrai si de nombreuses personnes quittent le bâtiment en même temps.
- Rapport est vrai s’il y a un rapport donné par quelqu’un de personnes qui partent. Rapport est faux s’il n’y a pas de rapport de départ.
La variable Rapport désigne le rapport du capteur selon lequel les gens partent. Cette information n’est pas fiable car la personne qui émet un tel rapport peut être en train de faire une blague pratique, ou bien personne qui aurait pu donner un tel rapport peut avoir été attentif. Cette variable est introduite pour permettre le conditionnement sur des données de capteur non fiables. L’agent sait ce que le capteur rapporte, mais il ne dispose que de preuves non fiables sur les personnes qui quittent le bâtiment.Dans le cadre du domaine, supposez les indépendances conditionnelles suivantes :
- L’incendie est conditionnellement indépendant de l’altération (étant donné aucune autre information).
- L’alarme dépend à la fois de l’incendie et de l’altération. C’est-à-dire que nous ne faisons aucune hypothèse d’indépendance sur la façon dont l’alarme dépend de ses prédécesseurs étant donné cet ordre de variables.
- La fumée ne dépend que de l’incendie et est conditionnellement indépendante de l’altération et de l’alarme étant donné qu’il y a ou non un incendie.
- Le départ ne dépend que de l’alarme et pas directement de l’incendie ou de l’altération ou de la fumée. C’est-à-dire que le fait de partir est conditionnellement indépendant des autres variables étant donné l’alarme.
- Le rapport ne dépend directement que du fait de partir.
Le réseau de croyance de la figure 6.1 exprime ces dépendances.
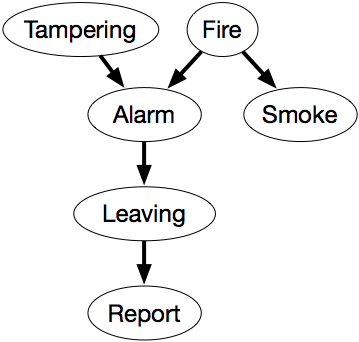
Ce réseau représente la factorisation
P(Falsification, incendie, alarme, fumée, départ,Rapport) = P(Falsification) ×P(Incendie) ×P(Alarme|Falsification,Incendie) ×P(Fumée|incendie) ×P(Départ|Alarme) ×P(Rapport|Départ).
Nous devons également définir le domaine de chaque variable. Supposons que lesvariables soient booléennes, c’est-à-dire qu’elles aient le domaine {vrai,faux}. Nous utilisons la variante en minuscule de la variable pour représenter la valeur vraie et utilisons la négation pour la valeur fausse. Ainsi, par exemple, Tampering=true s’écrit tampering, etTampering=false s’écrit ¬tampering.
Les exemples qui suivent supposent les probabilités conditionnelles suivantes :
P(incendie) = 0,01
P(alarme | incendie ∧tampering) = 0.5
P(alarme | feu ∧¬tampering) = 0.99
P(alarme | ¬feu ∧tampering) = 0.85
P(alarme | ¬feu ∧¬tampering) = 0.0001
P(fumée | feu ) = 0.9
P(fumée | ¬incendie ) = 0.01
P(sortie | alarme) = 0.88
P(sortie | ¬alarme ) = 0.001
P(rapport | sortie ) = 0.75
P(rapport | ¬sortie ) = 0.01
- Pour chaque fil wi, il existe une variable aléatoire, Wi, de domaine {live,dead}, qui indique s’il y a du courant dans le fil wi. Wi=live signifie que le filwi est alimenté. Wi=dead signifie qu’il n’y a pas de puissance dans le fil wi.
- Puissance_extérieure avec le domaine {live,dead} dénote s’il y a de la puissance qui entre dans le bâtiment.
- Pour chaque interrupteur si, la variable Si_pos dénote la position desi. Elle a pour domaine {haut,bas}.
- Pour chaque commutateur si, la variable Si_st dénote l’état du commutateur si. Elle a pour domaine {ok,upside_down,short,intermittent,broken}. Si_st=ok signifie que le commutateur si fonctionne normalement. Si_st=upside_down signifie que le commutateur si est installé à l’envers. Si_st=court signifie que le commutateur si est court-circuité et agit comme un fil. Si_st=broken signifie que l’interrupteur si est cassé et ne permet pas à l’électricité de circuler.
- Pour chaque disjoncteurercbi, la variable Cbi_st a pour domaine {on,off}. Cbi_st=on signifie que le courant peut circuler à travers cbi et Cbi_st=off signifie que le courant ne peut pas circuler à travers cbi.
- Pour chaque lumière li, la variable Li_st avec le domaine {ok,intermittent,cassé} dénote l’état de la lumière. Li_st=ok signifie que la lumière li s’allumera si elle est alimentée, Li_st=intermittent signifie que la lumière li s’allume par intermittence si elle est alimentée, et Li_st=broken signifie que la lumière li ne fonctionne pas.
Choisissons un ordre où les causes d’une variable sont avant la variable dans l’ordre. Par exemple, la variable permettant de savoir si une lumière est allumée vient après les variables permettant de savoir si la lumière fonctionne et s’il y a du courant qui arrive dans la lumière.
Le fait que la lumière l1 soit allumée dépend uniquement du fait qu’il y ait du courant dans le fil w0 et que la lumière l1 fonctionne correctement. D’autres variables, comme la position de l’interrupteur s1, si la lumière l2 est allumée ou qui est la reine du Canada, ne sont pas pertinentes. Ainsi, les parents de L1_lit sont W0 et L1_st.
Considérez la variable W0, qui représente s’il y a du courant dans le fil w0. Si nous savions s’il y a du courant dans les fils w1 etw2, et si nous connaissions la position de l’interrupteur s2 et si l’interrupteur fonctionnait correctement, la valeur des autres variables (autres queL1_lit) n’affecterait pas notre croyance en la présence de courant dans le fil w0. Ainsi, les parents de W0 devraient être S2_Pos, S2_st,W1, et W2.
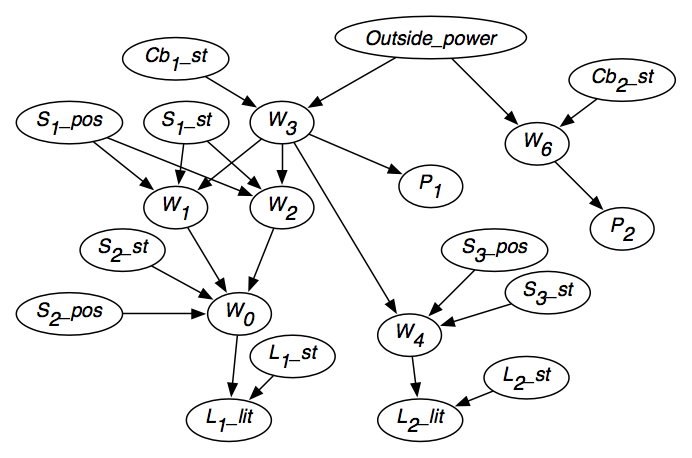
La figure 6.2 montre le réseau de croyance résultant après que l’indépendance de chaque variable ait été prise en compte.Le réseau de croyance contient également les domaines des variables, tels qu’indiqués dans la figure, et les probabilités conditionnelles de chaque variable étant donné ses parents.
Pour la variable W1, les probabilités conditionnelles suivantes doivent être spécifiées :
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=live|S1_pos=down ∧S1_st=broken ∧W3=dead).
Il y a deux valeurs pour S1_pos, cinq valeurs pour S1_ok, etdeux valeurs pour W3, donc il y a 2×5 ×2 = 20 cas différents où une valeur pour W1=live doit être spécifiée. En ce qui concerne la théorie de la probabilité, la probabilité pour W1=live dans ces 20 cas pourrait être attribuée arbitrairement. Bien sûr, la connaissance du domaine limite les valeurs qui ont un sens. Les valeurs de W1=mort peuvent être calculées à partir des valeurs de W1=vivant pour chacun de ces cas.
Parce que la variable S1_st n’a pas de parents, elle nécessite une distribution antérieure, qui peut être spécifiée comme les probabilités pour toutes les valeurs sauf une ; la valeur restante peut être dérivée de la contrainte que la somme de toutes les probabilités soit égale à 1. Ainsi, pour spécifier la distribution de S1_st, quatre des cinq probabilités suivantes doivent être spécifiées :
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Un réseau de croyance est une représentation graphique de l’indépendance conditionnelle.L’indépendance nous permet de représenter les effets directs dans le grapheet prescrit quelles probabilités doivent être spécifiées. Des probabilités postérieures arbitraires peuvent être dérivées du réseau.
L’hypothèse d’indépendance intégrée dans un réseau de croyance est la suivante :Chaque variable aléatoire est conditionnellement indépendante de ses non-descendants étant donné sesparents. C’est-à-dire, si X est une variable aléatoire avec des parents Y1,…, Yn, toutes les variables aléatoires qui ne sont pas des descendants deX sont conditionnellement indépendantes de X étant donné Y1,…, Yn :
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
si R n’implique pas un descendant de X. Pour cette définition, nousincluons X comme descendant de lui-même. Le côté droit de cette équation est la forme des probabilités qui sont spécifiées dans le cadre du réseau de croyance.R peut impliquer des ancêtres de X et d’autres nœuds tant qu’ils ne sont pas descendants de X. L’hypothèse d’indépendance stipule que toute l’influence des variables non descendantes est capturée en connaissant la valeur des parents de X.
Souvent, nous nous référons juste au DAG étiqueté comme un réseau de croyance. Lorsque cela est fait, il est important de se rappeler qu’un domaine pour chaque variable et un ensemble de distributions de probabilités conditionnelles font également partie du réseau.
Le nombre de probabilités qui doivent être spécifiées pour chaque variable est exponentiel dans le nombre de parents de la variable.
L’hypothèse d’indépendance est utile dans la mesure où le nombre de variables qui affectent directement une autre variable est faible. Vous devriez ordonner les variables de façon à ce que les nœuds aient le moins de parents possible.
Réseaux de croyance et causalité
Les réseaux de croyance ont souvent été appelés réseaux de causalité et on a prétendu qu’ils représentaient bien la causalité.Rappelez-vous qu’un modèle de causalité prédit le résultat des interventions.Supposons que vous ayez en tête un modèle de causalité d’un domaine, où le domaine est spécifié en termes d’un ensemble de variables aléatoires. Pour chaque paire de variables aléatoires X1et X2, s’il existe un lien causal direct entre X1 et X2 (c’est-à-dire que l’intervention pour modifier X1 dans un certain contexte d’autres variables affecte X2 et que cela ne peut pas être modélisé par une variable d’intervention), ajoutez un arc deX1 à X2. On peut s’attendre à ce que le modèle causal obéisse à l’hypothèse d’indépendance du réseau de croyances. Ainsi, toutes les conclusions du réseau de croyances seraient valides.
Vous vous attendriez également à ce qu’un tel graphe soit acyclique ; vous ne voulez pas que quelque chose finisse par se causer lui-même. Cette hypothèse est raisonnable si vousconsidérez que les variables aléatoires représentent des événements particuliers plutôt que des types d’événements. Par exemple, considérons une chaîne causale selon laquelle “être stressé” vous amène à “travailler de manière inefficace”, ce qui, à son tour, vous amène à “être stressé”. Pour briser le cycle apparent, nous pouvons représenter “être stressé” à différents stades comme des variables aléatoires différentes qui se réfèrent à des moments différents. Le fait d’être stressé dans le passé fait que vous ne travaillez pas bien en ce moment, ce qui vous rendra stressé à l’avenir. Les variables doivent satisfaire au principe de clarté et avoir une signification bien définie. Les variables ne doivent pas être considérées comme des types d’événements.
Le réseau de croyances lui-même n’a rien à dire sur la causalité, et il peut représenter une indépendance non causale, mais il semble particulièrement approprié lorsqu’il y a une causalité dans un domaine. L’ajout d’arcs qui représentent la causalité locale tend à produire un petit réseau de croyance. Le réseau de croyance de laFigure 6.2 montre comment cela peut être fait pour un domaine simple.
Un réseau causal modélise les interventions. Si quelqu’un devait forcer artificiellement une variable à avoir une valeur particulière, les descendants de la variable – mais aucun autre nœud – seraient affectés. Enfin, vous pouvez voir comment la causalité des réseaux de croyances est liée au raisonnement causal et probatoire abordé à la section 5.7. Un réseau de croyances causal peut être considéré comme une axiomatisation dans une direction causale. Le raisonnement dans les réseaux de croyances correspond à la déduction des causes et à la prédiction à partir de celles-ci. Il existe une correspondance directe entre le point de vue abductif basé sur la logique abordé dans la section 5.7 et les réseaux de croyances : Les réseaux de croyances peuvent être modélisés comme des programmes logiques avec des probabilités sur les hypothèses possibles. Ceci est décrit dans la section 14.3.
Notez la restriction “chaque variable aléatoire est conditionnellement indépendante de ses non-descendants étant donné sesparents” dans la définition de l’indépendanceencodée dans un réseau de croyances. SiR contient un descendant de la variable X, l’hypothèse d’indépendance n’est pas directement applicable.
La variable S1_pos n’a pas de parents. Ainsi, l’indépendance intégrée dans le réseau de croyances spécifie que P(S1_pos=up|A) =P(S1_pos=up) pour tout A qui n’implique pas un descendant deS1_pos. Si A comprend un descendant de S1_pos=up – par exemple,si A est S2_pos=up∧L1_lit=vrai – l’hypothèse d’indépendance ne peut pas être directement appliquée.
Ce réseau peut être utilisé de plusieurs façons :
- En conditionnant sur la connaissance que les interrupteurs et les disjoncteurs sont ok, et sur les valeurs de la puissance extérieure et la position des interrupteurs, ce réseau peut simuler comment l’éclairage devrait fonctionner.
- Sous réserve des valeurs de la puissance extérieure et de la position des interrupteurs, le réseau peut déduire la probabilité de tout résultat – par exemple, la probabilité que l1 soit allumée.
- Donné les valeurs des interrupteurs et si les lumières sont allumées,la probabilité postérieure que chaque interrupteur ou disjoncteur soit dans n’importe quel état particulier peut être déduite.
- Donné certaines observations, le réseau peut être utilisé pour raisonner en arrière afin de déterminer la position la plus probable des interrupteurs.
- Sous réserve de certaines positions de commutateurs, de certaines sorties et de certaines valeurs intermédiaires, le réseau peut être utilisé pour déterminer la probabilité de toute autre variable du réseau.
Un réseau de croyance spécifie une distribution de probabilité conjointe à partir de laquelle des probabilités conditionnelles arbitraires peuvent être dérivées. Un réseau peut être interrogé en demandant la probabilité conditionnelle de n’importe quelles variables conditionnées par les valeurs de n’importe quelles autres variables. Ceci est typiquement fait en fournissant des observations sur certaines variables et en interrogeant une autre variable.
P(feu) = 0,01
P(rapport ) = 0,028
P(fumée) = 0.0189
L’observation du rapport donne ce qui suit :
P(feu |rapport)= 0,2305
P(fumée |rapport) = 0,215
Comme prévu, la probabilité de falsification et d’incendie est augmentée par le rapport. Comme le feu est augmenté, la probabilité de la fumée l’est aussi.
Supposons plutôt que de la fumée ait été observée :
P(incendie|fumée) = 0,476
P(rapport |fumée) = 0,320
Notez que la probabilité d’altération n’est pas affectée par l’observation de la fumée ; cependant, les probabilités de rapport et d’incendie sont augmentées.
Supposons que le signalement et la fumée aient tous deux été observés :
P(incendie |signalement ∧smoke) = 0,964
L’observation des deux rend l’incendie encore plus probable. Cependant, dans le contexte du rapport, la présence de fumée rend la falsification moins probable. Cela est dû au fait que le rapport est expliqué par le feu, qui est maintenant plus probable.
Supposons plutôt que le rapport, mais pas la fumée, a été observé :
P(feu|rapport ∧¬fumée) = 0,0294
Dans le contexte du rapport, le feu devient beaucoup moins probable et sla probabilité de falsification augmente pour expliquer le rapport.
Cet exemple illustre comment l’hypothèse d’indépendance du réseau de croyances donne des conclusions de bon sens et démontre également comment l’explication est une aconsequence de l’hypothèse d’indépendance d’un réseau de croyances.
- 6.3.1 Construction de réseaux de croyances
.