Le flux StatsTest : Prédiction >> Variable dépendante continue >> Plus d’une variable indépendante >> Pas de mesures répétées >> Une variable dépendante

Vous n’êtes pas sûr qu’il s’agisse de la bonne méthode statistique ? Utilisez le flux de travail Choisissez votre test statistique pour sélectionner la bonne méthode.

Qu’est-ce que la régression linéaire multiple multivariée ?

La régression linéaire multiple multivariée est un test statistique utilisé pour prédire plusieurs variables de résultat à l’aide d’une ou plusieurs autres variables. Il est également utilisé pour déterminer la relation numérique entre ces ensembles de variables et d’autres. La variable que vous voulez prédire doit être continue et vos données doivent satisfaire aux autres hypothèses énumérées ci-dessous.

Assomptions pour la régression linéaire multiple multivariée

Toute méthode statistique comporte des hypothèses. Les hypothèses signifient que vos données doivent satisfaire certaines propriétés pour que les résultats des méthodes statistiques soient exacts.

Les hypothèses pour la régression linéaire multiple multivariée comprennent :

1. Linéarité
2. Pas de valeurs aberrantes
3. Etendue similaire sur la plage
4. Normalité des résidus
5. Pas de multicolinéarité

Plongeons chacune d’entre elles séparément.

Linéarité

Les variables qui vous intéressent doivent être liées linéairement. Cela signifie que si vous tracez les variables, vous serez en mesure de tracer une ligne droite qui correspond à la forme des données.

Pas de valeurs aberrantes

Les variables qui vous intéressent ne doivent pas contenir de valeurs aberrantes. La régression linéaire est sensible aux valeurs aberrantes, ou aux points de données qui ont des valeurs inhabituellement grandes ou petites. Vous pouvez dire si vos variables ont des valeurs aberrantes en les traçant et en observant si des points sont éloignés de tous les autres points.

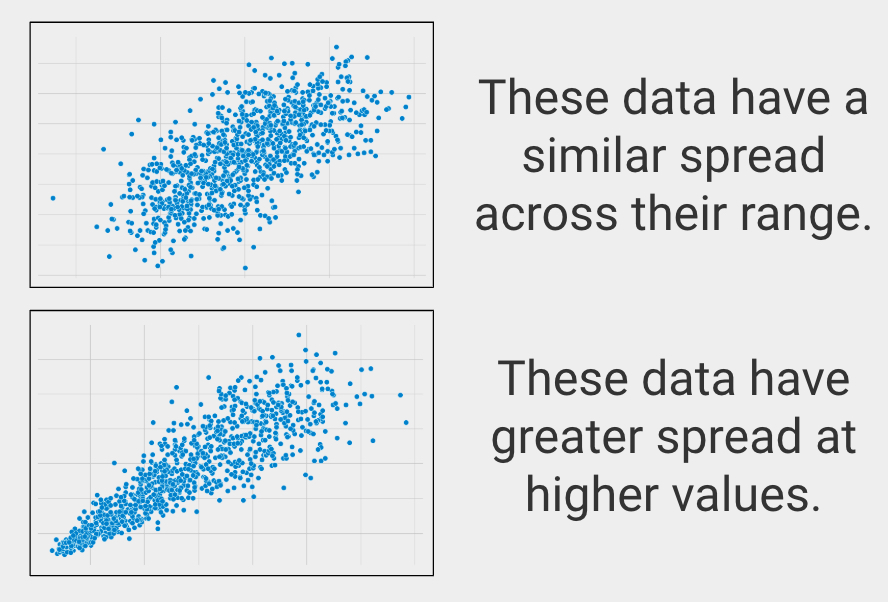
Dispersion similaire sur l’étendue

En statistique, on appelle cela l’homoscédasticité, qui décrit quand les variables ont une dispersion similaire sur leur étendue.

Normalité des résidus

Le mot “résidus” désigne les valeurs résultant de la soustraction des variables dépendantes attendues (ou prédites) des valeurs réelles. La distribution de ces valeurs doit correspondre à une forme de distribution normale (ou courbe en cloche).

Répondre à cette hypothèse assure que les résultats de la régression sont également applicables sur toute la dispersion des données et qu’il n’y a pas de biais systématique dans la prédiction.

Pas de multicollinéarité

La multicollinéarité fait référence au scénario où deux ou plusieurs des variables indépendantes sont substantiellement corrélées entre elles. Lorsque la multicollinéarité est présente, les coefficients de régression et la signification statistique deviennent instables et moins dignes de confiance, bien que cela n’affecte pas la façon dont le modèle s’adapte aux données en soi.

Quand utiliser la régression linéaire multiple multivariée ?

Vous devriez utiliser la régression linéaire multiple multivariée dans le scénario suivant :

1. Vous voulez utiliser une variable dans une prédiction de plusieurs autres variables, ou vous voulez quantifier la relation numérique entre elles
2. Les variables que vous voulez prédire (votre variable dépendante) sont continues
3. Vous avez plus d’une variable indépendante, ou une variable que vous utilisez comme prédicteur
4. Vous n’avez pas de mesures répétées de la même unité d’observation
5. Vous avez plus d’une variable dépendante

Détaillons-les pour vous aider à savoir quand utiliser la régression linéaire multiple multivariée.

Prédiction

Vous cherchez un test statistique pour prédire une variable à l’aide d’une autre. Il s’agit d’une question de prédiction. D’autres types d’analyses consistent à examiner la force de la relation entre deux variables (corrélation) ou à examiner les différences entre les groupes (différence).

Variable dépendante continue

La variable que vous voulez prédire doit être continue. Continue signifie que votre variable d’intérêt peut fondamentalement prendre n’importe quelle valeur, comme la fréquence cardiaque, la taille, le poids, le nombre de barres de crème glacée que vous pouvez manger en 1 minute, etc.

Les types de données qui ne sont PAS continues comprennent les données ordonnées (comme la place d’arrivée dans une course, le classement des meilleures entreprises, etc.), les données catégorielles (sexe, couleur des yeux, race, etc.) ou les données binaires (a acheté le produit ou non, est atteint de la maladie ou non, etc.)

Si votre variable dépendante est binaire, vous devez utiliser la régression logistique multiple, et si votre variable dépendante est catégorique, alors vous devez utiliser la régression logistique multinomiale ou l’analyse discriminante linéaire.

Plus d’une variable indépendante

La régression linéaire multiple multivariée est utilisée lorsqu’il y a une ou plusieurs variables prédictives avec plusieurs valeurs pour chaque unité d’observation.

Pas de mesures répétées

Cette méthode est adaptée au scénario où il n’y a qu’une seule observation pour chaque unité d’observation. L’unité d’observation est ce qui compose un “point de données”, par exemple, un magasin, un client, une ville, etc…

Si vous avez une ou plusieurs variables indépendantes mais qu’elles sont mesurées pour le même groupe à plusieurs moments, alors vous devez utiliser un modèle à effets mixtes.

Plus d’une variable dépendante

Pour exécuter une régression linéaire multiple multivariée, vous devez avoir plus d’une variable dépendante, ou variable que vous essayez de prédire.

Si vous ne prédisez qu’une variable, vous devez utiliser la régression linéaire multiple.

Régression linéaire multiple multivariée Exemple

Variable dépendante 1 : Recettes
Variable dépendante 2 : Trafic de clients
Variable indépendante 1 : Dollars dépensés en publicité par ville
Variable indépendante 2 : Population de la ville

L’hypothèse nulle, qui est le jargon statistique pour dire ce qui se passerait si le traitement ne fait rien, est qu’il n’y a pas de relation entre les dépenses en publicité et les dollars publicitaires ou la population par ville. Notre test évaluera la probabilité que cette hypothèse soit vraie.

Nous rassemblons nos données et après nous être assurés que les hypothèses de la régression linéaire sont respectées, nous effectuons l’analyse.

Cette analyse exécute effectivement une régression linéaire multiple deux fois en utilisant les deux variables dépendantes. Ainsi, lorsque nous exécutons cette analyse, nous obtenons des coefficients bêta et des valeurs p pour chaque terme du modèle “revenu” et du modèle “trafic client”. Pour tout modèle de régression linéaire, vous aurez un coefficient bêta égal à l’ordonnée à l’origine de votre ligne de régression linéaire (souvent marquée d’un 0 comme β0). Il s’agit simplement de l’endroit où la ligne de régression croise l’axe des y si vous deviez tracer vos données. Dans le cas d’une régression linéaire multiple, il y a en plus deux autres coefficients bêta (β1, β2, etc), qui représentent la relation entre les variables indépendantes et dépendantes.

Ces coefficients bêta supplémentaires sont la clé pour comprendre la relation numérique entre vos variables. Essentiellement, pour chaque unité (valeur de 1) d’augmentation d’une variable indépendante donnée, votre variable dépendante devrait changer de la valeur du coefficient bêta associé à cette variable indépendante (tout en maintenant les autres variables indépendantes constantes).

La valeur p associée à ces valeurs bêta supplémentaires est la chance de voir nos résultats en supposant qu’il n’y a en fait aucune relation entre cette variable et le revenu. Une valeur p inférieure ou égale à 0,05 signifie que notre résultat est statistiquement significatif et que nous pouvons croire que la différence n’est pas due au seul hasard. Pour obtenir une valeur p globale pour le modèle et des valeurs p individuelles qui représentent les effets des variables entre les deux modèles, on utilise souvent des MANOVA.

De plus, cette analyse donnera lieu à une valeur R-Squared (R2). Cette valeur peut varier de 0 à 1 et représente la façon dont votre ligne de régression linéaire s’adapte à vos points de données. Plus le R2 est élevé, mieux votre modèle s’adapte à vos données.

Frequently Asked Questions

Q : Quelle est la différence entre la régression linéaire multiple multivariée et l’exécution de la régression linéaire plusieurs fois ?
A : Ils sont conceptuellement similaires, car les coefficients individuels du modèle seront les mêmes dans les deux scénarios. Une différence substantielle, cependant, est que les tests de signification et les intervalles de confiance pour la régression linéaire multivariée tiennent compte des multiples variables dépendantes.

Q : Comment puis-je exécuter la régression linéaire multiple multivariée dans SPSS, R, SAS ou STATA?
A : Cette ressource vise à vous aider à choisir la bonne méthode statistique à chaque fois. Il existe de nombreuses ressources disponibles pour vous aider à comprendre comment exécuter cette méthode avec vos données :
R article : https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/

Aide!

Si vous n’arrivez toujours pas à comprendre quelque chose, n’hésitez pas à nous contacter.