Tétraèdre

Contenu de la page Qu’est-ce qu’un tétraèdre ? Pièces du tétraèdre Nombres tétraédriques Tétraèdre dans leCube Anneaux de tétraèdres Tétraèdres sur l’Internet

A la page principale “Mathematische Basteleien”

Qu’est-ce qu’un tétraèdre ?

Un tétraèdre est une figure à trois dimensions comportant quatre triangles équilatéraux. Si vous soulevez trois triangles (1), vous obtenez le tétraèdreen vue de dessus (2). Généralement, il est représenté en perspective (3).

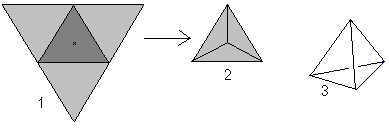
Si l’on considère le mot tétraèdre (tétraèdre signifie “à quatre plans”), on pourrait appeler tétraèdre toute pyramide dont la base est un triangle.

Cependant, le tétraèdre est la pyramide triangulaire droite et régulière de ce site.

Pièces duTétraèdre
Hauteur et aire d’un triangle latéral
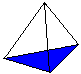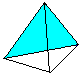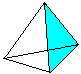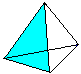
Quatre triangles équilatéraux forment un tétraèdre.

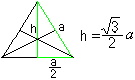…	Un triangle est choisi : Les trois hauteurs se coupent en un point comme dans tout triangle. C’est le centre du triangle. La hauteur peut être calculée par le côté a comme h=sqr(3)/2*a en utilisant le théorème de Pythagore.

Les hauteurs sont aussi des médianes et se coupent avec le rapport2:1. Cela est utilisé dans les calculs suivants.

L’aire du triangle est A=sqr(3)/4*a².

Hauteur de l’espace

La hauteur du tétraèdre est comprise entre le centre du triangle de base (1) et le sommet (2). Pour les calculs, on considère ce qu’on appelle le triangle d’appui (3, jaune), qui est formé par une arête et deux hauteurs de triangle. On a H=sqr(6)/3*a en utilisant le théorème de Pythagore.
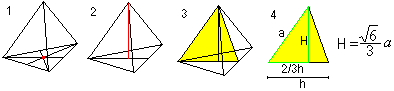
Centre, sphère circonscrite et sphère inscrite Le centre d’un tétraèdre est l’intersection de deux hauteurs d’espace (1,2,3). C’est le centre de gravité, le centre de la sphère par les quatre coins, et le centre de la plus grande sphère, qui tient encore à l’intérieur du tétraèdre (4).

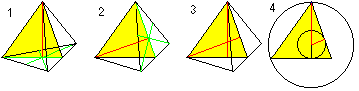
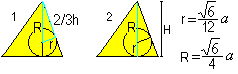….	On obtient deux formules pour r et R à l’aide du théorème de Pythagore (1) et de H=R+r (2): On a r=sqr(6)/12*a , R=sqr(6)/4*a.

Surface de l’angle

….…..

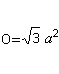L’aire de la base et des faces latérales forment la surfaceO. On a O=4*A (triangle) = sqr(3)a².

Volume

Nombres tétraédriques sommet

…….	Si vous collez 20 billes à deux groupes avec quatre et deux avec six, vous obtenez une énigme bien connue : vous devez former une pyramide avec quatre pièces.

Il existe de nombreuses énigmes similaires.

Tétraèdre dans le Cube haut
Six diagonales de face forment un tétraèdre dans le cube.
Si vous connaissez la vue 3D, vous pouvez regarder en trois dimensions les deux paires de cubes suivantes.

Le volume du tétraèdre est la troisième partie du volume du cube.

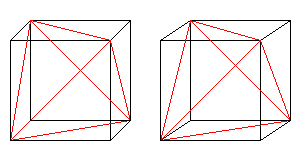
Si vous dessinez un deuxième tétraèdre et les lignes d’intersection,vous obtenez une pénétration de deux tétraèdres.

La figure est constituée des diagonales des faces et des lignes de liaison des centres des carrés latéraux du cube original. Les derniers forment un octaèdre.

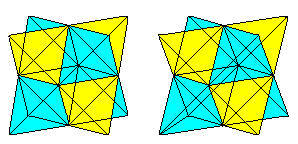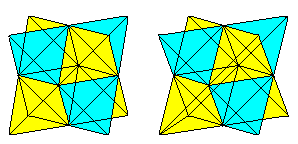
Anneaux de tétraèdres haut
Vous pouvez fabriquer des tétraèdres en papier et en coller un nombre pair sur un anneau. L’anneau peut continuellement se tordre vers l’intérieur ou l’extérieur par le centre. C’est un joli jouet. – Ces anneaux sont aussi appelés kaléidocycles.Vous en trouverez plus sur ma page web Kaleidocycles.

Tétraèdres sur le sommet de l’Internet

Allemand

Christof Weber
Washat dieser Körper mit Kugeln zu tun ? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

Anglais

Eric W. Weisstein (World of Mathematics)
Tétraèdre

H.B.Meyer (Polyeder aus Flechtstreifen)
Tétraèdre

Joyce Frost and Peg Cagle (mathforum)
AnAmazing, Space Filling, Non-regular Tetrahedron

Wikipedia
Tétraèdre,Tetrapode(structure), Tetrahedralnumber

.