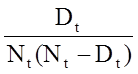Túlélési függvény vagy túlélési görbe becslésének többféle módja van. Számos népszerű parametrikus módszer létezik a túlélési adatok modellezésére, és ezek abban különböznek, hogy milyen feltételezéseket tesznek a túlélési idők eloszlásáról a populációban. Néhány népszerű eloszlás az exponenciális, a Weibull-, a Gompertz- és a log-normális eloszlás.2 Talán a legnépszerűbb az exponenciális eloszlás, amely feltételezi, hogy a résztvevő valószínűsége, hogy elszenvedi az adott eseményt, független attól, hogy az adott személy mennyi ideig volt eseménymentes. Más eloszlások különböző feltételezéseket tesznek az egyén esemény kialakulásának valószínűségére vonatkozóan (azaz az idővel növekedhet, csökkenhet vagy változhat). A túlélési elemzés parametrikus módszereiről részletesebben a Hosmer és Lemeshow és Lee és Wang1,3 könyvekben olvashatunk.

Ezekben két nemparametrikus módszerrel foglalkozunk, amelyek nem tesznek feltevéseket arra vonatkozóan, hogy az adott személynél hogyan változik az esemény bekövetkezésének valószínűsége az idő múlásával. A nemparametrikus módszerek segítségével megbecsüljük és ábrázoljuk a túlélési eloszlást vagy a túlélési görbét. A túlélési görbéket gyakran lépésfüggvényként ábrázolják, ahogy az alábbi ábrán látható. Az X tengelyen az idő, az Y tengelyen pedig a túlélés (a veszélyeztetett személyek aránya) látható. Megjegyzendő, hogy a túlélő résztvevők százalékos aránya nem mindig jelenti az életben lévők százalékos arányát (ami feltételezi, hogy az érdeklődésre számot tartó kimenetel a halál). A “túlélés” utalhat arra az arányra is, amelyik mentes egy másik kimenetelű eseménytől (pl. az MI vagy szív- és érrendszeri betegségtől mentes százalékos arány), vagy jelentheti azt a százalékos arányt is, amelyik nem éli meg az egészséges kimenetet (pl. a rák remissziója).

Túlélési függvény

Megfigyelhető, hogy a túlélés valószínűsége 2 évig 100%, majd 90%-ra csökken. A medián túlélés 9 év (azaz a populáció 50%-a éli túl a 9 évet; lásd a szaggatott vonalakat).

Példa:

Gondoljunk egy kis prospektív kohorszvizsgálatra, amelynek célja a halálozásig eltelt idő vizsgálata. A vizsgálatban 20 65 éves vagy annál idősebb résztvevő vesz részt; őket 5 éven keresztül veszik fel, és 24 évig követik őket, amíg meg nem halnak, a vizsgálat véget nem ér, vagy ki nem esnek a vizsgálatból (lost to follow-up). Az adatokat az alábbiakban mutatjuk be. A vizsgálatban 6 haláleset és 3 olyan résztvevő van, akinek teljes a követése (azaz 24 év). A fennmaradó 11 résztvevő 24 évnél rövidebb követési idővel rendelkezik, mivel későn jelentkeztek vagy elvesztették a követést.

A résztvevő azonosítószáma	A halál éve	Év Utolsó kapcsolatfelvétel éve
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

Élettáblázat (biztosításmatematikai táblázat)

A résztvevők tapasztalatainak összegzésének egyik módja az élettáblázat, vagy biztosításmatematikai táblázat segítségével. Az élettáblákat gyakran használják a biztosítási iparban a várható élettartam becslésére és a biztosítási díjak megállapítására. Mi a biostatisztikai elemzésekben széles körben használt élettáblázat egy speciális típusára, az úgynevezett kohorsz-élettáblázatra vagy követési élettáblázatra összpontosítunk. A követési élettábla összefoglalja a résztvevők tapasztalatait egy előre meghatározott követési időszak alatt egy kohorszvizsgálatban vagy egy klinikai vizsgálatban az érdeklődésre számot tartó esemény időpontjáig vagy a vizsgálat végéig, attól függően, hogy melyik következik be előbb.

Az élettábla elkészítéséhez először a követési időket egyenletes időközökbe rendezzük. A fenti táblázatban a maximális követési idő 24 év, és 5 éves intervallumokat veszünk figyelembe (0-4, 5-9, 10-14, 15-19 és 20-24 év). Összesítjük az egyes intervallumok kezdetén élő résztvevők számát, a halálesetek számát és a cenzorok számát az egyes intervallumokban.

Intervallum években	Az intervallum kezdetén élők száma	Az intervallum alatt meghaltak száma	A cenzúrázottak száma
0-4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

Élettábla-elemzésünkben a következő jelölést használjuk. Először definiáljuk a jelölést, majd ezt használjuk az élettábla felépítéséhez.

• Nt = azon résztvevők száma, akik a t intervallum alatt eseménymentesnek és kockázatosnak tekinthetők (pl., ebben a példában az élők száma, mivel a számunkra érdekes kimenetel a halál)
• Dt = azon résztvevők száma, akik a t intervallum alatt meghalnak (vagy elszenvedik az érdekes eseményt)
• Ct = azon résztvevők száma, akiket a t intervallum alatt cenzúráznak Nt* = a t intervallum alatt veszélyeztetett résztvevők átlagos száma
• Nt* = a t intervallum alatt veszélyeztetett résztvevők átlagos száma [A biztosításmatematikai élettáblák készítésekor gyakran a következő feltevéseket teszik: Először is, feltételezik, hogy az érdekes események (pl. halálozások) az intervallum végén következnek be, és feltételezik, hogy a cenzúrázott események egyenletesen (vagy egyenletesen) következnek be az intervallumban. Ezért gyakran kiigazítják az Nt-t, hogy tükrözze az intervallum alatt veszélyeztetett résztvevők átlagos számát, az Nt*-t, amelyet a következőképpen számítanak ki: Nt* =Nt-Ct/2 (azaz, a cenzúrázott események felét kivonjuk).
• qt = a t intervallum alatt meghalók (vagy eseményt elszenvedők) aránya, qt = Dt/Nt*
• pt = a t intervallumot túlélők (eseménymentesen maradó) aránya, pt = 1-qt
• St, a t intervallum után túlélők (vagy eseménymentesen maradó) aránya; ezt néha kumulatív túlélési valószínűségnek nevezik, és a következőképpen számítják: Először is, a 0. időpont (a kiindulási időpont) után túlélő résztvevők aránya S0 = 1 (minden résztvevő életben van vagy eseménymentes a nulladik időpontban vagy a vizsgálat kezdetén). Az egyes további intervallumokat túlélők arányát a feltételes valószínűségnek a Valószínűség modulban bemutatott elvei alapján számítjuk ki. Konkrétan, annak valószínűsége, hogy egy résztvevő túléli az 1. intervallumot, S1 = p1. Annak valószínűsége, hogy egy résztvevő túléli a 2. intervallumot, azt jelenti, hogy túl kellett élnie az 1. intervallumot és a 2. intervallumot: S2 = P(túlélni a 2. intervallumot) = P(túlélni a 2. intervallumot)*P(túlélni az 1. intervallumot), vagy S2 = p2*S1. Általában St+1 = pt+1*St.

A követési élettartam táblázat formátuma az alábbiakban látható.

Az első intervallumra, 0-4 évre: A 0. időpontban, az első intervallum (0-4 év) kezdetén 20 résztvevő él vagy van veszélyeztetve. Két résztvevő meghal az intervallumban, 1 pedig cenzúrázásra kerül. Alkalmazzuk az adott intervallumban cenzúrázott résztvevők számának korrekcióját, így Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. A többi oszlop számításait a táblázat mutatja. Annak valószínűsége, hogy egy résztvevő túléli a 4 évet, vagyis az első intervallumot (az intervallum felső határát használva az idő meghatározására), S4 = p4 = 0,897.

A második intervallumra, 5-9 évre: A veszélyeztetett szám az előző intervallumban (0-4 év) veszélyeztetett szám, csökkentve azokkal, akik meghalnak és cenzúrázásra kerülnek (azaz Nt = Nt-1-Dt-1-Dt-1-Ct-1 = 20-2-1 = 17). Annak valószínűsége, hogy egy résztvevő 9 évnél tovább él, S9 = p9*S4 = 0,937*0,897 = 0,840.

Intervallum években	Veszélyeztetett személyek száma az intervallum alatt, Nt	Az átlagos veszélyeztetett személyek száma az intervallum alatt, Nt*	A halálesetek száma az intervallum alatt, Dt	Követési időre elveszett, Ct	Halálozás aránya az intervallum alatt, qt	Among those at risk, Proportion Surviving Interval, pt	Túlélési valószínűség St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

A teljes követési élettartam táblázat az alábbiakban látható.

Intervallum években	Rizikószám az intervallum alatt, Nt	Az átlagszám az intervallum alatt, Nt*	A halálesetek száma az intervallum alatt, Dt	Követési időre elveszett, Ct	Halálozás aránya az intervallum alatt, qt	A veszélyeztetettek körében, Proportion Surviving Interval,pt	Survival Probability St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Ez a táblázat a biztosításmatematikai módszert használja az utóéletkor táblázatának elkészítéséhez, ahol az időt egyenlő időközökre osztjuk.

Kaplan-Meier (Product Limit) megközelítés

A fent bemutatott élettábla megközelítéssel kapcsolatban az a probléma, hogy a túlélési valószínűségek változhatnak az intervallumok szervezésének függvényében, különösen kis minták esetén. A Kaplan-Meier-megközelítés, más néven termékhatár-megközelítés egy népszerű megközelítés, amely ezt a problémát úgy kezeli, hogy a túlélési valószínűséget minden egyes esemény bekövetkezésekor újrabecsüli.

A Kaplan-Meier-megközelítés megfelelő alkalmazása azon a feltételezésen alapul, hogy a cenzúra független az érdekes esemény kialakulásának valószínűségétől, és hogy a túlélési valószínűségek összehasonlíthatóak a vizsgálatba korán és később felvett résztvevők esetében. Több csoport összehasonlításakor az is fontos, hogy ezek a feltételezések minden egyes összehasonlító csoportban teljesüljenek, és például a cenzúra ne legyen valószínűbb az egyik csoportban, mint a másikban.

Az alábbi táblázat a Kaplan-Meier-megközelítést használja ugyanazon adatok bemutatására, amelyeket fentebb az élettábla-megközelítéssel mutattunk be. Megjegyezzük, hogy a táblázatot Idő=0 és Túlélési valószínűség = 1 értékkel kezdjük. A Time=0 (kiindulási időpont, vagy a vizsgálat kezdete) időpontjában minden résztvevő veszélyeztetett, és a túlélési valószínűség 1 (vagy 100%). A Kaplan-Meier megközelítéssel a túlélési valószínűség kiszámítása az St+1 = St*((Nt+1-Dt+1)/Nt+1) segítségével történik. Megjegyzendő, hogy a Kaplan-Meier-módszerrel végzett számítások hasonlóak az aktuáriusi élettábla-módszerrel végzett számításokhoz. A fő különbség az időintervallumokban van, azaz a biztosításmatematikai élettábla-megközelítésnél egyenletes időközöket veszünk figyelembe, míg a Kaplan-Meier-megközelítésnél megfigyelt eseményidőpontokat és cenzoridőpontokat használunk. A túlélési valószínűségek számításait a táblázat első néhány sora részletezi.

Élettartam-táblázat Kaplan-Meier megközelítéssel

Idő, Years	Number at Risk Nt	Number of Deaths Dt	Cenzúrázott szám Ct	Túlélési valószínűség St+1 = St*((Nt+1-Dt+1)/Nt+1)
0	20				1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3		3	0.507

Nagy adathalmazok esetén ezek a számítások fárasztóak. Ezek az elemzések azonban olyan statisztikai számítóprogramokkal, mint a SAS, előállíthatók. Az Excel is használható a túlélési valószínűségek kiszámítására, miután az adatokat időpontok szerint rendeztük, és összegeztük az események és a cenzúrázott időpontok számát.

Az élettáblából előállíthatunk egy Kaplan-Meier túlélési görbét.

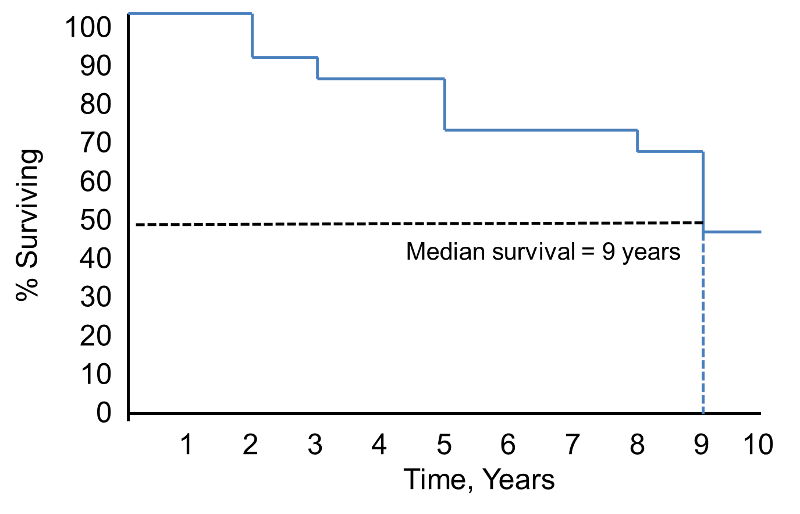
Kaplan-Meier túlélési görbe a fenti adatokhoz

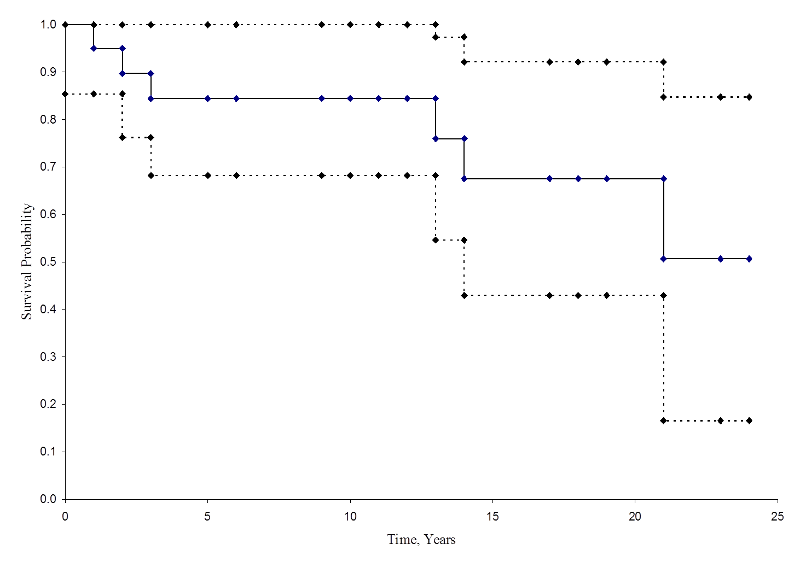
A fenti túlélési görbén a szimbólumok az egyes eseményidőket jelölik, vagy a halálozást, vagy a cenzúrázott időt. A túlélési görbéből megbecsülhetjük annak valószínűségét is, hogy egy résztvevő 10 évnél tovább él, ha a 10 évet az X tengelyen keressük, és az Y tengelyen felfelé és átolvassuk. A 10 évet túlélő résztvevők aránya 84%, a 20 évet túlélő résztvevők aránya pedig 68%. A túlélés mediánját úgy becsüljük meg, hogy az Y tengelyen a 0,5 értéket helyezzük el, és az X tengelyen felfelé és lefelé olvassuk le. A medián túlélés megközelítőleg 23 év.

A túlélési valószínűségek standard hibái és konfidencia-intervallum becslései

A meghatározott időpontokra vonatkozó túlélési valószínűségek és a medián túlélési idő becslései pontbecslések, és ekként kell értelmezni őket. A túlélési valószínűségek standard hibáinak és konfidenciaintervallum becsléseinek előállítására léteznek képletek, amelyek számos statisztikai számítási csomaggal előállíthatók. A túlélési becslések standard hibájának becslésére szolgáló népszerű képlet a Greenwoods5 képlet, amely a következő:

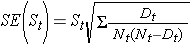
A 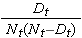mennyiséget összeadjuk a veszélyeztetett számok (Nt) és a halálozások (Dt) számára, amelyek a vizsgált időpontig történtek (azaz kumulatívan, a vizsgált időpontot megelőző összes időpontra, lásd a példát az alábbi táblázatban). A túlélési becslések standard hibáit az alábbi táblázatban szereplő adatokra vonatkozóan számították ki. Vegyük észre, hogy az utolsó oszlopban az 1,96*SE(St) mennyiség szerepel, amely a hibahatár, és amelyet a 95%-os konfidenciaintervallum becslések kiszámításához használnak (azaz St ± 1,96 x SE(St)).

Túlélési becslések standard hibái

Idő, Years	Number at Risk Nt	Number of Deaths Dt	Survival	Survival Valószínűség St				1.96*SE (St)
0	20		1
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0,000	0,118	0,174	0,341

Az alábbi ábrán a becsléseket és a konfidenciaintervallumokat foglalja össze. A Kaplan-Meier túlélési görbe egybefüggő vonalként, a 95%-os konfidenciahatárok pedig szaggatott vonalként vannak feltüntetve.

Kaplan-Meier túlélési görbe konfidenciaintervallumokkal

Kumulatív előfordulási görbék

Néhány vizsgáló a túlélési görbékkel szemben, amelyek a vizsgált esemény bekövetkezésének kumulatív valószínűségét mutatják, inkább kumulatív előfordulási görbéket készít. A kumulatív incidencia vagy kumulatív meghibásodási valószínűség 1-St értékkel számítható, és könnyen kiszámítható az élettáblából a Kaplan-Meier megközelítéssel. A fenti példa kumulatív meghibásodási valószínűségeit az alábbi táblázat mutatja.

Élettartam-táblázat a kumulatív meghibásodási valószínűségekkel

Idő, Years	Number at Risk Nt	Number of Deaths Dt	Number of Deaths Dt	Number of Cenzúrázott Ct	Túlélési valószínűség St	Kudarc valószínűsége 1-St
0	20				1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0,493

Az alábbi ábra a halálozás kumulatív előfordulását mutatja a fent leírt vizsgálatba bevont résztvevők esetében.

Kumulatív előfordulási görbe

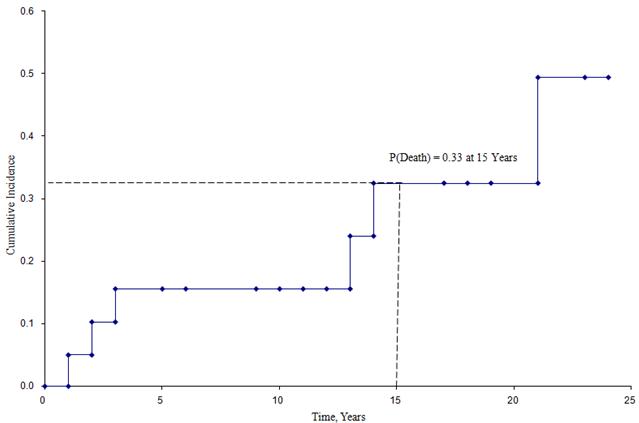
Ez az ábra alapján megbecsülhetjük annak valószínűségét, hogy egy résztvevő egy bizonyos időpontig meghal. Például a halálozás valószínűsége 15 évesen körülbelül 33% (lásd a szaggatott vonalakat).

vissza az oldal tetejére | előző oldal | következő oldal