Gráfok Pythonban

A gráfelmélet eredete

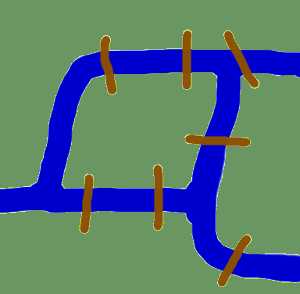Mielőtt a gráfok tényleges implementációival foglalkoznánk Pythonban, és mielőtt a gráfokkal foglalkozó Python modulok bemutatásába kezdenénk, a gráfelmélet eredetének szeretnénk szentelni magunkat.
Az eredet a 18. századi Künigsbergbe vezet vissza minket az időben. Königsberg akkoriban Poroszország egyik városa volt. A Pregel folyó átfolyik a városon, két szigetet hozva létre. A várost és a szigeteket a képen látható hét híd kötötte össze. A város lakóit az a kérdés mozgatta, hogy vajon lehetséges-e úgy végigsétálni a városon, hogy a város minden egyes területét bejárjuk, és minden hídon csak egyszer kelünk át? Minden hídon teljes egészében át kellett menni, azaz nem szabad egy híd felét átsétálni, majd visszafordulni és később a másik felén a másik oldalról átmenni. A sétának nem kell ugyanazon a ponton kezdődnie és végződnie. 1735-ben Leonhard Euler megoldotta a problémát, és bebizonyította, hogy ez nem lehetséges. Rájött, hogy az egyes földterületeken belüli útvonal megválasztása lényegtelen, és csak az számít, hogy milyen sorrendben (vagy sorrendben) megyünk át a hidakon. A probléma absztrakcióját fogalmazta meg, kiküszöbölve a felesleges tényeket, és a szárazföldi területekre és az azokat összekötő hidakra összpontosítva. Ezzel megteremtette a gráfelmélet alapjait. Ha egy “szárazföldi területet” csúcsnak, minden hidat pedig élnek tekintünk, akkor a problémát gráffá “redukáltuk”.

Bevezetés a gráfelméletbe Python használatával

Mielőtt a gráfok lehetséges Python-ábrázolásaival foglalkoznánk, szeretnénk bemutatni a gráfok és összetevőik néhány általános definícióját.
A “gráf “1 a matematikában és az informatikában “csomópontokból”, más néven “csúcsokból” áll.A csomópontok kapcsolódhatnak egymáshoz vagy nem. Ábránkban, – amely egy gráf képi ábrázolása, – az “a” csomópont kapcsolódik a “c” csomóponttal, de “a” nem kapcsolódik a “b”-vel. A két csomópont közötti összekötő vonalat élnek nevezzük. Ha a csomópontok közötti élek nem irányítottak, a gráfot irányítatlan gráfnak nevezzük. Ha egy él az egyik csúcsból (csomópontból) a másikba irányított, a gráfot irányított gráfnak nevezzük. Az irányított éleket ívnek nevezzük.
Bár a gráfok nagyon elméletinek tűnhetnek, sok gyakorlati probléma ábrázolható gráfokkal. Gyakran használják őket problémák vagy helyzetek modellezésére a fizikában, a biológiában, a pszichológiában és mindenekelőtt az informatikában. Az informatikában a gráfokat a kommunikációs hálózatok, az adatszervezés, a számítási eszközök, a számítási folyamat ábrázolására használják,

Ez utóbbi esetben az adatszervezés, például egy operációs rendszer fájlrendszere, vagy a kommunikációs hálózatok ábrázolására. A weboldalak linkstruktúrája is tekinthető gráfnak, azaz irányított gráfnak, hiszen egy link egy irányított él vagy ív.
A Pythonban nincs beépített adattípus vagy osztály a gráfok számára, de Pythonban könnyen megvalósíthatóak. Egy adattípus ideális a gráfok Pythonban való ábrázolására, mégpedig a szótárak. Az ábránkban szereplő gráf a következő módon valósítható meg:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

A fenti szótár kulcsai a gráfunk csomópontjai. A hozzájuk tartozó értékek listák a csomópontokkal, amelyeket egy él köt össze. Ennél egyszerűbb és elegánsabb módja nincs a gráf ábrázolásának.
Egy él tekinthető 2-tuplának, amelynek elemei a csomópontok, azaz (“a”, “b”)
Az összes él listáját generáló függvény:Ez a kód a következő kimenetet generálja, ha a korábban definiált gráfszótárral kombináljuk:

 $ python3 graph_simple.py 

Amint látjuk, nincs olyan él, amely az “f” csomópontot tartalmazza. “f” a gráfunk izolált csomópontja.
A következő Python függvény kiszámítja egy adott gráf izolált csomópontjait:Ha ezt a függvényt a gráfunkkal hívjuk meg, akkor egy “f”-t tartalmazó listát kapunk vissza:

A gráfok, mint Python-osztály

Mielőtt folytatnánk a gráfok függvényeinek megírását, először egy Python gráfosztály implementációját próbáljuk ki. Ha megnézzük az osztályunk alábbi listáját, akkor a __init__-módszerben láthatjuk, hogy egy “self.__graph_dict” szótárat használunk a csúcsok és a hozzájuk tartozó szomszédos csúcsok tárolására.
Ha ezt a modult önállóan indítjuk el, a következő eredményt kapjuk:

Útvonalak a gráfokban

Most meg akarjuk találni a legrövidebb utat egy csomópontból egy másik csomópontba. Mielőtt rátérnénk a feladat Python-kódjára, néhány formális definíciót kell bemutatnunk.
Mellettes csúcsok:
Két csúcs akkor szomszédos, ha mindkettő egy közös élre esik.
Ötvonal egy irányítatlan gráfban:
Egy irányítatlan gráfban az út a csúcsok P = ( v1, v2, …., vn ) ∈ V x V x … x V úgy, hogy vi szomszédos v{i+1}-vel 1 ≤ i < n esetén. Az ilyen P utat a v1-től vn-ig tartó n hosszúságú útnak nevezzük.
Egyszerű út:
Egyszerű útnak nevezzük azt az utat, amelynek nincs ismétlődő csúcsa.
Példa:
(a, c, e) egyszerű út a gráfunkban, csakúgy, mint (a,c,e,b). Az (a,c,e,b,c,d) egy út, de nem egyszerű út, mert a c csomópont kétszer szerepel.
A következő módszer egy kezdőcsúcsból egy végcsúcsba vezető utat talál:Ha a find_path metódust tartalmazó gráf osztályunkat “graphs.py” néven mentjük el, akkor ellenőrizhetjük a find_path függvényünk működésének módját:Az előző program eredménye így néz ki:

A find_all_paths metódus megtalálja az összes utat egy kezdőcsúcs és egy végcsúcs között:Kicsit megváltoztattuk a példagráfunkat úgy, hogy “a”-tól “f”-ig és “f”-től “d”-ig éleket adtunk hozzá, hogy teszteljük a korábban definiált metódust:Az eredmény így néz ki:

fok

A gráfban egy v csúcs fokozata az azt összekötő élek száma, a hurkokat kétszer számolva. Egy v csúcs fokát deg(v)-nek jelöljük. Egy G gráf maximális foka, amelyet Δ(G) jelöl, és minimális foka, amelyet δ(G) jelöl, a gráf csúcsainak maximális és minimális foka.
A jobb oldali gráfban a c csúcsban a maximális fok 5, a minimális fok pedig 0, azaz az f izolált csúcs.
Ha egy gráfban minden fok azonos, akkor a gráf szabályos gráf.
Egy szabályos gráfban minden fok azonos, ezért beszélhetünk a gráf fokáról.
A fokszámösszeg formula (Handshaking lemma):
∑v &in; Vdeg(v) = 2 |E|
Ez azt jelenti, hogy az összes csúcs fokszámának összege egyenlő az élek számának 2-vel való szorzatával.Ebből arra következtethetünk, hogy a páratlan fokszámú csúcsok száma páros kell, hogy legyen. Ezt az állítást kézrázó lemma néven ismerjük. A “kézfogás lemma” elnevezés egy népszerű matematikai problémából származik: Bármely embercsoportban azoknak az embereknek a száma, akik páratlan számú másik emberrel fogtak kezet a csoportból, páros.
A következő módszer kiszámítja egy csúcs fokát:
A következő módszer kiszámítja egy gráf izolált csúcsait tartalmazó listát:A delta és delta módszerekkel kiszámítható egy csúcs minimális, illetve maximális foka:

Fokozatszekvencia

Egy irányítatlan gráf fokozati szekvenciáját úgy definiáljuk, mint a csúcsok fokozati sorrendjét nem növekvő sorrendben.
A következő módszer egy tuple-t ad vissza a példa gráfjának fokozati sorrendjével:
A példánk gráfjának fokszámsorozata a következő egész számok sorozata: (5,2,1,1,1,0).
Az izomorf gráfok fokszámsorozata megegyezik. Két azonos fokszámsorozattal rendelkező gráf azonban nem feltétlenül izomorf.
Felmerül a kérdés, hogy egy adott fokszámsorozat megvalósítható-e egyszerű gráffal. Az Erdös-Gallai-tétel kimondja, hogy egy n számból álló, nem növekvő di (fori = 1, …, n) akkor és csakis akkor egy egyszerű gráf fokszámsorozata, ha a sorozat összege páros, és a következő feltétel teljesül:

Erdös-Gallai tétel megvalósítása

A gráfosztályunk – a teljes felsorolást lásd lejjebb – tartalmaz egy “erdoes_gallai” metódust, amely eldönti, hogy egy sorozat teljesíti-e az Erdös-Gallai-tételt. Először is ellenőrizzük, hogy a sorozat elemeinek összege páratlan-e. Ha igen, akkor a függvény False-t ad vissza, mert az Erdös-Gallai-tétel már nem teljesülhet. Ezután az is_degree_sequence statikus metódussal ellenőrizzük, hogy a bemeneti sorozat fokszámsorozat-e, azaz, hogy a sorozat elemei nem növekvőek. Ez egyfajta felesleges, hiszen a bemenetnek fokszámsorozatnak kell lennie, így ezt az ellenőrzést a hatékonyság kedvéért elhagyhatjuk. Most a második if utasítás testében ellenőrizzük, hogy teljesül-e a tétel egyenlőtlensége:

Változat a felesleges fokszámsorozat vizsgálata nélkül:

Gráf sűrűsége

A gráf sűrűségét egy adott gráf éleinek számának és az összes élek számának arányaként határozzuk meg, amelyekkel a gráf rendelkezhetne. Más szavakkal: Azt méri, hogy egy adott gráf mennyire áll közel a teljes gráfhoz.
A maximális sűrűség 1, ha egy gráf teljes. Ez egyértelmű, mert a gráf éleinek maximális száma a csúcsoktól függ, és a következőképpen számítható ki:
max. élek száma = ½ * |V| * ( |V| – 1 ).
A másik oldalon a minimális sűrűség 0, ha a gráfnak nincsenek élei, azaz izolált gráfról van szó.
Az irányítatlan egyszerű gráfok esetében a gráf sűrűsége a következőképpen definiálható: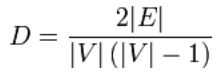

A sűrű gráf olyan gráf, amelyben az élek száma közel van a maximális élek számához. Azt a gráfot, amelynek csak néhány éle van, ritka gráfnak nevezzük. E két fogalom definíciója nem túl éles, azaz nincs legkisebb felső korlát (szupremum) a ritkás sűrűség és nincs legnagyobb alsó korlát (infimum) a sűrű gráf meghatározására.
A legpontosabb matematikai jelölés a nagy O jelölést használja:
Ritkás gráf:
Sűrű gráf:
A sűrű gráf egy olyan G = (V, E) gráf, amelyben |E| = Θ(|V|2).
A “density” az osztályunk egyik metódusa a gráf sűrűségének kiszámítására:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

A módszert a következő szkript segítségével tesztelhetjük. A teljes gráf sűrűsége 1, az izolált gráfé pedig 0, amint azt az előző tesztszkript eredményéből láthatjuk:

$ python test_density.py 0.4666666666671.00.0

Kötött gráfok

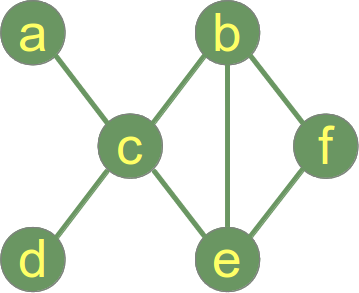Egy gráfot akkor mondjuk összefüggőnek, ha a gráf minden csúcspárja összefüggő. A jobb oldali példagráf egy összefüggő gráf.
Egy egyszerű algoritmussal meghatározható, hogy egy gráf összefüggő-e:

1. Válasszuk ki a G gráf egy tetszőleges x csomópontját kiindulópontnak
2. Meghatározzuk az x-ből elérhető összes csomópont A halmazát.
3. Ha A egyenlő G csomópontjainak halmazával, akkor a gráf összefüggő, ellenkező esetben összefüggéstelen.

Egy is_connected metódust implementálunk annak ellenőrzésére, hogy egy gráf összefüggő gráfnak tekinthető-e. Nem a hatékonyságra, hanem az olvashatóságra helyezzük a hangsúlyt.
Ha ezt a metódust hozzáadjuk a gráf osztályunkhoz, akkor a következő szkript segítségével tesztelhetjük. Feltételezve, hogy a graph osztályt graph2.py néven mentettük el:
Egy összefüggő komponens G egy maximálisan összefüggő részgráfja. Minden csúcs pontosan egy összefüggő komponenshez tartozik, ahogy minden él is.

Distance and Diameter of a Graph

A gráf két csúcsa közötti “dist” távolság az e csúcsok közötti legrövidebb út hossza. A távolság kiszámításánál nem engedélyezettek a visszautak, kerülőutak vagy hurkok.
Jobb oldali példagráfunkban az a és az f csúcs közötti távolság 3, azaz dist(a,f) = 3, mert a legrövidebb út a c és e (vagy c és b felváltva) csúcsokon keresztül vezet.
A g gráf egy s csúcsának excentricitása a gráf minden más csúcsától mért maximális távolság:
e(s) = max( { dist(s,v) | v ∈ V })
(V a g összes csúcsának halmaza)
A gráf d átmérőjét a gráf bármelyik csúcsának maximális excentricitásaként határozzuk meg. Ez azt jelenti, hogy az átmérő a legtávolabbi csomópontok közötti legrövidebb út hossza. Egy gráf átmérőjének meghatározásához először keressük meg az egyes csúcspárok közötti legrövidebb utat. Ezen utak bármelyikének legnagyobb hossza a gráf átmérője.
Példagráfunkban közvetlenül láthatjuk, hogy az átmérő 3, mert az a és f közötti legkisebb hossz 3, és nincs más olyan csúcspár, amelynek útja ennél hosszabb lenne.
A következő módszer egy algoritmust valósít meg az átmérő kiszámítására. A példagráfunk átmérőjét a következő szkripttel tudjuk kiszámítani, ismét feltételezve, hogy a teljes gráfosztályunkat graph2.py néven mentettük:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Ez kiírja a 3 értéket.

A teljes Python gráfosztály

A következő Python kódban a teljes Python osztálymodul található az összes tárgyalt metódussal:graph2.py

Fa / Erdő

A fa egy irányítatlan gráf, amely nem tartalmaz ciklusokat. Ez azt jelenti, hogy a gráf bármely két csúcsát pontosan egy egyszerű út köti össze.
Az erdő fák diszjunkt uniója. A természetben előforduló erdőkkel ellentétben a gráfelméletben egy erdő egyetlen fából is állhat!
Az egy csúcsot tartalmazó, él nélküli gráf egy fa (és egy erdő).
Egy példa a fára: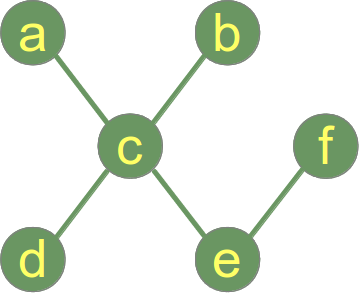

Míg az előző példa egy olyan gráfot ábrázol, amely egy fa és egy erdő, addig a következő kép egy olyan gráfot mutat, amely két fából áll, azaz i.azaz a gráf egy erdő, de nem fa:

Az erdők áttekintése:

Egy csúccsal:

Erdős gráfok két csúccsal:

Három csúccsal rendelkező erdei gráfok:

Terjedési fa

Egy összefüggő, irányítatlan G gráf T terjedési fája G egy olyan részgráfja, G’, amely egy fa,és G’ tartalmazza G összes csúcsát és éleinek egy részhalmazát. G’ tartalmazza G összes élét, ha G egy fa gráf. Informálisan G áthidaló fája G éleinek olyan kiválasztása, amely minden csúcson áthidaló fát alkot. Vagyis minden csúcs a fában fekszik, de nem tartalmaz ciklust (vagy hurkot).
Példa:
Egy teljesen összefüggő gráf: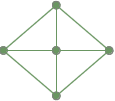

Két átfutófa az előző teljesen összefüggő gráfból: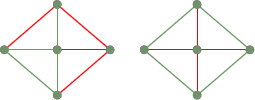

Hamilton-játék

A Hamilton-út olyan út egy irányítatlan vagy irányított gráfban, amely minden csúcsot pontosan egyszer látogat meg. A Hamiltoni ciklus (vagy kör) egy olyan Hamiltoni út, amely egy ciklus.
Jegyzet informatikusok számára: Általában nem lehet megállapítani, hogy léteznek-e ilyen utak vagy ciklusok tetszőleges gráfokban, mert a Hamilton-út probléma bizonyítottan NP-teljesnek bizonyult.
Nevét William Rowan Hamiltonról kapta, aki feltalálta az úgynevezett “ikszoszi játékot”, vagy Hamilton rejtvényét, amely a dodekaéder élgráfjában egy Hamiltoni ciklus megtalálását jelenti. Hamilton ezt a feladatot az ikóziánus számítással oldotta meg, amely egy olyan algebrai struktúra, amely az egységgyökökön alapul, és sok hasonlóságot mutat a kvaternionokkal, amelyeket szintén ő talált fel.

A Graph osztály teljes listázása

A Graph osztályt a következő programmal tesztelhetjük:Ha ezt a programot elindítjuk, a következő kimenetet kapjuk:
Lábjegyzetek:
1 A gráfelméletben (és Python oktatókönyvünk ezen fejezetében) vizsgált gráfok nem tévesztendők össze a függvények gráfjaival
2 A singleton olyan halmaz, amely pontosan egy elemet tartalmaz.
Hiteltérítés:
Narayana Chikkam, nchikkam(at)gmail(dot)com, rámutatott egy indexhibára az “erdoes_gallai” módszerben. Köszönjük szépen, Narayana!