Aristotelész (Ἀριστοτέλης) Kr. e. 384-322 között született görög filozófus és tudós a klasszikus görögországi Sztagira városában.

Tizenhét évesen belépett Platón athéni akadémiájába, és harminchét éves koráig (i. e. 347 körül)

Az írásai számos témakört – többek között fizika, biológia, zoológia, logika, etika, költészet, színház, zene, nyelvészet és politika – érintenek. Ezek alkotják a nyugati filozófia első átfogó rendszerét.

• Az Arisztotelésztől átvett és átvett szövegek. (2016. október 20.). Wikipedia, The Free Encyclopedia.

Arisztotelész 3 mozgástörvényt fogalmazott meg, amelyek megfigyeléseken alapulnak (de nem kísérleteken)

* Az égitestek (az éggömb) körkörös mozgást végeznek,anélkül, hogy bármilyen külső erő erre kényszerítené őket.a földi tárgyak (a földi szféra) egyenes vonalban mozognak,hacsak nem kényszerítik őket körkörös mozgásra.

Mi a helyzet a tolással és a húzással?

természetes vs. természetellenes mozgás

Mi történne tehát, ha egy ágyú kilőne egy ágyúgolyót? Arisztotelész feltételezte, hogy egyenes vonalban mozogna (a természetellenes erő miatt), majd egyenesen lefelé esne (egy másik, természetes erő miatt.)

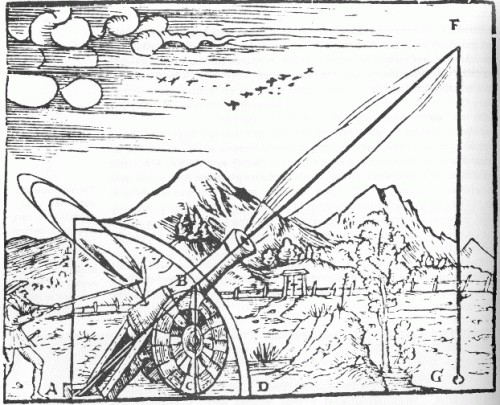
Arisztotelész számára, miután az “erőszakos mozgás” (az emberektől) kioltotta magát, a természetes mozgás veszi át a hatalmat, és akkor az ágyúgolyó a természetes helyére, a földre esik.

Amint azonban Galielo az 1500-as években megmutatta, Arisztotelész nézete egyáltalán nem helyes. Bárki, aki figyeli, ahogy egy íjász kilő egy nyilat a levegőbe, és figyelmesen megfigyeli, láthatja, hogy ez nem így történik.

A függőleges mozgás lassan csökken, eléri a nullát (a csúcson), majd az ellenkező (lefelé irányuló) irányban növekszik.

A mennyei erők vs. földi erők

A földi (földi) tárgyakról azt hitték, hogy külön mozgástörvényekkel rendelkeznek. A földi tárgyak állítólag mindig megállnak a mozgásban, maguktól, maguktól.

* a tárgyak természetesen csak egyenes vonalban mozognak.* a tárgyak körkörös mozgásához valamilyen külső erőre van szükség,ami körkörös pályára húzza őket

Akár Arisztotelész soha nem végzett kísérleteket, így nagyon korlátozott volt abban, hogy mit tudott megfigyelni.A középkorban Galilei (és mások) ellenőrzött kísérleteket végeztek.E kísérletek eredményeit matematikával elemezték.

Galileo az apjától, Vincenzótól

a. Amikor a golyó lefelé gurul, a Föld gravitációjával mozog, és sebessége megnő.

c. Amikor a golyó síkban gurul, nem mozog sem a gravitációval, sem a gravitációval szemben.

b. Ahogy a felfelé irányuló lejtő szöge csökken,a golyó nagyobb távolságot gurul, mielőtt elérné a kezdeti magasságát.

Galileo következtetését egy másik gondolatmenet is alátámasztotta.

Ferde sík – Galilei harca a mennyekért PBS NOVA

Golyók, hengerek és csövek gurítása a ferde síkon: A tehetetlenségi nyomaték

Egy különleges dolog: A brachistochrone – a leggyorsabb süllyedés görbéje. És a tautokrón – az a görbe, amelynél az egyenletes gravitációban súrlódás nélkül csúszó tárgynak a legalacsonyabb pontjáig eltelt idő független a kiindulási ponttól.

Aristotelész mozgástörvényei.

Kivonat Michael Fowler professzor előadásából, U. Va. Physics, 9/3/2008

http://galileoandeinstein.physics.virginia.edu/lectures/aristot2.html

Az, amit Arisztotelész azokban az athéni években elért, az az volt, hogy a szervezett tudományos kutatás olyan méretű iskoláját indította el, amely messze felülmúlta mindazt, ami előtte volt. Először is világosan meghatározta, mi a tudományos ismeret, és miért kell azt keresni. Más szóval, egyedül ő találta fel a tudományt, mint a mai kollektív, szervezett vállalkozást. Platón Akadémiájának volt egy egyetemi matematika tanszéknek megfelelője, Arisztotelésznek volt az első természettudományi tanszéke, amely valóban kiváló volt a biológiában, de, mint látni fogjuk, kissé gyenge a fizikában.

Arisztotelész után több mint 2000 évig nem volt hasonló professzionális tudományos vállalkozás, és az ő munkája olyan színvonalú volt, hogy mindenki elfogadta, és 2000 évvel később már régóta része volt a keresztény egyház hivatalos ortodoxiájának. Ez nem volt szerencsés, mert amikor Galilei megkérdőjelezte az egyszerű fizikára vonatkozó egyes állításokat, hamarosan komoly bajba került az egyházzal.
Aristotelész vizsgálati módszere:

meghatározza a témát

felméri a felmerülő nehézségeket, áttekintve a témával kapcsolatos általánosan elfogadott nézeteket és a korábbi szerzők javaslatait

előadja saját érveit és megoldásait

Ez a modern kutatási dolgozatok mintája, Arisztotelész lefektette a tudományos kutatás szokásos szakmai megközelítését.

Aristotelész gyakran úgy cáfolt meg egy ellenérvet, hogy kimutatta, hogy az abszurd következtetéshez vezet, ezt nevezik reductio ad absurdumnak (valamit abszurdumra redukál). Mint később látni fogjuk, Galilei pontosan ilyen érvelést használt maga Arisztotelész ellen, az arisztotelészek nagy bosszúságára 2000 évvel Arisztotelész után.

Platónnal ellentétben, aki úgy vélte, hogy az egyetlen érdemleges tudomány az elvont formák szemlélése, Arisztotelész a növények és állatok részletes megfigyelését és boncolását gyakorolta, hogy megpróbálja megérteni, hogyan illeszkedik mindegyik a természet nagy rendszerébe, és milyen fontosak az állatok különböző szervei.

El kell ismernünk, hogy a világ, amelyet Arisztotelész a mindennapi életben maga körül látott, valóban nagyon különbözött attól, amit ma látunk. Minden modern gyermek születése óta látja a körülötte mozgó autókat és repülőgépeket, és hamar rájön, hogy ezek a dolgok nem élnek, mint az emberek és az állatok. Ezzel szemben a negyedik századi Görögországban a legtöbb mozgást emberek, állatok és madarak látták, amelyek mind nagyon is élők voltak. Ezeknek a mozgásoknak mind céljuk volt, az állat valamilyen oknál fogva egy olyan helyre ment, ahol szívesebben lenne, tehát a mozgást az állat akarata irányította.

Arisztotelész számára ez a mozgás tehát az állat “természetét” teljesítette, ahogyan a természetes növekedése is az állat természetét teljesítette.

A nyilvánvalóan nem élő dolgok, például egy kézből elejtett kő mozgásának magyarázatára Arisztotelész kiterjesztette a valami “természetének” fogalmát az élettelen anyagra. Azt javasolta, hogy az ilyen élettelen tárgyak mozgását úgy lehet megérteni, ha azt tételezzük fel, hogy az elemek hajlamosak a dolgok rendjében a természetes helyüket keresni:

A föld tehát lefelé mozog a legerősebben,
a víz is lefelé áramlik, de nem olyan erősen, mivel a kő a vízen keresztül esik.
A levegő ezzel szemben felfelé mozog (buborékok a vízben),
és a tűz halad felfelé a legerősebben, mivel a levegőn keresztül felfelé lövell.

Az elemek mozgásának ezt az általános elméletét természetesen ki kell dolgozni, amikor valós anyagokra alkalmazzuk, amelyek elemek keverékei. Arra a következtetésre jutna, hogy a fában föld és levegő is van, mivel nem süllyed el a vízben.

Természetes mozgás és erőszakos mozgás

A dolgok azért is mozognak, mert lökik őket. Egy kő természetes hajlama, ha magára hagyjuk és nem támasztjuk, az, hogy leesik, de mi felemelhetjük, vagy akár a levegőbe is dobhatjuk.

Aristotelész az ilyen kényszerített mozgást “erőszakos” mozgásnak nevezte, szemben a természetes mozgással.

Az “erőszakos” kifejezés csak azt jelenti, hogy valamilyen külső erő hat rá.

Aristotelész volt az első, aki kvantitatív módon gondolkodott az ilyen mozgások sebességéről. Két kvantitatív állítást tett arról, hogyan esnek a dolgok (természetes mozgás):

A nehezebb dolgok gyorsabban esnek, a sebesség arányos a súlyukkal.

Egy adott tárgy esési sebessége fordítottan függ a közeg sűrűségétől, amelyen keresztül esik.

Így például ugyanaz a test kétszer olyan gyorsan esik egy feleakkora sűrűségű közegen keresztül.

Megjegyezzük, hogy ezeknek a szabályoknak van egyfajta eleganciájuk, egy vonzó mennyiségi egyszerűségük. És ha leejtünk egy követ és egy papírdarabot, egyértelmű, hogy a nehezebb dolog valóban gyorsabban esik, és a vízen keresztül zuhanó követ a víz határozottan lelassítja, így a szabályok elsőre hihetőnek tűnnek.

A meglepő az, hogy Arisztotelész annyi mindenre vonatkozó aprólékos megfigyelései mellett nem ellenőrizte komolyan ezeket a szabályokat.

Nem tartott volna sokáig kideríteni, hogy például egy fél tégla fele akkora sebességgel esik le, mint egy egész tégla. Nyilvánvalóan ezt nem tartotta fontosnak.

A fenti második állításból arra következtetett, hogy vákuum nem létezhet, mert ha létezne, mivel sűrűsége nulla, akkor minden test végtelen sebességgel esne át rajta, ami nyilvánvalóan képtelenség.

A heves mozgásra vonatkozóan Arisztotelész azt állította, hogy a mozgó tárgy sebessége egyenes arányban áll az alkalmazott erővel.

Ez először is azt jelenti, hogy ha abbahagyjuk a nyomást, a tárgy nem mozog tovább.

Ez bizonyára ésszerű szabálynak hangzik, mondjuk,
ha egy könyvekkel teli dobozt tolunk át egy szőnyegen, vagy ha egy ökör húzza az ekét a mezőn.

(Ez az intuitívan tetszetős kép azonban nem veszi figyelembe
a doboz és a szőnyeg közötti nagy súrlódási erőt.
Ha a dobozt szánkóra tennénk, és a jégen keresztül tolnánk,
nem állna meg, amikor abbahagyjuk a tolást.
Századokkal később Galilei felismerte a súrlódás fontosságát ezekben a helyzetekben.)

Tanulási követelmények

2016 Massachusetts Science and Technology/Engineering Curriculum Framework
HS-PS2-1. Elemezzen adatokat annak az állításnak az alátámasztására, hogy Newton második mozgástörvénye egy
matematikai modell, amely leírja a tárgyak mozgásának változását (a gyorsulást), amikor
egy nettó erő hat rájuk.

HS-PS2-10(MA). Használja a szabadtest-erő diagramokat, algebrai kifejezéseket és Newton mozgástörvényeit, hogy megjósolja a sebesség és a gyorsulás változását egy egy dimenzióban mozgó tárgy esetében különböző helyzetekben

Massachusetts történelem és társadalomtudományok tantervi kerete

A nyugati civilizáció gyökerei: Az ókori Görögország, Kr. e. 800-300.
7.34 Ismertesse a görög intézmények, például a líceum, a gimnázium és az alexandriai könyvtár céljait és fejlődésének funkcióit, és határozza meg az ókori görögök főbb vívmányait.

WHI.33 Foglalja össze, hogyan vezetett a tudományos forradalom és a tudományos módszer a világegyetem új elméleteihez, és ismertesse a tudományos forradalom vezető alakjainak, köztük Bacon, Kopernikusz, Descartes, Galilei, Kepler és
Newton teljesítményeit.

Keretrendszer a K-12-es természettudományos oktatáshoz: gyakorlatok, átfogó fogalmak és alapgondolatok
PS2.A: ERŐK ÉS MOZGÁS
Hogyan lehet megjósolni egy tárgy folyamatos mozgását, mozgásváltozását vagy stabilitását?

Egy tárgy és egy másik tárgy kölcsönhatása magyarázható és megjósolható az erők fogalmával, amelyek az egyik vagy mindkét kölcsönható tárgy mozgásában változást okozhatnak… Makroszinten az erőknek kitett tárgyak mozgását Newton második mozgástörvénye szabályozza… A tárgyak közötti erők megértése fontos annak leírásához, hogyan változik a mozgásuk, valamint a rendszerek stabilitásának vagy instabilitásának megjóslásához bármilyen léptékben.