Míg számos légköri paraméter befolyásolja a külső szigetelés dielektromos szilárdságát, a relatív légsűrűség (δ) és az abszolút páratartalom tekinthető a legjelentősebbnek. Itt az előbbi áll a középpontban, amely kulcsszerepet játszik a nagy magasságban lévő átviteli rendszerek fejlesztésében, mint például Kínában 5000 m-ig. A légsűrűség szerepének tanulmányozása több mint egy évszázaddal ezelőtt kezdődött, de felgyorsult az EHV fejlődésével és a vezeték- és alállomások tervezésének optimalizálásának szükségességével kapcsolási túlfeszültségek mellett. Nagy magassági vizsgálatokat végeztek nagy távolságokon Oroszországban (1967 Bazeylan & 1968 Volkova és mtsi.: vizsgálatok 3370 m-ig), az USA-ban (1967 Phillips és mtsi.: vizsgálatok 3500 m-ig), Japánban (Harada és mtsi. 1970: vizsgálatok 1850 m-ig), valamint Olaszországban, Dél-Afrikában és Mexikóban (Pigini és mtsi. 1989: összehasonlító vizsgálatok 3000 m-ig). Az újabb kutatások abból az igényből fakadtak, hogy Kínában nagy magasságokban optimalizálni kell az UHV-projektek tervezését, szisztematikus tesztekkel Wuhan (35 m), Peking (50 m), Chengdu (500 m), Yinchuan (1000) m, Lanzhong (1500 m), Kunming (2100 m), Xining (2260) m, Qinghai (3000) m és Tibet (4300 m) területén. Nagyméretű klímakamrákat, mint például a kínai EPRI-nél, építettek 6000 m magasságig terjedő magasságok szimulálására.
A szabványokban különböző megközelítések születtek arra vonatkozóan, hogy miként lehet figyelembe venni a magassággal változó légsűrűséget. Az IEC 60060-1 például, amelyet a laboratóriumi vizsgálatok korrekciójára terveztek, a következőket használja: U=Uo*K, ahol U és Uo a dielektromos szilárdság nagy magasságban, illetve normál légköri körülmények között, és ahol K a K=δm által megadott légsűrűség-korrekciós tényező, ahol δ a relatív légsűrűség a nagy magasságban. Az IEC 60071-2, amelyet a szigetelés koordinálására terveztek, közvetlen hivatkozást tesz a magasságra (H), amely egyszerűsített feltételezések szerint δ a δ=e(H/8150) által a H-hoz viszonyított δ=e(H/8150). A fő probléma az m paraméter meghatározása, amely függ a feszültségterhelés típusától, a szigetelés konfigurációjától, a szigetelő típusától és a környezeti körülményektől (pl. száraz, nedves, szennyezett). Az 1. ábra példát mutat a különböző kutatók által a pozitív kapcsolási impulzusra talált “m” értékek tartományára különböző szigetelőkkel és szigetelők nélküli konfigurációk esetében. Az eredmények a hézagköz függvényében vannak ábrázolva. Ugyanezen az ábrán a folytonos görbék a régi IEC 60-ban elfogadott korrekciós megközelítést képviselik, amely az m értéket a hézagközhöz viszonyítja. Az IEC 60060 és 60071 szabványok szerinti újabb megközelítés a rendelkezésre álló (akkor 3500 m-re korlátozott) információk jobb racionalizálására tett kísérletet, amely az m tényezőt a távolság helyett a feszültségparaméterekhez kapcsolja. A két megközelítés azonban néha ellentmondásos, még akkor is, ha ugyanazokból az alapadatokból indulnak ki, és nehezen is alkalmazhatók. Ráadásul nem veszik figyelembe az 5000 m-ig terjedő vizsgálatokból származó információkat. Ezért szükség volt az ilyen korrekciós megközelítések frissítésére és harmonizálására a legújabb eredmények figyelembevétele mellett, ahogyan azt az IEC ajánlotta és a CIGRE támogatta, ahol munkacsoportok vizsgálták a magasság hatását a tiszta szigetelőkre (WG D1.50) és a szennyezett szigetelőkre (WG D1.44).
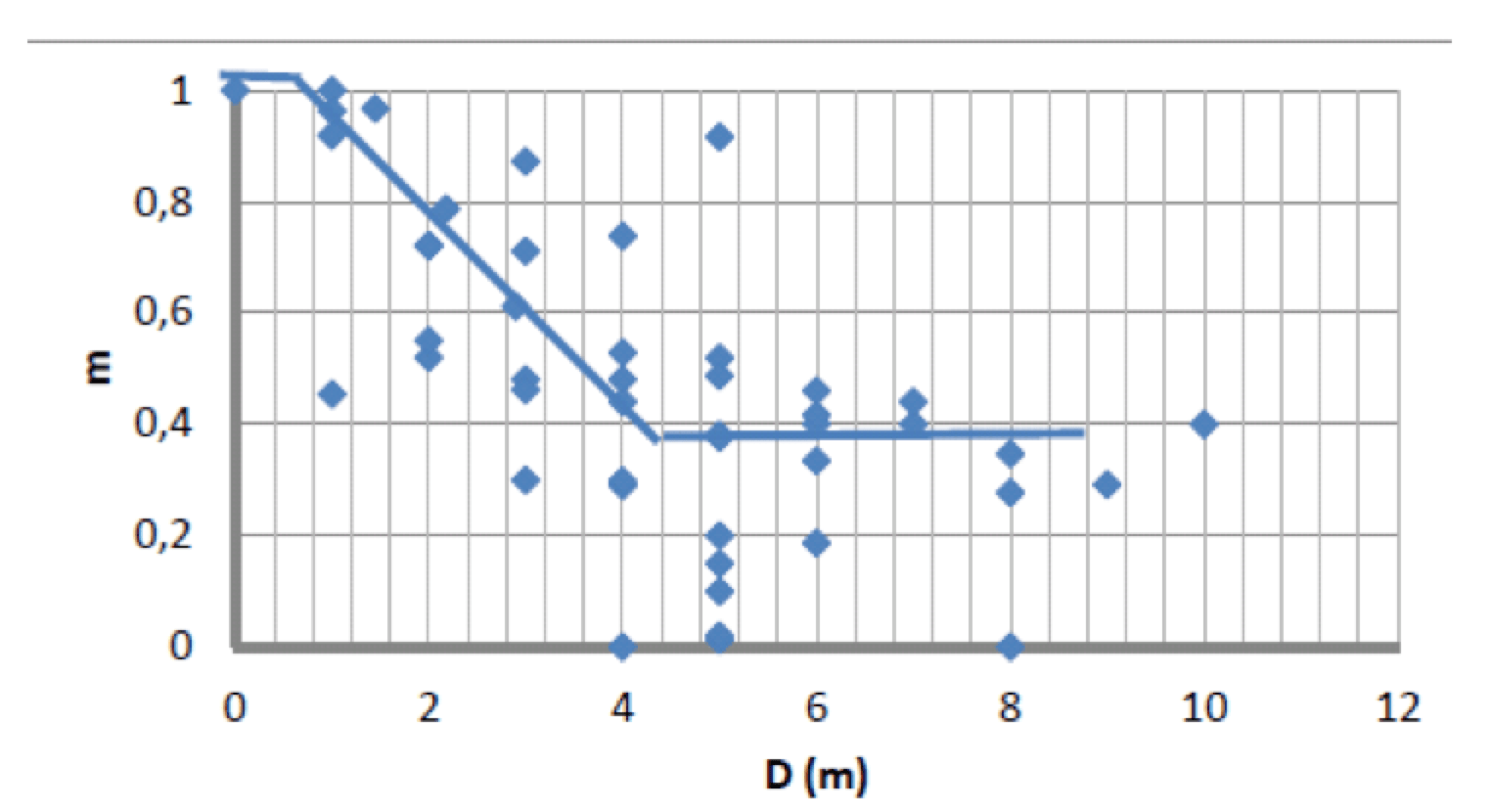
KATTINTSON A NAGYÍTÁSHOZ
Az új megközelítés optimalizálásának több módja van:
1. A légsűrűség hatása általában az átütési/flashover-feszültségnek egy kisebb része: a mérés, a konfigurációs szimuláció vagy a feszültségparaméterek valóban kis pontatlansága jelentős pontatlanságot eredményezhet az m paraméterben, amikor az eredményeket különböző magasságokban összehasonlítjuk. A különböző magasságokban végzett összehasonlító vizsgálatokat ezért pontosan kell megtervezni és elvégezni.
2. A legjobb, ha nem hagyjuk figyelmen kívül a történelmi kísérleti adatok meglévő körét, és az újonnan generált adatokat felhasználjuk azok jobb integrálására és végrehajtására.
3. Számos vizsgálatot végeztek olyan alapkonfigurációkon, mint a rúdsík, száraz körülmények között, ahol a levegő sűrűségének hatása jelentősen eltérhet a tényleges szigetelőkonfigurációkétól. A tényleges konfigurációkra vonatkozóan a lehető legtöbb új adatot kell szolgáltatni.
4. A tervezés során figyelembe veendő egyik legfontosabb környezeti feltétel az eső alatti teljesítmény, amely a feszültségtől, a konfigurációtól és a szigetelő típusától függően drámaian csökkentheti a szigetelő szilárdságát. Mivel a levegő sűrűségének a szigetelő szilárdságára gyakorolt relatív hatása változhat eső alatt, ennek jobb megértéséhez több adatra lehet szükség (pl. a szigetelők egyenfeszültség és eső alatti teljesítményének kutatásával).
5. Mivel az egyenáramú rendszereknél a szennyezés az irányadó tervezési feszültség, további adatokra van szükség a légsűrűségnek a hidrofil, valamint a hidrofób szigetelők szennyezés általi átcsapódására gyakorolt hatásáról a geometria függvényében.
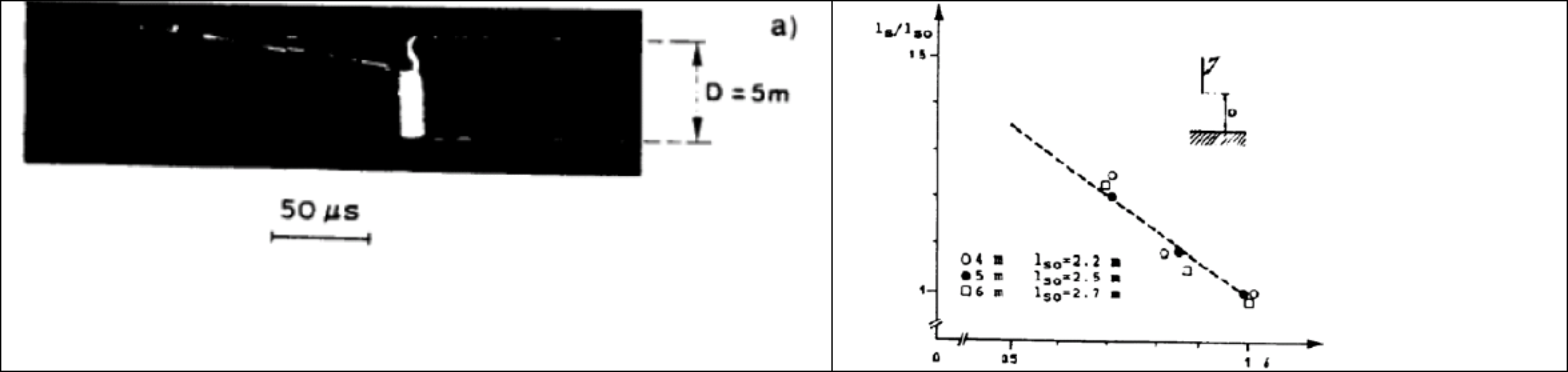
6. A jelenség összetettsége és a sok érintett paraméter miatt a légsűrűség hatásának megértését megkönnyítheti, ha a légsűrűségnek a flashoverhez vezető fizikai folyamatokra gyakorolt hatásának elemzésével párosul, beleértve a streamer- és a vezérfázisra gyakorolt hatását is.
7. E bonyolultság miatt nem tűnik lehetségesnek egyetlen olyan megközelítéshez jutni, amely egyszerre pontos és viszonylag egyszerű. Végső soron az egyszerűségnek kell a mérnöki alkalmazásoknál a célnak lennie, és a szükséges pontosságot a kísérleti eredmények tipikus szórásának vizsgálatával lehetne értékelni.
8. Amennyire lehetséges, a “formális” megközelítésnek azonosnak kell lennie minden különböző szabványban, hogy elkerülhető legyen a jelenlegi szabványok zavara, amelyek gyakran ugyanazt a fogalmat fejezik ki és hasonló jelzéseket adnak, de különböző nyelvezetet használnak.
KATTINTSON A NAGYÍTÁSHOZ