Az elején általában a ciklus pV-diagramjáról kell képet alkotni. Ehhez az izokorikus és az adiabatikus folyamatok görbéit követjük nyomon. Az Otto-ciklus közelítő grafikonját az alábbi ábra mutatja.

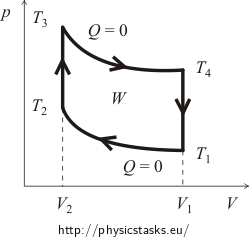
A ciklus η hatásfokát a következőképpen határozzuk meg:

\

ahol W a gáz által egy ciklus alatt végzett munka mínusz a külső erők által végzett munka (az ábrán a ciklus vonalai által meghatározott terület felülete ábrázolja!) és Qsup a rendszerbe a ciklus alatt bevitt hő.

A W munka kiszámítható az adiabatikus tágulás és sűrítés során a nyomás és a térfogat közötti összefüggés segítségével (az izokorikus folyamat során végzett munka természetesen nulla). Ebben a feladatban azonban célszerűbb lesz azt a tényt használni, hogy a belső energia ciklusonkénti teljes változásának egyenlőnek kell lennie nullával (ugyanabba az állapotba jutunk vissza, mint az elején, tehát a hőmérséklet és így a belső energia is ugyanaz marad!). Az első termodinamikai törvény szerint a gáz által végzett munka a Qsup leadott és a Qrel leadott hő különbségeként fejezhető ki. A ciklus hatásfokára vonatkozó képlet tehát a

\

formulát \

\

Először is számítsuk ki a Qsup leadott hőt. Világos, hogy az adiabatikus folyamat során nincs hőcsere, az izokorikus hűtés során pedig a hő felszabadul. Ez azt jelenti, hogy a hő csak az izochorikus fűtés során a T2 hőmérséklettől a T3 hőmérsékletig szállítja a hőt. Ennek a hőnek a mennyisége a gáz n anyagmennyiségének és CV moláris hőkapacitásának változóival a következőképpen fejezhető ki:

\

A felszabaduló hő mennyiségét Qrel hasonló módon fogjuk kifejezni. Azt már tudjuk, hogy a hő csak a T4 hőmérsékletről a T1 kiindulási hőmérsékletre való izochorikus visszahűlés során szabadul fel. Igaz, hogy:

\

Most ezeket a képleteket behelyettesítjük a ciklus hatásfokának képletébe, és azonnal megkapjuk:

\ \ \

Most a hőmérsékletkülönbségeket kell kifejeznünk a megadott sűrítési arány

\

és a κ Poisson-szám segítségével.

Ezért az adiabatikus folyamaton átmenő ideális gázra vonatkozó egyenletet (a Poisson-törvényt) pVκ = C = konst.., ahol C egy konstans. Most egy ideális gáz állapotegyenletéből

\

kiértékeljük a nyomást, amit behelyettesítünk a Poisson-törvénybe. Most a konstansokat (C és K) áthelyezzük az egyik oldalra

\

Most ezt a Poisson-törvényt alkalmazzuk mindkét adiabatikus folyamatra. Az adiabatikus tágulásra megkapjuk az összefüggést

\

Az adiabatikus tömörülésre pedig megkapjuk

\

Most kivonjuk a második egyenletet az elsőből, és az egyik oldalon V1κ – 1, a másikon V2κ – 1 faktoráljuk. Megkapjuk:

\ \ \

Láthatjuk, hogy a megadott értékek segítségével valóban sikerült kifejeznünk a hőmérsékletkülönbségeket. Most ezt az összefüggést behelyettesítjük a hatásfok képletébe, és megkapjuk a végső egyenletet:

\ \ \