Kolmogorov-Smirnov teszt
A K-S teszt egy olyan illeszkedésjósági teszt, amelyet egy adateloszláshalmaz egyenletességének értékelésére használnak. A chi-négyzet-teszt hiányosságaira válaszul fejlesztették ki, amely csak diszkrét, bontott eloszlások esetén ad pontos eredményeket. A K-S teszt előnye, hogy nem tesz feltevést az összehasonlítandó adathalmazok binneléséről, így kiküszöböli a bináris kiválasztás folyamatával járó önkényes jelleget és információvesztést.
A statisztikában a K-S-próba az egyetlen változó függvényében függő folytonos adathalmazok (nem binnelt adateloszlások) közötti különbségek mérésére elfogadott teszt. Ezt a különbségmérőt, a K-S \(D\) statisztikát két kumulatív eloszlásfüggvény közötti abszolút különbség maximális értékeként határozzák meg. Az egyoldalú K-S tesztet egy adatsor és egy ismert kumulatív eloszlásfüggvény összehasonlítására használják, míg a kétoldalú K-S teszt két különböző adatsort hasonlít össze. Minden adathalmaz különböző kumulatív eloszlásfüggvényt ad, és ennek jelentősége a valószínűségi eloszláshoz való viszonyában rejlik, amelyből az adathalmaz származik: az egyetlen független változó \(x\) valószínűségi eloszlásfüggvénye egy olyan függvény, amely valószínűséget rendel \(x\) minden egyes értékéhez. Az \(x_{i}\) adott értéke által feltételezett valószínűség a valószínűség-eloszlásfüggvény \(x_{i}\) értéke, amelyet \(P(x_{i})\) jelöl.A kumulatív eloszlásfüggvényt úgy definiáljuk, hogy az \(x_{i}\) adott értéktől balra eső adatpontok hányadát adja meg, \(P(x <x_{i})\); azt a valószínűséget mutatja, hogy \(x\) kisebb vagy egyenlő egy adott \(x_{i}\) értéknél.
Így két különböző kumulatív eloszlásfüggvény \(S_{N1}(x)\) és \(S_{N2}(x)\) összehasonlítására a K-S statisztika
D = max|S_N1(x) – S_N2(x)|
ahol \(S_{N}(x)\) annak a valószínűségi eloszlásnak a kumulatív eloszlásfüggvénye, amelyből egy \(N\) eseményeket tartalmazó adathalmaz húzódik. Ha \(N\) rendezett események \(x_{i}\) adatpontokban találhatók, ahol \(i = 1, \ldots, N\), akkor
S_N(x_i) = (i-N)/N
ahol az \(x\) adatsor növekvő sorrendben van rendezve. Ez egy lépésfüggvény, amely minden egyes rendezett adatpont értékénél \(1/N\) értékkel növekszik.
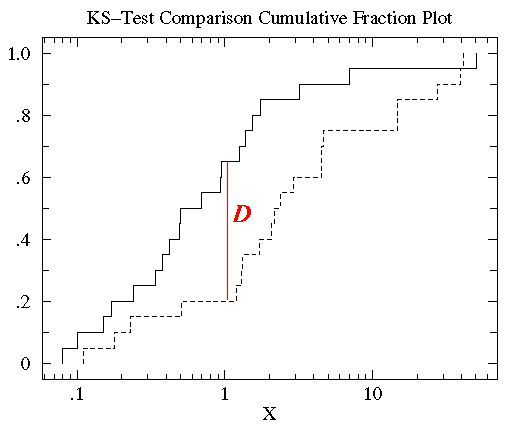
Kirkman, T.W. (1996) Statistists to Use.
http://www.physics.csbsju.edu/stats/
Céljaink szempontjából a két összehasonlított eloszlás az érkezési idők mért eloszlása, illetve az eltelt időintervallumon felhalmozott hányad. Ha a nullhipotézis (nincs változékonyság) érvényes, akkor az eltelt idő 50%-ában kapjuk az eseményeinek 50%-át, és a \(D\) statisztikának az érkezési idők eloszlásának sok realizációja esetén a Kolmogorov-eloszlás szerint kell eloszlania. A teszt által visszaadott valószínűség tehát \(p_{KS} = 1 – \alpha\), ahol \(\alpha\) annak a valószínűsége (a Kolmogorov-eloszlás szerint), hogy az \(D\) értéke nagyobb vagy egyenlő a mért értéknél. Az \(p_{KS}\) kis értéke tehát a nullhipotézisnek való megfelelést jelzi, míg az \(p_{KS}\) nagy értéke azt jelzi, hogy az események közötti intervallum nem állandó, és ezért a változékonyságra lehet következtetni.