6.3 Hiedelemhálózatok
A feltételes függetlenség fogalma számos tartomány tömör reprezentációjára használható. Az elképzelés lényege, hogy adott egy véletlenszerű X változó, létezhet olyan változók kis halmaza, amelyek közvetlenül befolyásolják a változó értékét abban az értelemben, hogy X feltételesen független a többi változótól, ha a közvetlenül befolyásoló változók értékei adottak. A helyileg befolyásoló változók halmazát Markov-takarónak nevezzük. Ezt a lokalitást használják ki a hiedelemhálózatban. A hiedelemhálózat a véletlen változók egy halmaza közötti feltételes függőség irányított modellje. A feltételes függetlenség pontos kijelentése a hiedelemhálózatban figyelembe veszi az irányítottságot.
A hiedelemhálózat meghatározásához kezdjük a modell összes jellemzőjét reprezentáló véletlen változók halmazával. Tegyük fel, hogy ezek a változók {X1,…,Xn}.Ezután válasszuk ki a változók teljes sorrendjét, X1,…,Xn.
A láncszabály (6.3. tétel) megmutatja, hogyan lehet egy konjunkciót feltételes valószínűségekre bontani:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Vagy a véletlen változók és valószínűségi eloszlások szempontjából,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Definiáljuk az Xi véletlen változó szüleit, írjukparents(Xi), az Xi előzményeinek aminális halmaza a teljes rendezésben úgy, hogy az Xi többi előzménye feltételesen független Xi-től adottparents(Xi) esetén. Vagyis parents(Xi) ⊆{X1,…,Xi-1} úgy, hogy
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
Ha egynél több minimális halmaz létezik, bármelyik minimális halmaz választható a szülők közé. Egynél több minimális halmaz csak akkor lehet, ha az előzmények közül néhány determinisztikus függvénye a többinek.
A láncszabályt és a szülők definícióját összerakhatjuk,így
P(X1, X2,—, Xn) = ∏i=1n P(Xi|szülők(Xi)).
Az összes változóra vonatkozó P(X1, X2,—,Xn) valószínűséget nevezzük együttes valószínűségeloszlásnak. Abelief network definiáljaa közösvalószínűség-eloszlás faktorizációját, ahol a feltételes valószínűségek faktorokat alkotnak, amelyeket összeszorzunk.
A belief network, más néven Bayesiannetwork, egy aciklikusirányított gráf (DAG), ahol a csomópontok véletlen változók. Van egy ív aparents(Xi) minden eleméből Xi-be.A hiedelemhálózathoz feltételes valószínűségeloszlások halmaza tartozik – az egyes változók feltételes valószínűsége a szüleiket figyelembe véve (amely tartalmazza a szülőkkel nem rendelkező változók előzetes valószínűségeit).
Egy hiedelemhálózat tehát
- egy DAG-ból áll, ahol minden csomópontot egy véletlen változó jelöl;
- egy tartomány minden egyes véletlen változóhoz; és
- egy feltételes valószínűségi eloszlások halmaza, amely minden X változóra P(X|szülők(X)).
A hiedelemhálózat konstrukciója szerint aciklikus. Az a mód, ahogyan a lánc szabályaösszeszerkeszti a konjunkciót, megadja a sorrendet. Egy változónak csak elődei lehetnek a szülei.Különböző dekompozíciók különböző hiedelemhálózatokat eredményezhetnek.
Tegyük fel, hogy a következő változókat használjuk, amelyek mindegyike Boolean, a következő sorrendben:
- A manipuláció igaz, ha a riasztót manipulálták.
- Fire igaz, ha tűz van.
- Alarm igaz, ha megszólal a riasztó.
- Smoke igaz, ha füst van.
- Leaving igaz, ha sok ember hagyja el egyszerre az épületet.
- Report igaz, ha valaki bejelentette, hogy emberek távoznak. Report hamis, ha nincs jelentés távozásról.
A Report változó a szenzor jelentését jelöli, hogy emberek távoznak. Ez az információ megbízhatatlan, mert az ilyen jelentést adó személy lehet, hogy tréfát űz, vagy lehet, hogy senki sem figyelt oda, aki ilyen jelentést adhatott volna. Ezt a változót azért vezettük be, hogy lehetővé tegyük a megbízhatatlan szenzoradatok kondicionálását. Az ágens tudja, hogy mit jelent az érzékelő,de csak megbízhatatlan bizonyítékkal rendelkezik az épületet elhagyó emberekről.A tartomány részeként feltételezzük a következő feltételes függetlenségeket:
- A tűz feltételesen független a szabotázstól (ha nincs más információ).
- A riasztás a tűztől és a szabotázstól is függ. Ez azt jelenti, hogy nem teszünk függetlenségi feltételezéseket arról, hogy a Riasztás hogyan függ az előzményeitől e változórendezés mellett.
- A Füst csak a Tűztől függ, és feltételesen független a Szabotálástól és a Riasztástól, feltéve, hogy van-e Tűz.
- A Távozás csak a Riasztástól függ, és nem függ közvetlenül a Tűztől vagy a Szabotálástól vagy a Füsttől. Vagyis a Távozás feltételesen független a többi változótól, ha adott a Riasztás.
- A jelentés csak közvetlenül függ a Távozástól.
A 6.1. ábra hiedelemhálója fejezi ki ezeket a függőségeket.
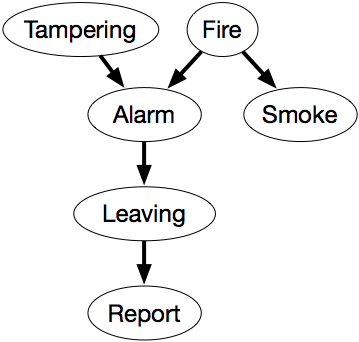
Ez a hálózat a faktorizációt
P(Tampering,Fire,Alarm,Smoke,Leaving,Report) = P(Tampering) ×P(Fire) ×P(Alarm|Tampering,Fire) ×P(Smoke|Fire) ×P(Leaving|Alarm) ×P(Report|Leaving).
Az egyes változók tartományát is meg kell határoznunk. Tegyük fel, hogy aváltozók boolék, azaz a tartományuk {igaz,hamis}. A változó kisbetűs változatát használjuk az igaz érték jelölésére, és negációt használunk a hamis értékre. Így például a Tampering=true-t tampering-nek, aTampering=false-t pedig ¬tampering-nek írjuk.
A következő példák a következő feltételes valószínűségeket feltételezik:
P(fire) = 0,01
P(alarm | fire ∧tampering) = 0.5
P(riasztás | tűz ∧¬hamisítás) = 0,99
P(riasztás | ¬tűz ∧hamisítás) = 0,85
P(riasztás | ¬tűz ∧¬hamisítás) = 0,0001
P(füst | tűz ) = 0.9
P(füst | ¬tűz ) = 0,01
P(távozás | riasztás) = 0,88
P(távozás | ¬riasztás ) = 0,001
P(jelentés | távozás ) = 0,75
P(jelentés | ¬ távozás ) = 0.01
- Minden wi vezetékre van egy Wi nevű véletlen változó a {élő,halott} tartományban, amely azt jelzi, hogy van-e áram a wi vezetékben. Wi=live azt jelenti, hogy a wi vezetékben van áram. Wi=halott azt jelenti, hogy nincs áram a wi vezetékben.
- Az Outside_power {live,dead} tartományú változó azt jelzi, hogy van-e áram az épületbe.
- Minden si kapcsoló esetében a Si_pos változó jelzi az si pozícióját. Tartománya {föl,le}.
- Minden si kapcsoló esetében a Si_st változó az si kapcsoló állapotát jelöli. Tartománya {ok,felfelé_lefelé,rövid,szaggatott,megszakított,megszakadt}. Si_st=ok azt jelenti, hogy a si kapcsoló normálisan működik. Si_st=upside_down azt jelenti, hogy a kapcsolósi fejjel lefelé van beszerelve. Si_st=rövid azt jelenti, hogy a si kapcsoló megrövidült és vezetékként működik. Si_st=breken azt jelenti, hogy a si kapcsoló elromlott, és nem engedi az áramot áramolni.
- Minden egyes megszakítócbi esetében a Cbi_st változónak {on,off} tartománya van. Cbi_st=on azt jelenti, hogy a cbi-n keresztül áram folyhat az áram, és Cbi_st=off azt jelenti, hogy a cbi-n keresztül nem folyhat az áram.
- Minden li lámpa esetében a Li_st változó a {ok,intermittent,broken} tartományban jelöli a lámpa állapotát. Li_st=ok azt jelenti, hogy a li lámpa li világítani fog, ha áram alatt van, Li_st=intermittent azt jelenti, hogy a li lámpa li időszakosan világít, ha áram alatt van, és Li_st=broken azt jelenti, hogy a li lámpa li nem működik.
Válasszunk olyan sorrendet, ahol egy változó okai a változó előtt vannak a sorrendben. Például annak változója, hogy a lámpa világít-e, a lámpa működésére és a lámpába érkező áramra vonatkozó változók után következik.
Az, hogy az l1 lámpa világít-e, csak attól függ, hogy a w0 vezetékben van-e áram, és hogy az l1 lámpa megfelelően működik-e. Más változók, mint például az s1 kapcsoló helyzete, az, hogy az l2 lámpa világít-e, vagy hogy ki Kanada királynője, lényegtelenek. Így az L1_lit szülői a W0 és az L1_st.
Nézzük a W0 változót, amely azt jelenti, hogy van-e áram a w0 vezetékben. Ha tudnánk, hogy van-e áram a w1 ésw2 vezetékekben, és ismernénk az s2 kapcsoló helyzetét, valamint azt, hogy a kapcsoló megfelelően működik-e, akkor a többi változó értéke (aL1_lit kivételével) nem befolyásolná azt a meggyőződésünket, hogy van-e áram a w0 vezetékben. Így a w0 szüleinek S2_Pos, S2_st,W1 és W2 kell lenniük.
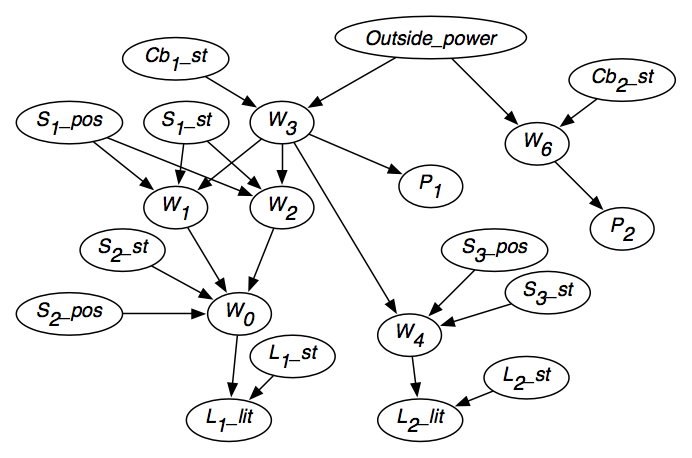
A 6.2. ábra mutatja a kapott hiedelemhálózatot, miután figyelembe vettük az egyes változók függetlenségét.A hiedelemhálózat tartalmazza a változók tartományait is, ahogyan az ábrán szerepel, és minden változó feltételes valószínűségeit a szüleihez képest.
A W1 változóra a következő feltételes valószínűségeket kell megadni:
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=élő|S1_pos=lefelé ∧S1_st=törött ∧W3=halott).
Két érték van S1_pos-ra, öt érték S1_ok-ra éskettő W3-ra, tehát 2×5×2 = 20 különböző eset van, amikor meg kell adni W1=élő értékét. Ami a valószínűségelméletet illeti, a W1 = él a 20 esetre vonatkozó valószínűség tetszőlegesen megadható. Természetesen a terület ismerete korlátozza, hogy milyen értékeknek van értelme. A W1=halott értékek kiszámíthatók a W1=élő értékekből minden egyes ilyen esetre.
Mivel az S1_st változónak nincsenek szülei, szükség van egy előzetes eloszlásra, amely megadható a valószínűségekként egy kivételével minden értékre; a fennmaradó érték levezethető abból a megkötésből, hogy minden valószínűség összege 1 legyen. Így az S1_st eloszlásának meghatározásához a következő öt valószínűségből négyet kell megadni:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
A hiedelemhálózat a feltételes függetlenség grafikus ábrázolása.A függetlenség lehetővé teszi számunkra, hogy közvetlen hatásokat ábrázoljunk a gráfon belülés előírja, hogy milyen valószínűségeket kell megadni. A hálózatból tetszőleges utólagos valószínűségek származtathatók.
A hiedelemhálózatba ágyazott függetlenségi feltételezés a következő:Minden véletlen változó feltételesen független a nem leszármazottaitól, mivel aszülői adottak. Azaz, ha X egy véletlen változó, amelynek szülei Y1,…, Yn, akkor minden olyan véletlen változó, amely nem leszármazottjaX-nek, feltételesen független X-től, adott Y1 ,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
ha R nem tartalmazza X leszármazottját. Ehhez a definícióhoz X-et önmagának leszármazottjaként vesszük fel. Ennek az egyenletnek a jobb oldala a valószínűségek formája, amelyek a hiedelemhálózat részeként vannak megadva.R bevonhatja X felmenőit és más csomópontokat, amíg azok nem X leszármazottai. A függetlenségi feltételezés azt mondja ki, hogy a nem leszármazottváltozók teljes befolyása megragadható X szüleinek értékének ismeretében.
Gyakran csak a felcímkézett DAG-ra hivatkozunk hiedelemhálózatként. Ilyenkor fontos megjegyezni, hogy minden változóhoz tartozik egy tartomány és a feltételes valószínűségi eloszlások halmaza is a hálózat része.
Az egyes változókhoz megadandó valószínűségek száma exponenciális a változó szüleinek számával.A függetlenségi feltételezés annyiban hasznos, hogy a másik változót közvetlenül befolyásoló változók száma kicsi. A változókat úgy kell rendezni, hogy a csomópontoknak a lehető legkevesebb szülője legyen.
Hithálózatok és kauzalitás
A hithálózatokat gyakran nevezik oksági hálózatoknak, és azt állítják, hogy jól reprezentálják az okságot.Emlékezzünk vissza, hogy egy oksági modell a beavatkozások eredményét jósolja meg.Tegyük fel, hogy egy terület oksági modelljét tartjuk szem előtt, ahol a területet véletlen változók egy halmazával határozzuk meg. Minden egyes X1és X2 véletlen változópárhoz, ha létezik közvetlen oksági kapcsolat X1 és X2 között (azaz az X1 megváltoztatására irányuló beavatkozás más változók bizonyos összefüggésében hatással van X2-re, és ez nem modellezhető valamilyen beavatkozó változóval), adjunk hozzá egy ívetX1 és X2 között. Azt várná, hogy az oksági modell engedelmeskedik ahiedelemhálózat függetlenségi feltételezésének. Így a hiedelemhálózat minden következtetése érvényes lenne.
Egy ilyen gráftól azt is elvárná, hogy aciklikus legyen; nem akarja, hogy valami végül önmagát okozza. Ez a feltételezés ésszerű, ha figyelembe vesszük, hogy a véletlen változók inkább bizonyos eseményeket, mint eseménytípusokat képviselnek. Vegyünk például egy oksági láncot, amely szerint “stresszesnek lenni” azt okozza, hogy “nem hatékonyan dolgozol”, ami viszont azt okozza, hogy “stresszes vagy”. A látszólagos kör megtörése érdekében a “stresszesnek lenni” különböző szakaszaiban különböző véletlen változóként ábrázolhatjuk, amelyek különböző időpontokra vonatkoznak. Ha a múltban stresszes voltál, az azt okozza, hogy jelenleg nem dolgozol jól, ami azt okozza, hogy a jövőben stresszes leszel. A változóknak meg kell felelniük az egyértelműség elvének, és jól meghatározott jelentéssel kell rendelkezniük. A változókat nem szabad eseménytípusoknak tekinteni.
A hiedelemhálózatnak önmagában nincs mondanivalója az okságról, és nem oksági függetlenséget is reprezentálhat, de különösen megfelelőnek tűnik, ha egy tartományban oksági kapcsolat van. A helyi ok-okozati összefüggéseket reprezentáló ívek hozzáadása általában kis hiedelemhálózatot eredményez. A 6.2. ábra hiedelemhálózata mutatja, hogyan lehet ezt egy egyszerű tartományban megvalósítani.
Akauzális hálózati modellek beavatkozások. Ha valaki mesterségesen kényszerítene egy változót arra, hogy egy bizonyos értéket vegyen fel, az a változó leszármazottait – de más csomópontokat nem – érintene. Végül láthatjuk, hogy a hiedelemhálózatokban az ok-okozati összefüggés hogyan kapcsolódik az 5.7. szakaszban tárgyalt oksági és bizonyító erejű érveléshez. Az oksági hiedelemhálózatot úgy tekinthetjük, mint az oksági irányú axiomatizálás távlatát. A következtetés a hiedelemhálózatokbanaz okokra való visszavezetésnek és az ezekből való előrejelzésnek felel meg. Az 5.7. szakaszban tárgyalt logikai alapú induktív szemlélet és a hiedelemhálózatok között közvetlen megfeleltetés létezik: A hiedelemhálózatok logikai programokként modellezhetők a lehetséges hipotézisek valószínűségeivel. Ezt a 14.3. szakasz ismerteti.
Megjegyezzük a “minden véletlen változó feltételesen független a nem leszármazottaitól, mivel a szülei adottak” megszorítást a hiedelemhálózatban kódolt függetlenség definíciójában. HaR tartalmazza X változó leszármazottját, a függetlenségi feltételezés nemközvetlenül alkalmazható.
Az S1_pos változónak nincsenek szülei. Így a hiedelemhálózatba ágyazott függetlenség azt határozza meg, hogy P(S1_pos=föl|A) =P(S1_pos=föl) minden olyan A-ra, amely nem érintiS1_pos leszármazottját. Ha A tartalmazza S1_pos=up leszármazottját – például,haA S2_pos=up∧L1_lit=true – a függetlenségi feltételezés nem alkalmazható közvetlenül.
Ez a hálózat többféleképpen használható:
- Azzal a tudással, hogy a kapcsolók és a megszakítók rendben vannak, valamint a külső teljesítmény és a kapcsolók helyzetének értékeivel feltételezve ez a hálózat szimulálni tudja, hogyan kellene működnie a világításnak.
- A külső áram és a kapcsolók helyzetének értékei alapján a hálózat képes következtetni bármely kimenetel valószínűségére – például arra, hogy milyen valószínű, hogy l1 világít.
- A kapcsolók értékei és az, hogy a lámpák világítanak-e, alapján következtetni lehet annak utólagos valószínűségére, hogy az egyes kapcsolók vagy megszakítók egy adott állapotban vannak.
- A hálózat néhány megfigyelés alapján visszamenőleg következtethet a kapcsolók legvalószínűbb helyzetének meghatározására.
- Megadva néhány kapcsolóhelyzetet, néhány kimenetet és néhány közbenső értéket, a hálózat felhasználható a hálózat bármely más változójának valószínűségének meghatározására.
A hiedelemhálózat egy közös valószínűségi eloszlást határoz meg, amelyből tetszőleges feltételes valószínűségek származtathatók. Egy hálózat lekérdezhetőazáltal, hogy megkérdezzük bármely változó feltételes valószínűségét bármely más változó értékétől függően. Ez tipikusan úgy történik, hogy megadjuk néhány változóra vonatkozó megfigyeléseket és lekérdezünk egy másik változót.
P(tűz) = 0,01
P(jelentés ) = 0,028
P(füst) = 0.0189
A jelentést figyelve a következőket kapjuk:
P(tűz |jelentés)= 0,2305
P(füst |jelentés) = 0,215
Várhatóan mind a manipuláció, mind a tűz valószínűségét növeli a jelentés. Mivel a tűz megnövekedett, a füst valószínűsége is megnőtt.
Tegyük fel, hogy ehelyett füstöt figyeltek meg:
P(tűz|füst) = 0,476
P(jelentés |füst) = 0,320
Megjegyezzük, hogy a manipuláció valószínűségét nem befolyásolja a füst megfigyelése; a jelentés és a tűz valószínűsége azonban megnő.
Tegyük fel, hogy mind a jelentést, mind a füstöt megfigyelték:
P(tűz |jelentés ∧füst) = 0,964
Mindkettő megfigyelése még valószínűbbé teszi a tüzet. A jelentés kontextusában azonban a füst jelenléte kevésbé valószínűvé teszi a manipulációt. Ez azért van, mert a jelentést a tűzzel magyarázzák, ami így valószínűbbé válik.
Tegyük fel ehelyett, hogy a jelentést, de nem a füstöt figyelték meg:
P(tűz|bejelentés ∧¬füst) = 0,0294
A jelentéssel összefüggésben a tűz sokkal kevésbé valószínű, és így a hamisítás valószínűsége nő a jelentés magyarázatára.
Ez a példa szemlélteti, hogy a hiedelemháló függetlenségi feltevése hogyan ad köznapi következtetéseket, és azt is bemutatja, hogy az elmagyarázás a hiedelemháló függetlenségi feltevésének következménye.
- 6.3.1 A hiedelemháló konstruálása