The StatsTest Flow: Prediction >> Continuous Dependent Variable >> More than One Independent Variable >> No Repeated Measures >> One Dependent Variable
Nem biztos, hogy ez a megfelelő statisztikai módszer? Használja a Choose Your StatsTest munkafolyamatot a megfelelő módszer kiválasztásához.
- Mi a többváltozós többszörös lineáris regresszió?
- A többváltozós többszörös lineáris regresszió feltételezései
- Linearitás
- Nincsenek kiugró értékek
- Hasonló szórás a tartományban
- A maradékok normalitása
- Nincs multikollinearitás
- Mikor használjunk többváltozós többszörös lineáris regressziót?
- Jóslás
- Folytonos függő változó
- Egynél több független változó
- Másfélváltozós többszörös lineáris regresszió példa
- Gyakran ismételt kérdések
- Segítség!
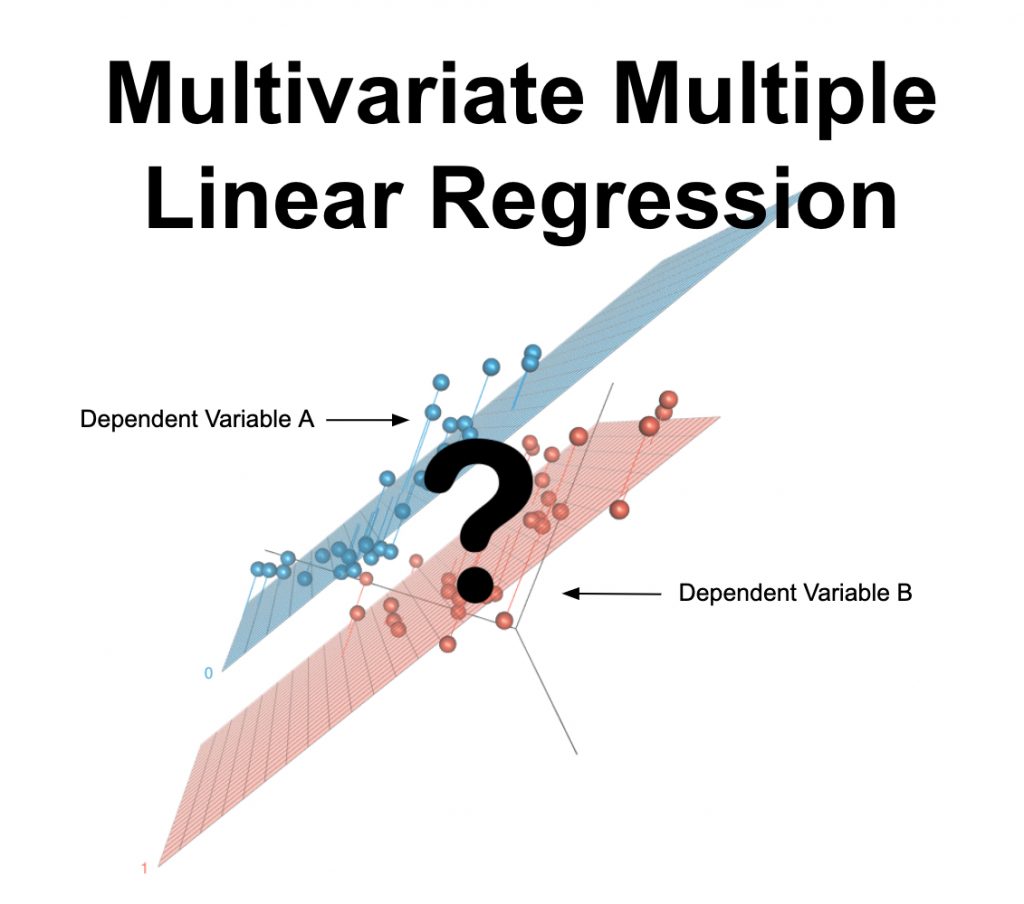
Mi a többváltozós többszörös lineáris regresszió?
A többváltozós többszörös lineáris regresszió egy olyan statisztikai teszt, amelyet több kimeneti változó előrejelzésére használnak egy vagy több másik változó segítségével. Arra is használják, hogy meghatározzák e változócsoportok és mások közötti numerikus kapcsolatot. A megjósolni kívánt változónak folytonosnak kell lennie, és az adatoknak meg kell felelniük az alább felsorolt egyéb feltételezéseknek.
A többváltozós többszörös lineáris regresszió feltételezései
Minden statisztikai módszernek vannak feltételezései. A feltételezések azt jelentik, hogy az adatoknak bizonyos tulajdonságoknak meg kell felelniük ahhoz, hogy a statisztikai módszer eredményei pontosak legyenek.
A többváltozós többszörös lineáris regresszió feltételezései a következők:
- Linearitás
- Nincsenek kiugró értékek
- Hasonló szórás a tartományon belül
- A maradékok normalitása
- Nincs multikollinearitás
Merüljünk bele ezek mindegyikébe külön-külön.
Linearitás
Azoknak a változóknak, amelyekkel foglalkozunk, lineáris kapcsolatban kell lenniük egymással. Ez azt jelenti, hogy ha a változókat ábrázolja, akkor képes lesz egy egyenes vonalat rajzolni, amely megfelel az adatok alakjának.
Nincsenek kiugró értékek
Az Önt érdeklő változók nem tartalmazhatnak kiugró értékeket. A lineáris regresszió érzékeny a kiugró értékekre, vagyis azokra az adatpontokra, amelyek szokatlanul nagy vagy kis értékekkel rendelkeznek. Azt, hogy a változók tartalmaznak-e kiugró értékeket, úgy állapíthatja meg, ha ábrázolja őket, és megfigyeli, hogy valamelyik pont messze van-e az összes többi ponttól.
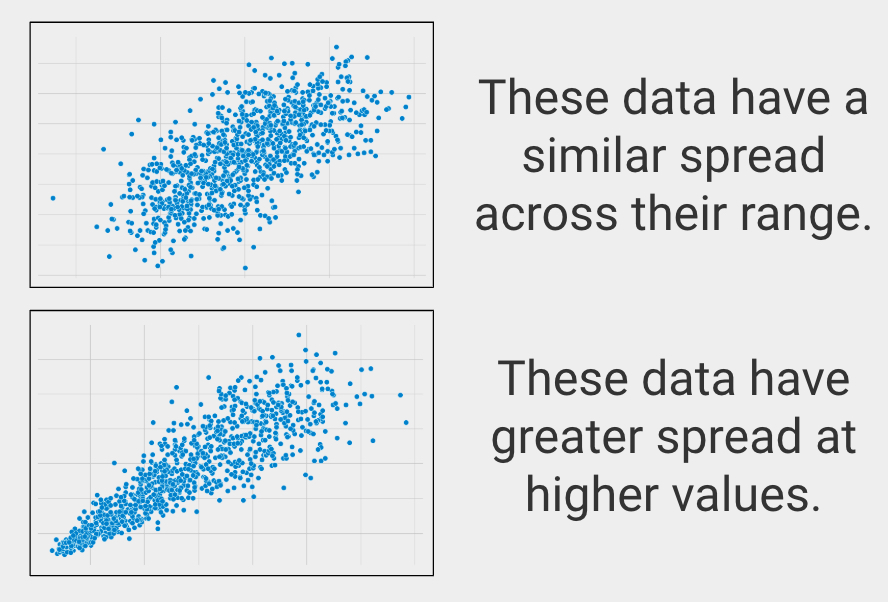
Hasonló szórás a tartományban
A statisztikában ezt homoszkedaszticitásnak nevezik, ami azt írja le, amikor a változók hasonló szórással rendelkeznek a tartományukban.
A maradékok normalitása
A maradékok szó a várható (vagy megjósolt) függő változók tényleges értékekből való kivonásából származó értékekre utal. Ezen értékek eloszlásának meg kell felelnie a normál (vagy haranggörbe) eloszlás alakjának.
Ez a feltételezés biztosítja, hogy a regresszió eredményei az adatok teljes terjedelmére egyformán alkalmazhatóak, és hogy az előrejelzésben nincs szisztematikus torzítás.
Nincs multikollinearitás
A multikollinearitás arra a forgatókönyvre utal, amikor a független változók közül kettő vagy több jelentősen korrelál egymással. Ha multikollinearitás van jelen, a regressziós együtthatók és a statisztikai szignifikancia instabillá és kevésbé megbízhatóvá válik, bár nem befolyásolja, hogy a modell önmagában mennyire jól illeszkedik az adatokhoz.
Mikor használjunk többváltozós többszörös lineáris regressziót?
A többváltozós többszörös lineáris regressziót a következő forgatókönyvek esetén érdemes használni:
- Egy változót több más változó előrejelzésében akar felhasználni, vagy a köztük lévő numerikus kapcsolatot akarja számszerűsíteni
- Az előrejelezni kívánt változók (a függő változó) folytonosak
- Egynél több független változója van, vagy egy változó, amelyet prediktorként használsz
- Nincsenek ismételt méréseid ugyanabból a megfigyelési egységből
- Egynél több függő változód van
Magyarázzuk ezeket, hogy tudd, mikor kell használni a többváltozós többszörös lineáris regressziót.
Jóslás
Egy statisztikai tesztet keres egy változó előrejelzésére egy másik változó segítségével. Ez egy előrejelzési kérdés. Más típusú elemzések közé tartozik a két változó közötti kapcsolat erősségének vizsgálata (korreláció) vagy a csoportok közötti különbségek vizsgálata (különbség).
Folytonos függő változó
A megjósolni kívánt változónak folytonosnak kell lennie. A folytonos azt jelenti, hogy az Önt érdeklő változó alapvetően bármilyen értéket felvehet, mint például a pulzusszám, a magasság, a testsúly, az 1 perc alatt megehető jégkrémek száma stb.
A NEM folytonos adattípusok közé tartoznak a rendezett adatok (például a versenyen elért helyezés, a legjobb üzleti rangsor stb.), a kategorikus adatok (nem, szemszín, faj stb.) vagy a bináris adatok (megvásárolta a terméket vagy sem, megvan a betegség vagy nincs stb.).
Ha a függő változó bináris, akkor a többszörös logisztikus regressziót, ha pedig a függő változó kategorikus, akkor a többszörös logisztikus regressziót vagy a lineáris diszkriminanciaelemzést kell használnia.
Egynél több független változó
A többváltozós többszörös lineáris regresszió akkor használható, ha minden megfigyelési egységhez egy vagy több prediktor változó több értékkel rendelkezik.
No Repeated Measures
Ez a módszer arra a forgatókönyvre alkalmas, amikor minden megfigyelési egységhez csak egy megfigyelés tartozik. A megfigyelési egység az, ami egy “adatpontot” alkot, például egy üzlet, egy vásárló, egy város stb…
Ha egy vagy több független változóval rendelkezik, de azokat ugyanazon csoportra vonatkozóan több időpontban mérik, akkor vegyes hatású modellt kell használnia.
Egynél több függő változó
A többváltozós többszörös lineáris regresszió futtatásához egynél több függő változóval kell rendelkeznie, vagy változóval, amelyet meg akar jósolni.
Ha csak egy változót jósol, akkor többszörös lineáris regressziót kell használnia.
Másfélváltozós többszörös lineáris regresszió példa
Függő változó 1: Függő változó: Bevétel
Függő változó 2: Ügyfélforgalom
Függő változó 1: Reklámra költött dollár városonként
Függő változó 2: Város lakossága
A nullhipotézis, ami statisztikai szakzsargonban azt jelenti, hogy mi történne, ha a kezelés nem csinál semmit, az, hogy nincs kapcsolat a reklámra költött dollár és a reklámdollárok vagy a városonkénti lakosságszám között. A mi tesztünk azt fogja felmérni, hogy milyen valószínűséggel igaz ez a hipotézis.
Begyűjtjük az adatainkat, és miután megbizonyosodtunk arról, hogy a lineáris regresszió feltételezései teljesülnek, elvégezzük az elemzést.
Ez az elemzés gyakorlatilag kétszeres többszörös lineáris regressziót végez mindkét függő változóval. Így amikor lefuttatjuk ezt az elemzést, béta együtthatókat és p-értékeket kapunk minden egyes kifejezésre a “bevétel” modellben és az “ügyfélforgalom” modellben. Bármely lineáris regressziós modell esetében egy béta-együtthatót kapunk, amely megegyezik a lineáris regressziós egyenes metszéspontjával (gyakran 0-val jelölve β0-ként). Ez egyszerűen az a hely, ahol a regressziós egyenes keresztezi az y-tengelyt, ha ábrázolná az adatait. Többszörös lineáris regresszió esetén ezen felül még két további béta-együttható (β1, β2 stb.) van, amelyek a független és a függő változók közötti kapcsolatot reprezentálják.
Ezek a további béta-együtthatók a változók közötti numerikus kapcsolat megértésének kulcsa. Lényegében egy adott független változó minden egyes egységnyi (1 értékű) növekedése esetén a függő változója várhatóan az adott független változóhoz tartozó béta-együttható értékével változik (miközben a többi független változót változatlanul hagyjuk).
Az ezekhez a további béta-értékekhez tartozó p-érték az az esély, hogy az eredményeinket abban a feltételezésben látjuk, hogy valójában nincs kapcsolat az adott változó és a bevétel között. A 0,05-nél kisebb vagy azzal egyenlő p-érték azt jelenti, hogy az eredményünk statisztikailag szignifikáns, és bízhatunk abban, hogy a különbség nem csupán a véletlen műve. A modellre vonatkozó általános p-érték és a változók hatását a két modell között reprezentáló egyedi p-értékek kiszámításához gyakran MANOVA-t használnak.
Ez az elemzés emellett egy R-négyzet (R2) értéket is eredményez. Ez az érték 0-1 között mozoghat, és azt mutatja meg, hogy a lineáris regressziós egyenes mennyire jól illeszkedik az adatpontokhoz. Minél magasabb az R2, annál jobban illeszkedik a modellje az adatokhoz.
Gyakran ismételt kérdések
K: Mi a különbség a többváltozós többszörös lineáris regresszió és a lineáris regresszió többszöri futtatása között?
A: Fogalmilag hasonlóak, mivel az egyes modell együtthatói mindkét esetben azonosak lesznek. Lényeges különbség azonban, hogy a többváltozós lineáris regresszió szignifikanciatesztjei és konfidenciaintervallumai figyelembe veszik a több függő változót.
K: Hogyan futtassak többváltozós többszörös lineáris regressziót SPSS, R, SAS vagy STATA programban?
A: Ez az erőforrás arra összpontosít, hogy minden alkalommal segítsen a megfelelő statisztikai módszer kiválasztásában. Számos forrás áll rendelkezésre, hogy segítsen kitalálni, hogyan futtassa ezt a módszert az adataival:
R cikk: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/
Segítség!
Ha még mindig nem tudsz rájönni valamire, fordulj bátran hozzánk.