Tetraéder

Az oldal tartalma Mi az a tetraéder? A tetraéder darabjai Tetraéder számok Tetraéder a kockában Tetraéderek gyűrűi Tetraéderek az Interneten

A “Mathematische Basteleien”

Mi a tetraéder?

A tetraéder olyan háromdimenziós alakzat, amelynek négy egyenlő háromszöge van. Ha három három háromszöget felemelünk (1), akkor a tetraédert kapjuk felülnézetben (2). Általában perspektivikusan ábrázolják (3).

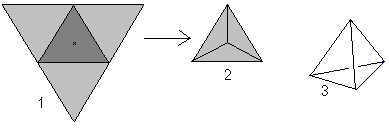
Ha megnézzük a tetraéder szót (a tetraéder azt jelenti: “négy síkkal”), akkor minden olyan piramist, amelynek alapja egy háromszög, tetraédernek nevezhetünk.

Mindenesetre a tetraéder az egyenes, szabályos háromszögpiramis ezen a honlapon.

A tetraéder tetejének darabjai
Egy oldalsó háromszög magassága és területe
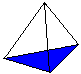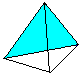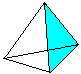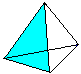
Négy egyenlő oldalú háromszög alkot egy tetraédert.

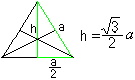…	Egy háromszöget választunk ki: A három magasság egy pontban metszi egymást, mint minden háromszögben. Ez a háromszög középpontja. A magasság kiszámítható az a oldal alapján, mint h=sqr(3)/2*a a Pitagorasz-tétel segítségével.

A magasságok szintén középértékek, és 2:1 arányban metszik egymást. Ezt használjuk a következő számításokban.

A háromszög területe A=sqr(3)/4*a².

Térmagasság

A tetraéder magassága az alapháromszög középpontja (1) és a csúcs (2) között van. A számításokhoz figyelembe veszi az úgynevezett támaszháromszöget (3, sárga), amelyetegy él és két háromszög magassága alkot. A Pitagorasz-tétel segítségével H=sqr(6)/3*a.
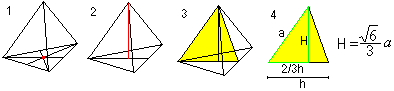
Középpont, körülírt gömb és beírt gömb A tetraéder középpontja két térmagasság (1,2,3) metszéspontja. Ez a súlypont, a négy sarkon keresztül a gömb középpontja, és a legnagyobb gömb középpontja, amely még befér a tetraéder belsejébe (4).

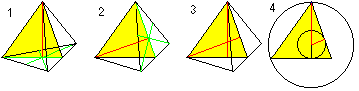
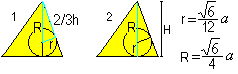…	Két képletet kapunk r-re és R-re aPythagorasz-tétel (1) és H=R+r (2) segítségével: Ez r=sqr(6)/12*a , R=sqr(6)/4*a.

Szögfelület

….…..

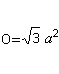Az alap és az oldalfelületek területe alkotja aO felületet. Van O=4*A (háromszög) = sqr(3)a².

Térfogat

Tetraéder számok teteje

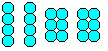…….	Ha 20 golyót két négyes és két hatos csoportba ragasztunk, akkor egy jól ismert rejtvényt kapunk: Négy darabból kell piramist alkotni.

Sok hasonló rejtvény van.

Tetraéder a kocka tetején
A kocka hat átlós oldala tetraédert alkot a kockában.
Ha ismered a 3D-s nézetet, akkor háromdimenziósan megnézheted a következő két kockapárt.

A tetraéder térfogata a kocka térfogatának harmadrészét teszi ki.

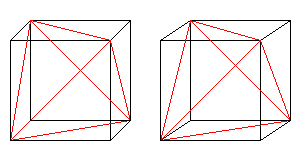
Ha rajzolunk egy második tetraédert és a metszésvonalakat,akkor két tetraéder áthatását kapjuk.

Az ábra az eredeti kocka oldalátlóiból és az oldalnégyzetek középpontjainak összekötő vonalaiból áll. Az utolsók egy oktaédert alkotnak.

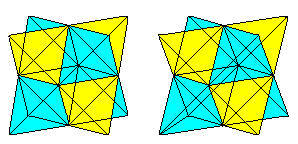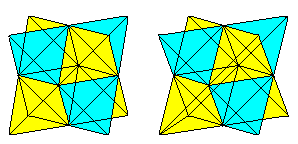
Tetraéderek gyűrűi tetején
Papír tetraédereket készíthetsz, és páros számmal ragaszthatsz belőlük egy gyűrűt. A gyűrű a közepén keresztül folyamatosan befelé vagy kifelé csavarodhat. Ez egy szép játék. – Ezeket a gyűrűket kaleidociklusoknak is nevezik.többet találsz a Kaleidociklusok című weboldalamon.

Tetraéderek az Internettop

Német

Christof Weber
Washat ez Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

English

Eric W. Weisstein (World of Mathematics)
Tetraéder

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraéder

Joyce Frost és Peg Cagle (mathforum)
AnAmazing, Space Filling, Non-regular Tetrahedron

Wikipedia
Tetraéder,Tetrapod(structure), Tetrahedralnumber