By Evan Ma

(Matematika és fizika oktató a The Edge Learning Centerben)

A logaritmikus függvény úgy tűnik, sok diákot összezavar az IB Math SL programban tanuló diákok közül. Ahhoz, hogy megfelelően megértsük, definiáljuk

ahol , egy szigorúan pozitív valós számot nevezünk bázisnak, pedig a hatvány. Például a következőket mindannyian kívülről tudjuk:

és így tovább. A logaritmusfüggvény ezt fordítva csinálja – egy számot argumentumként megadva a hatványt adja ki egy megadott bázis függvényében, ezért a következőképpen definiálódik.

Ha

akkor

Ezért világos, hogy

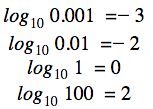
és így tovább. Nézzünk további példákat más bázisok bevonásával:

Töltsük ki gyakorlatként a következő kérdéseket: (a) , (b) , (c) , (d) . A válaszok a blog végén találhatók.

A logaritmus definíciójából azt is láthatjuk, hogy ha egy valós szám bázisát a bázis-logaritmussal emeljük, akkor a számot kapjuk vissza, vagyis

Ezt megpróbálhatod ellenőrizni a számológépeddel különböző érvényes bázisok esetén. Ez az azonosság fontos, amikor logaritmikus egyenleteket próbálunk megoldani, amire példákat adunk majd alter.

Most nézzük meg a logaritmus szabályait. A logaritmus definíciójához hasonlóan az indexek törvényeit használjuk a szabályok levezetéséhez:

1. A szorzat logaritmusa a logaritmusok összege

Bizonyítás: Mondjuk és , tehát

2. Mr alap logaritmusa szorozva

Bizonyíték: Mondjuk , tehát

3. Egy hányados logaritmusa a logaritmusok különbsége

Bizonyíték: Mondjuk és , tehát

4. Az utolsó szabályt alapváltozási formulának nevezzük. A képlet levezetéséhez egy példát fogunk segítségül hívni. Tegyük fel, hogy tudni akarjuk, milyen hatványra kell emelni 2-t ahhoz, hogy 50-et kapjunk. Mivel 50 nem a 2 egész számú hatványa, a válasz nem túl egyértelmű. Ezért azt írjuk, hogy

és ezért. Ahhoz, hogy megtaláljuk , mondjuk, 10-es bázisú logaritmust alkalmazunk az egyenlet mindkét oldalára, mivel a számológépünkön nem biztos, hogy van 2-es bázisú logaritmus billentyű:

Az értéke 4 szignifikáns számjegyre korrigálva körülbelül 5,644. Valójában ellenőrizheted a válaszodat, ha 2-t 5,644 hatványára emeled, és láthatod, hogy a válasz körülbelül 50.

A probléma általánosításához tegyük fel, hogy olyan értéket kell találnunk, hogy és bázis logaritmus nem áll rendelkezésünkre, ezért ehelyett használhatunk bázis- logaritmust a

egyenlet szerint, és így

Egy példával élve, tekintsük a következőt. Tegyük fel, hogy egy 10 000 dolláros összeget letétbe helyezünk évi 2,5%-os kamat mellett, évente kamatoztatva. Mennyi ideig kell a pénzt a számlán tartani ahhoz, hogy 50 000 dollárra nőjön?

A kérdés megválaszolásához alapvetően olyan n-t próbálunk találni, hogy

Mivel az egyszerű tudományos számológépem nem teszi lehetővé, hogy 1 bázist adjak meg.025 a logaritmuskulcshoz, a bázisváltási képletre kell hagyatkoznom, és a 10-es bázist kell használnom, és így

Mivel a kamatot évente kamatoztatjuk, 66 év alatt legalább ötszörösére nő.

A logaritmusok szabályainak felfedezése után bevezetjük a természetes logaritmus függvényt, vagy . Ez alap-, ahol a jeles irracionális szám ≈2,71828, és amelynek jelentőségét a tudományokban és a matematikában nem lehet eléggé hangsúlyozni. A bázis-logaritmust tehát a következőképpen definiáljuk:

Ha

akkor

A következőkben nézzünk meg két példát, ahol a logaritmusegyenletek megoldása során gyakori hibákat követnek el. Próbáld ki, hogy be tudod-e azonosítani a hibát.

Hol van a hiba? Nézd meg közelebbről! Természetesen a második lépésben nem lehet a logaritmust az összeadás jelén keresztül “szétválasztani”. Ne feledd, egy logaritmust csak akkor tudsz összegre “osztani”, ha a logaritmust egy szorzatra alkalmazod, nem pedig egy összegre. A helyes lépések tehát a következők:

Most nézzük meg a következő példát, hátha be tudod azonosítani a hibát:

Hol van a hiba? Igen, a második lépésben – logaritmusok hányadosa természetesen nem a hányados logaritmusa. Inkább az alapváltozási képletet használhatjuk az első lépés egyszerűsítésére, a következőképpen:

Végezetül bemutatjuk, hogyan használhatjuk a logaritmus szabályait a következők megoldására:

Figyelhetjük, hogy az ismeretlen a logaritmus argumentumában bázisként és változóként is szerepel. Hogyan tudjuk megoldani a értékét? A módszer továbbra is a logaritmus szabályainak következetes alkalmazásán múlik. Először is, mindkét oldalt a bázis hatványaként emeljük, és így

Emlékezhetünk a logaritmus definíciójából, hogy a baloldal egyszerűen a logaritmus argumentumává válik, és ezért

A fenti egyenlet átrendezésével meg kell oldanunk

Megjegyezve, hogy ez hasonlít egy -os kvadrátra, a következőképpen oldjuk meg -et:

Most, hol van a negatív gyök? Mivel egyben a logaritmus bázisa is, ezért a negatív gyök mint megoldás elvetendő. Ezért a végső válasz.

A fenti példák áttekintésével láthatjuk, hogy egy látszólag nehéz logaritmikus egyenlet megoldása egyáltalán nem nehéz – elég csak következetesen alkalmazni a logaritmus szabályait, és máris megkapjuk a helyes megoldást.

Válaszok a kérdésekre: (a) 2 (b) 3 (c) -3 (d) -2.