Grafi in Python

Origini della teoria dei grafi

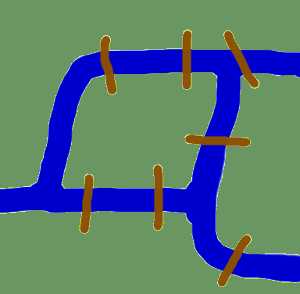Prima di iniziare con le implementazioni reali dei grafi in Python e prima di iniziare con l’introduzione dei moduli Python che trattano i grafi, vogliamo dedicarci alle origini della teoria dei grafi.
Le origini ci portano indietro nel tempo alla Künigsberg del XVIII secolo. Allora Königsberg era una città della Prussia. Il fiume Pregel scorreva attraverso la città, creando due isole. La città e le isole erano collegate da sette ponti come mostrato. Gli abitanti della città erano mossi dalla domanda, se era possibile fare una passeggiata attraverso la città visitando ogni zona della città e attraversando ogni ponte solo una volta? Ogni ponte deve essere attraversato completamente, cioè non è permesso camminare a metà strada su un ponte e poi girarsi e successivamente attraversare l’altra metà dall’altro lato. Non è necessario che la passeggiata inizi e finisca nello stesso punto.Leonhard Euler ha risolto il problema nel 1735 dimostrando che non è possibile. Scoprì che la scelta di un percorso all’interno di ogni territorio è irrilevante e che l’unica cosa che conta è l’ordine (o la sequenza) in cui i ponti vengono attraversati. Aveva formulato un’astrazione del problema, eliminando i fatti non necessari e concentrandosi sulle aree di terra e sui ponti che le collegano. In questo modo creò le basi della teoria dei grafi. Se vediamo un “territorio” come un vertice e ogni ponte come un bordo, abbiamo “ridotto” il problema a un grafo.

Introduzione alla teoria dei grafi con Python

Prima di iniziare il nostro trattato sulle possibili rappresentazioni Python dei grafi, vogliamo presentare alcune definizioni generali di grafi e dei suoi componenti.
Un “grafo “1 in matematica e informatica consiste di “nodi”, conosciuti anche come “vertici”.I nodi possono essere collegati o meno tra loro. Nella nostra illustrazione – che è una rappresentazione pittorica di un grafo – il nodo “a” è collegato con il nodo “c”, ma “a” non è collegato con “b”. La linea di collegamento tra due nodi è chiamata bordo. Se i bordi tra i nodi sono indiretti, il grafo è chiamato grafo indiretto. Se un bordo è diretto da un vertice (nodo) ad un altro, un grafico è chiamato un grafico diretto. Un bordo diretto è chiamato arco.
Anche se i grafi possono sembrare molto teorici, molti problemi pratici possono essere rappresentati da grafi. Sono spesso usati per modellare problemi o situazioni in fisica, biologia, psicologia e soprattutto in informatica. In informatica, i grafi sono usati per rappresentare le reti di comunicazione, l’organizzazione dei dati, i dispositivi di calcolo, il flusso di calcolo,

In quest’ultimo caso, sono usati per rappresentare l’organizzazione dei dati, come il file system di un sistema operativo, o le reti di comunicazione. Anche la struttura dei link dei siti web può essere vista come un grafo, cioè un grafo diretto, perché un link è un bordo diretto o un arco.
Python non ha un tipo di dati o una classe incorporata per i grafi, ma è facile implementarli in Python. Un tipo di dati è ideale per rappresentare i grafi in Python, cioè i dizionari. Il grafico nella nostra illustrazione può essere implementato nel modo seguente:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Le chiavi del dizionario sopra sono i nodi del nostro grafico. I valori corrispondenti sono liste con i nodi, che sono collegati da un bordo. Non c’è un modo più semplice ed elegante di rappresentare un grafo.
Un bordo può essere visto come una 2-tupla con i nodi come elementi, cioè (“a”, “b”)
Funzione per generare la lista di tutti i bordi:Questo codice genera il seguente output, se combinato con il dizionario del grafo precedentemente definito:

 $ python3 graph_simple.py 

Come possiamo vedere, non c’è nessun bordo contenente il nodo “f”. “f” è un nodo isolato del nostro grafico.
La seguente funzione Python calcola i nodi isolati di un dato grafico:Se chiamiamo questa funzione con il nostro grafico, verrà restituita una lista contenente “f”:

Graphs come classe Python

Prima di continuare a scrivere funzioni per i grafi, facciamo un primo tentativo di implementazione di una classe di grafi Python. Se guardate il seguente elenco della nostra classe, potete vedere nel metodo __init__ che usiamo un dizionario “self.__graph_dict” per memorizzare i vertici e i loro corrispondenti vertici adiacenti.
Se avviate questo modulo standalone, otterrete il seguente risultato:

Percorsi nei grafi

Ora vogliamo trovare il percorso più breve da un nodo ad un altro nodo. Prima di arrivare al codice Python per questo problema, dobbiamo presentare alcune definizioni formali.
Viti adiacenti:
Due vertici sono adiacenti quando sono entrambi incidenti su un bordo comune.
Percorso in un grafo indiretto:
Un percorso in un grafo indiretto è una sequenza di vertici P = ( v1, v2, …, vn ) ∈ V x V x … x V tale che vi è adiacente a v{i+1} per 1 ≤ i < n. Un tale percorso P è chiamato percorso di lunghezza n da v1 a vn.
Percorso semplice:
Un percorso senza vertici ripetuti è chiamato percorso semplice.
esempio:
(a, c, e) è un percorso semplice nel nostro grafico, così come (a,c,e,b). (a,c,e,b,c,d) è un percorso ma non un percorso semplice, perché il nodo c appare due volte.

Il seguente metodo trova un percorso da un vertice iniziale a un vertice finale:Se salviamo la nostra classe di grafi che include il metodo find_path come “graphs.py”, possiamo controllare il modo di lavorare della nostra funzione find_path:Il risultato del programma precedente appare così:
Il metodo find_all_paths trova tutti i percorsi tra un vertice iniziale e un vertice finale:Abbiamo cambiato leggermente il nostro grafico di esempio aggiungendo i bordi da “a” a “f” e da “f” a “d” per testare il metodo precedentemente definito:Il risultato appare così:

Degree

Il grado di un vertice v in un grafico è il numero di bordi che lo collegano, con i loop contati due volte. Il grado di un vertice v è indicato con deg(v). Il grado massimo di un grafo G, indicato con Δ(G), e il grado minimo di un grafo, indicato con δ(G), sono il grado massimo e minimo dei suoi vertici.
Nel grafico a destra, il grado massimo è 5 nel vertice c e il grado minimo è 0, cioè il vertice isolato f.
Se tutti i gradi di un grafo sono uguali, il grafo è un grafo regolare.In un grafo regolare, tutti i gradi sono uguali, e quindi possiamo parlare di grado del grafo.
La formula della somma dei gradi (Handshaking lemma):
∑v &in; Vdeg(v) = 2 |E|
Questo significa che la somma dei gradi di tutti i vertici è uguale al numero dei bordi moltiplicato per 2.Possiamo concludere che il numero di vertici con grado dispari deve essere pari. Questa affermazione è nota come lemma di handshaking. Il nome “lemma della stretta di mano” deriva da un popolare problema matematico: in qualsiasi gruppo di persone il numero di persone che hanno stretto la mano ad un numero dispari di altre persone del gruppo è pari.
Il seguente metodo calcola il grado di un vertice:
Il seguente metodo calcola una lista contenente i vertici isolati di un grafico:I metodi delta e Delta possono essere usati per calcolare rispettivamente il grado minimo e massimo di un vertice:

La sequenza di gradi

La sequenza di gradi di un grafo indiretto è definita come la sequenza dei gradi dei suoi vertici in un ordine non crescente.
Il seguente metodo restituisce una tupla con la sequenza di gradi del grafico di istanza:
La sequenza di gradi del nostro grafo di esempio è la seguente sequenza di interi: (5,2,1,1,1,0).
I grafi isomorfi hanno la stessa sequenza di gradi. Tuttavia, due grafi con la stessa sequenza di gradi non sono necessariamente isomorfi.
C’è la questione se una data sequenza di gradi può essere realizzata da un grafo semplice. Il teorema di Erdös-Gallai afferma che una sequenza non crescente di n numeri di (fori = 1, …, n) è la sequenza di grado di un grafo semplice se e solo se la somma della sequenza è pari e la seguente condizione è soddisfatta:

Implementazione del teorema di Erdös-Gallai

La nostra classe di grafi – vedi sotto per un elenco completo – contiene un metodo “erdoes_gallai” che decide se una sequenza soddisfa il teorema di Erdös-Gallai. Per prima cosa si controlla se la somma degli elementi della sequenza è dispari. Se è così la funzione restituisce False, perché il teorema di Erdös-Gallai non può più essere soddisfatto. Dopo questo controlliamo con il metodo statico is_degree_sequence se la sequenza di input è una sequenza di grado, cioè che gli elementi della sequenza non sono crescenti. Questo è un po’ superfluo, dato che si suppone che l’input sia una sequenza di gradi, quindi potete abbandonare questo controllo per efficienza. Ora, controlliamo nel corpo della seconda istruzione if, se la disequazione del teorema è soddisfatta:
Versione senza il test superfluo della sequenza di gradi:

Densità del grafico

La densità del grafico è definita come il rapporto tra il numero di bordi di un dato grafico e il numero totale di bordi che il grafico potrebbe avere. In altre parole: Misura quanto un dato grafo è vicino ad un grafo completo.
La densità massima è 1, se un grafico è completo. Questo è chiaro, perché il numero massimo di bordi in un grafico dipende dai vertici e può essere calcolato come:
max. numero di bordi = ½ * |V| * ( |V| – 1 ).
D’altra parte la densità minima è 0, se il grafo non ha bordi, cioè è un grafo isolato.
Per i grafi semplici indiretti, la densità del grafo è definita come: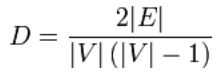

Un grafo denso è un grafo in cui il numero di bordi è vicino al numero massimo di bordi. Un grafo con pochi bordi è chiamato grafo rado. La definizione di questi due termini non è molto precisa, cioè non c’è un limite superiore minimo (supremo) per una densità rada e un limite inferiore massimo (infimo) per definire un grafo denso.
La notazione matematica più precisa usa la notazione big O:
Grafo rado:
Grafo denso:
Un grafo denso è un grafo G = (V, E) in cui |E| = Θ(|V|2).
“density” è un metodo della nostra classe per calcolare la densità di un grafo:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Possiamo provare questo metodo con il seguente script. Un grafo completo ha una densità di 1 e un grafo isolato ha una densità di 0, come possiamo vedere dai risultati dello script di prova precedente:

$ python test_density.py 0.4666666666671.00.0

Grafi connessi

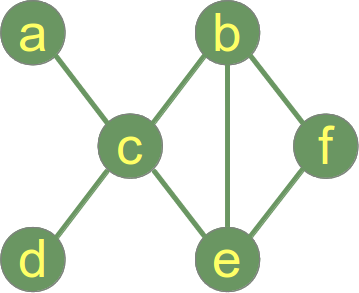Un grafico si dice connesso se ogni coppia di vertici nel grafico è connessa. L’esempio di grafo a destra è un grafo connesso.

È possibile determinare con un semplice algoritmo se un grafo è connesso:

1. Scegliere un nodo arbitrario x del grafico G come punto di partenza
2. Determinare l’insieme A di tutti i nodi che possono essere raggiunti da x.
3. Se A è uguale all’insieme dei nodi di G, il grafo è connesso; altrimenti è disconnesso.

Impieghiamo un metodo is_connected per controllare se un grafo è un grafo connesso. Non poniamo l’accento sull’efficienza ma sulla leggibilità.
Se si aggiunge questo metodo alla nostra classe grafo, possiamo testarlo con il seguente script. Supponendo di salvare la classe graph come graph2.py:
Un componente connesso è un massimo sottografo connesso di G. Ogni vertice appartiene esattamente ad un componente connesso, così come ogni bordo.

Distanza e diametro di un grafico

La distanza “dist” tra due vertici in un grafico è la lunghezza del percorso più breve tra questi vertici. Per il calcolo di una distanza non sono ammessi backtracks, deviazioni o loop.
Nel nostro grafico di esempio sulla destra, la distanza tra il vertice a e il vertice f è 3, cioè dist(a,f) = 3, perché la via più breve è attraverso i vertici c ed e (o c e b alternativamente).
L’eccentricità di un vertice s di un grafico g è la massima distanza da ogni altro vertice del grafico:
e(s) = max( { dist(s,v) | v ∈ V })
(V è l’insieme di tutti i vertici di g)
Il diametro d di un grafico è definito come la massima eccentricità di qualsiasi vertice del grafico. Ciò significa che il diametro è la lunghezza del percorso più breve tra i nodi più distanti. Per determinare il diametro di un grafo, trova prima il percorso più breve tra ogni coppia di vertici. La lunghezza maggiore di uno qualsiasi di questi percorsi è il diametro del grafo.
Possiamo vedere direttamente nel nostro grafico di esempio che il diametro è 3, perché la lunghezza minima tra a e f è 3 e non c’è un’altra coppia di vertici con un percorso più lungo.
Il metodo seguente implementa un algoritmo per calcolare il diametro. Possiamo calcolare il diametro del nostro grafo di esempio con il seguente script, assumendo di nuovo che la nostra classe completa di grafi sia salvata come graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Stamperà il valore 3.

La classe completa di grafi Python

Nel seguente codice Python, trovate il modulo completo della classe Python con tutti i metodi discussi:graph2.py

Albero / Foresta

Un albero è un grafico indiretto che non contiene cicli. Questo significa che ogni due vertici del grafico sono collegati esattamente da un percorso semplice.
Una foresta è un’unione disgiunta di alberi. Contrariamente alle foreste in natura, una foresta nella teoria dei grafi può consistere in un singolo albero!
Un grafo con un vertice e nessun bordo è un albero (e una foresta).
Un esempio di albero: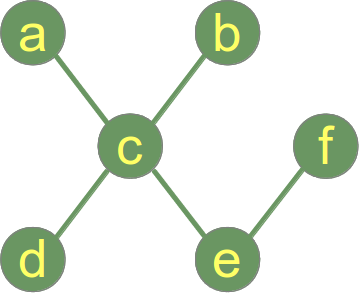

Mentre l’esempio precedente raffigura un grafo che è un albero e una foresta, l’immagine seguente mostra un grafo che consiste di due alberi, cioè il grafo è una foresta ma non un albero.cioè il grafo è una foresta ma non un albero:

Panoramica delle foreste:

Con un vertice:

Grafi di foresta con due vertici:

Grafi di foresta con tre vertici:

Albero di spanning

Un albero di spanning T di un grafo connesso e indiretto G è un sottografo G’ di G, che è un albero, e G’ contiene tutti i vertici e un sottoinsieme dei bordi di G. G’ contiene tutti i bordi di G, se G è un grafico ad albero. Informalmente, un albero di spanning di G è una selezione di bordi di G che formano un albero che attraversa ogni vertice. Cioè, ogni vertice si trova nell’albero, ma non sono contenuti cicli (o loop).
Esempio:
Un grafo completamente connesso: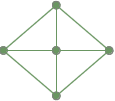

Due alberi di spanning dal precedente grafo completamente connesso: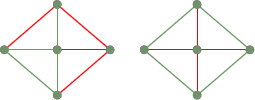

Gioco Hamiltoniano

Un percorso Hamiltoniano è un percorso in un grafico indiretto o diretto che visita ogni vertice esattamente una volta. Un ciclo hamiltoniano (o circuito) è un percorso hamiltoniano che è un ciclo.
Nota per gli informatici: Generalmente, non è possibile determinare se tali percorsi o cicli esistono in grafi arbitrari, perché è stato dimostrato che il problema del percorso hamiltoniano è NP-completo.
Prende il nome da William Rowan Hamilton che ha inventato il cosiddetto “gioco icosiano”, o puzzle di Hamilton, che consiste nel trovare un ciclo hamiltoniano nel grafico dei bordi del dodecaedro. Hamilton ha risolto questo problema usando il calcolo icosiano, una struttura algebrica basata su radici di unità con molte somiglianze con i quaternioni, che ha anche inventato.

Elenco completo della classe Graph

Possiamo testare questa classe Graph con il seguente programma:Se avviamo questo programma, otteniamo il seguente output:
Note:
1 I grafi studiati nella teoria dei grafi (e in questo capitolo del nostro tutorial Python) non devono essere confusi con i grafi delle funzioni
2 Un singleton è un insieme che contiene esattamente un elemento.
Crediti:
Narayana Chikkam, nchikkam(at)gmail(dot)com, ha evidenziato un errore di indice nel metodo “erdoes_gallai”. Grazie mille, Narayana!