Di Evan Ma

(tutor di matematica e fisica al The Edge Learning Center)

La funzione logaritmica sembra confondere molti studenti che studiano il programma IB Math SL. Per capirla bene, definiamo

dove , un numero reale strettamente positivo, è chiamato base e è la potenza. Per esempio, conosciamo tutti a memoria la seguente:

e così via. La funzione logaritmica lo fa al contrario – dato un numero come argomento, fornisce la potenza soggetta a una base specificata, e quindi è definita come segue.

Se

allora

Quindi è chiaro che

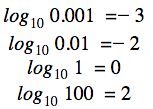
e così via. Guardiamo altri esempi che coinvolgono altre basi:

Completiamo le seguenti domande come esercizio: (a) , (b) , (c) , (d) . Le risposte si trovano alla fine di questo blog.

Dalla definizione di logaritmo, possiamo anche vedere che se eleviamo la base per il logaritmo base di un numero reale , riavremo il numero , viz

Puoi provare a verificare questo usando la tua calcolatrice per diverse basi valide. Questa identità è importante quando cerchiamo di risolvere equazioni logaritmiche, esempi delle quali saranno dati in seguito.

Ora, diamo un’occhiata alle regole del logaritmo. Simile alla definizione del logaritmo, usiamo le leggi degli indici per derivare le regole:

1. Il logaritmo di un prodotto è la somma dei logaritmi

Prova: Diciamo e , quindi

2. Il logaritmo in base di Mr è volte

Prova: Diciamo , quindi

3. Il logaritmo di un quoziente è la differenza dei logaritmi

Prova: Diciamo e , quindi

4. La regola finale si chiama formula del cambiamento di base. Useremo un esempio come strumento per ricavare la formula. Diciamo che vogliamo sapere quale potenza deve essere elevata a 2 per ottenere 50. Poiché 50 non è una potenza intera di 2, la risposta non è molto ovvia. Quindi, scriviamo

e quindi. Per trovare , diciamo che applichiamo il logaritmo in base 10 a entrambi i lati dell’equazione, poiché la nostra calcolatrice potrebbe non avere il tasto del logaritmo in base 2:

Corretto a 4 cifre significative, il valore di è circa 5,644. Infatti, puoi verificare la tua risposta elevando 2 alla potenza di 5,644 per vedere che la risposta è circa 50.

Per generalizzare il problema, diciamo che dobbiamo trovare tale che e il logaritmo base- non è a nostra disposizione, possiamo quindi usare invece il logaritmo base secondo l’equazione

e quindi

A titolo di esempio, consideriamo quanto segue. Supponiamo che una somma di 10.000 dollari sia depositata ad un interesse del 2,5% annuo, composto annualmente. Per quanto tempo il denaro deve essere tenuto sul conto perché cresca fino a 50.000 dollari?

Per rispondere alla domanda, stiamo fondamentalmente cercando di trovare n tale che

Come la mia semplice calcolatrice scientifica non mi permette di specificare una base di 1.025 per la chiave logaritmica, dovrò affidarmi alla formula del cambio di base e usare la base-10, e quindi

Siccome l’interesse è composto annualmente, ci vorranno 66 anni per crescere almeno 5 volte.

Avendo esplorato le regole dei logaritmi, introduciamo la funzione logaritmica naturale, o . È base-, dove è l’eminente numero irrazionale ≈2.71828 e la cui importanza nelle scienze e nella matematica non sarà mai sottolineata abbastanza. Quindi, il logaritmo in base è definito come segue.

Se

allora

In seguito, diamo un’occhiata a due esempi in cui vengono fatti errori comuni nella risoluzione delle equazioni dei logaritmi. Vedi se riesci a identificare l’errore.

Dove si trova l’errore? Guarda meglio. Naturalmente, nel secondo passo, non si può “dividere” il logaritmo attraverso il segno di addizione. Ricordate, potete “dividere” un logaritmo in una somma solo se il logaritmo è applicato a un prodotto, non a una somma. I passi corretti sono quindi i seguenti:

Ora, guardiamo il seguente esempio, e vediamo se riesci a identificare l’errore:

Dove è l’errore? Sì, è nel secondo passo – un quoziente di logaritmi non è ovviamente il logaritmo del quoziente. Piuttosto, possiamo usare la formula del cambio di base per semplificare il primo passo, come segue:

Infine, illustreremo come usare le regole del logaritmo per risolvere il seguente:

Si può notare che l’incognita appare come base e variabile nell’argomento del logaritmo. Come possiamo risolvere ? Il metodo dipende ancora dall’applicazione coerente delle regole del logaritmo. Per prima cosa, eleviamo entrambi i lati come potenze della base , e quindi

Si ricorda dalla definizione di logaritmo che il lato sinistro diventerà semplicemente l’argomento del logaritmo, e quindi

Ristrutturando l’equazione di cui sopra, dobbiamo risolvere

Notando che questo assomiglia a una quadratica in , risolviamo come segue:

Ora, dov’è la radice negativa? Poiché è anche la base del logaritmo, la radice negativa è quindi scartata come soluzione. Quindi, è la risposta finale.

Ripercorrendo gli esempi precedenti, si può vedere che risolvere un’equazione logaritmica apparentemente difficile non è affatto difficile – basta applicare le regole del logaritmo in modo coerente e si può ottenere la soluzione corretta.

Risposte alle domande: (a) 2 (b) 3 (c) -3 (d) -2.

.