6.3 Reti di credenze

La nozione di indipendenza condizionata può essere usata per dare una rappresentazione concisa di molti domini. L’idea è che, data una variabile casuale X, può esistere un piccolo insieme di variabili che influenzano direttamente il valore della variabile nel senso che X è incondizionatamente indipendente da altre variabili dati i valori delle variabili che influenzano direttamente. L’insieme delle variabili che influenzano localmente è chiamato coperta di Markov. Questa località è ciò che viene sfruttata in una rete di credenze. Una rete di credenze è un modello diretto di dipendenza condizionale tra un insieme di variabili casuali. L’affermazione precisa dell’indipendenza condizionata in una rete di credenza tiene conto della direzionalità.

Per definire una rete di credenza, iniziamo con un insieme di variabili casuali che rappresentano tutte le caratteristiche del modello. Supponiamo che queste variabili siano {X1,…,Xn}.Successivamente, selezionare un ordinamento totale delle variabili, X1,…,Xn.

La regola della catena (Proposizione 6.3) mostra come decomporre una congiunzione in probabilità condizionali:

P(X1=v1∧X2=v2∧—∧Xn=vn)
	=	∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).

Ovvero, in termini di variabili casuali e distribuzioni di probabilità,

P(X1, X2,—, Xn)

=

∏i=1n P(Xi|X1, —, Xi-1).

Definire i genitori della variabile casuale Xi, scrittoparents(Xi), come un insieme minimo di predecessori di Xi nell’ordinamento totale tale che gli altri predecessori di Xi siano condizionatamente indipendenti da Xi datoparents(Xi). Cioè, genitori(Xi) ⊆{X1,…,Xi-1} tale che

P(Xi|Xi-1…X1) = P(Xi|genitori(Xi)).

Se esiste più di un insieme minimo, qualsiasi insieme minimo può essere scelto come genitori. Ci può essere più di un insieme minimo solo quando alcuni dei predecessori sono funzioni deterministiche di altri.

Possiamo mettere insieme la regola della catena e la definizione di genitori, dando

P(X1, X2,—, Xn)

=

∏i=1n P(Xi|parents(Xi)).

La probabilità su tutte le variabili, P(X1, X2,—,Xn), è chiamata distribuzione di probabilità congiunta. Una rete di credenza definisce una fattorizzazione della distribuzione di probabilità congiunta, dove le probabilità condizionali formano fattori che vengono moltiplicati insieme.

Una rete di credenza, chiamata anche rete bayesiana, è un grafo diretto aciclico (DAG), dove i nodi sono variabili casuali. C’è un arco da ogni elemento di Genitori(Xi) in Xi.Associato alla rete di credenze è un insieme di distribuzioni di probabilità condizionate – la probabilità condizionata di ogni variabile dati i suoi genitori (che include le probabilità precedenti di quelle variabili senza genitori).

Quindi, una rete di credenze consiste di

• un DAG, dove ogni nodo è etichettato da una variabile casuale;
• un dominio per ogni variabile casuale; e
• un insieme di distribuzioni di probabilità condizionata che danno P(X|parents(X)) per ogni variabile X.

Una rete di credenze è aciclica per costruzione. Il modo in cui la catena regolamentata compone la congiunzione dà l’ordine. Una variabile può avere solo i predecessori come genitori.Diverse decomposizioni possono risultare in diverse reti di credenza.

Esempio 6.10: Supponiamo di voler usare l’assistente diagnostico per diagnosticare se c’è un incendio in un edificio basato su informazioni rumorose dei sensori e spiegazioni possibilmente contrastanti di ciò che potrebbe essere in corso. L’agente riceve un rapporto sul fatto che tutti stiano lasciando l’edificio. Supponiamo che il sensore di segnalazione sia rumoroso: a volte segnala l’uscita quando non c’è esodo (un falso positivo), e a volte non segnala quando tutti stanno uscendo (un falso negativo). Supponiamo che l’allarme antincendio possa causare l’uscita, ma questa non è una relazione deterministica: sia la manomissione che l’incendio possono influenzare l’allarme.

Supponiamo di usare le seguenti variabili, tutte booleane, nel seguente ordine:

• La manomissione è vera quando c’è manomissione dell’allarme.
• Fire è vero quando c’è un incendio.
• Alarm è vero quando suona l’allarme.
• Smoke è vero quando c’è fumo.
• Leaving è vero se ci sono molte persone che lasciano l’edificio in una volta sola.
• Report è vero se c’è un rapporto dato da qualcuno di persone che vanno via. Report è falso se non c’è nessuna segnalazione di uscita.

La variabile Report denota la segnalazione del sensore che le persone stanno uscendo. Questa informazione è inaffidabile perché la persona che emette un tale rapporto potrebbe essere uno scherzo, o nessuno che avrebbe potuto dare un tale rapporto potrebbe essere stato attento. Questa variabile è introdotta per permettere il condizionamento su dati del sensore inaffidabili. L’agente sa cosa riporta il sensore, ma ha solo prove inaffidabili sulle persone che lasciano l’edificio.Come parte del dominio, assumiamo le seguenti indipendenze condizionali:

• Il fuoco è condizionatamente indipendente dalla manomissione (senza altre informazioni).
• L’allarme dipende sia dal fuoco che dalla manomissione. Cioè, non stiamo facendo alcuna ipotesi di indipendenza su come l’allarme dipenda dai suoi predecessori, dato questo ordinamento delle variabili.
• Il fumo dipende solo dal fuoco ed è condizionatamente indipendente dalla manomissione e dall’allarme, dato che c’è un incendio.
• Uscire dipende solo dall’allarme e non direttamente dal fuoco, dalla manomissione o dal fumo. Vale a dire, Leaving è condizionatamente indipendente dalle altre variabili dato Alarm.
• Report dipende solo direttamente da Leaving.

La rete di credenze della Figura 6.1 esprime queste dipendenze.

Figura 6.1: Rete di credenze per report di leaving dell’Esempio 6.10

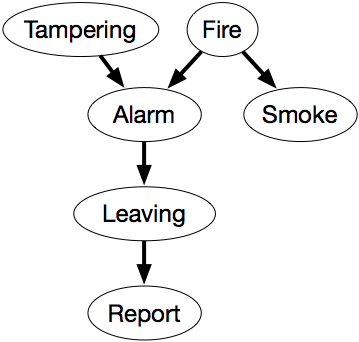
Questa rete rappresenta la fattorizzazione

P(Manomissione,Fuoco,Allarme,Fumo,Uscita,Report)
	=	P(manomissione) ×P(incendio) ×P(allarme|manomissione,incendio)
		×P(fumo|incendio) ×P(uscita|allarme) ×P(report|uscita).

Dobbiamo anche definire il dominio di ogni variabile. Assumiamo che le variabili siano booleane; cioè, hanno il dominio {vero,falso}. Usiamo la variante minuscola della variabile per rappresentare il valore vero e usiamo la negazione per il valore falso. Così, per esempio, Tampering=true è scritto come tampering, e Tampering=false è scritto come ¬tampering.

Gli esempi che seguono assumono le seguenti probabilità condizionali:

P(manomissione) = 0,02
P(incendio) = 0,01
P(allarme | incendio ∧manomissione) = 0.5
P(allarme | fuoco ∧¬tampering) = 0,99
P(allarme | incendio ∧tampering) = 0,85
P(allarme | incendio ∧¬tampering) = 0,0001
P(fumo | fuoco ) = 0.9
P(fumo | incendio ) = 0.01
P(uscita | allarme) = 0.88
P(uscita | allarme ) = 0.001
P(rapporto | uscita ) = 0.75
P(rapporto | uscita ) = 0.01

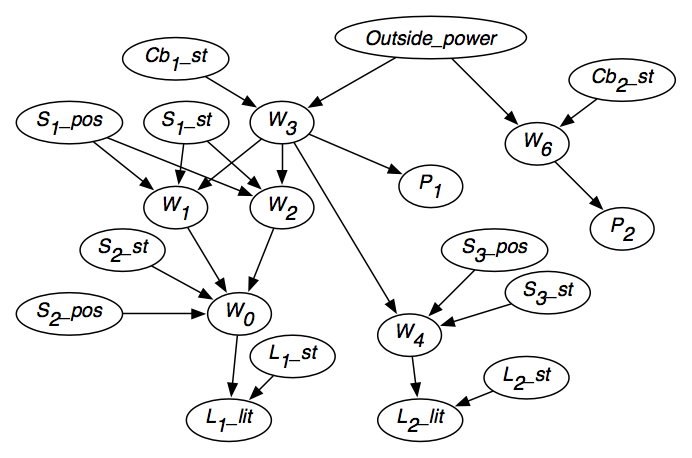
• Per ogni filo wi, c’è una variabile casuale, Wi, nel dominio {live,dead}, che indica se c’è corrente nel filo wi. Wi=live significa che il filo wi è alimentato. Wi=morto significa che non c’è corrente nel filo wi.
• Outside_power con dominio {live,dead} denota se c’è corrente che entra nell’edificio.
• Per ogni interruttore si, la variabile Si_pos denota la posizione di si. Ha il dominio {su,giù}.
• Per ogni interruttore si, la variabile Si_st denota lo stato dell’interruttore si. Ha il dominio {ok, capovolto, corto, intermittente, rotto}. Si_st=ok significa che l’interruttore si sta lavorando normalmente. Si_st=upside_down significa che l’interruttore si è installato al contrario. Si_st=short significa che l’interruttore si è accorciato e agisce come un filo. Si_st=broken significa che l’interruttore si è rotto e non permette il flusso di elettricità.
• Per ogni interruttore di circuitoercbi, la variabile Cbi_st ha il dominio {on,off}. Cbi_st=on significa che la corrente può fluire attraverso cbi e Cbi_st=off significa che la corrente non può fluire attraverso cbi.
• Per ogni luce li, la variabile Li_st con dominio {ok,intermittente,rotto} indica lo stato della luce. Li_st=ok significa che la luce li si accende se alimentata, Li_st=intermittente significa che la luce li si accende a intermittenza se alimentata, e Li_st=rotta significa che la luce li non funziona.

Una rete di credenze è una rappresentazione grafica dell’indipendenza condizionata; l’indipendenza ci permette di rappresentare gli effetti diretti all’interno del grafico e prescrive quali probabilità devono essere specificate. Le probabilità posteriori arbitrarie possono essere derivate dalla rete.

L’ipotesi di indipendenza incorporata in una rete di credenza è la seguente: ogni variabile casuale è condizionatamente indipendente dai suoi non-discendenti dati i suoi genitori. Cioè, se X è una variabile casuale con genitori Y1,…, Yn, tutte le variabili casuali che non sono discendenti diX sono condizionatamente indipendenti da X dato Y1,…, Yn:

P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),

se R non comporta un discendente di X. Per questa definizione, includiamo X come un discendente di se stesso. Il lato destro di questa equazione è la forma delle probabilità che sono specificate come parte della rete di credenze. R può coinvolgere gli antenati di X e altri nodi finché non sono discendenti di X. L’ipotesi di indipendenza afferma che tutta l’influenza delle variabili non discendenti è catturata conoscendo il valore dei genitori di X.

Spesso, ci riferiamo solo al DAG etichettato come una rete di credenze. Quando questo viene fatto, è importante ricordare che un dominio per ogni variabile e un insieme di distribuzioni di probabilità condizionali sono anche parte della rete.

Il numero di probabilità che deve essere specificato per ogni variabile è esponenziale nel numero di genitori della variabile.L’assunzione di indipendenza è utile nella misura in cui il numero di variabili che influenzano direttamente un’altra variabile è piccolo. Si dovrebbero ordinare le variabili in modo che i nodi abbiano il minor numero possibile di genitori.

Reti di credenze e causalità

Le reti di credenze sono state spesso chiamate reti causali e sono state considerate una buona rappresentazione della causalità.Ricordiamo che un modello causale predice il risultato degli interventi.Supponiamo di avere in mente un modello causale di un dominio, dove il dominio è specificato in termini di un insieme di variabili casuali. Per ogni coppia di variabili casuali X1e X2, se esiste una connessione causale diretta da X1 a X2 (cioè, intervenire per cambiare X1 in qualche contesto di altre variabili influisce su X2 e questo non può essere modellato avendo qualche variabile che interviene), aggiungete un arco daX1 a X2. Ci si aspetterebbe che il modello causale obbedisca all’ipotesi di indipendenza della rete di credenze. Così, tutte le conclusioni della rete di credenze sarebbero valide.

Ti aspetteresti anche che un tale grafico sia aciclico; non vuoi che qualcosa alla fine causi se stesso. Questa assunzione è ragionevole se si considera che le variabili casuali rappresentano eventi particolari piuttosto che tipi di eventi. Per esempio, consideriamo una catena causale secondo la quale “essere stressato” ti fa “lavorare in modo inefficiente”, che, a sua volta, ti fa “essere stressato”. Per rompere il ciclo apparente, possiamo rappresentare “essere stressati” in diverse fasi come diverse variabili casuali che si riferiscono a tempi diversi. Essere stressato in passato ti fa lavorare male in questo momento, il che ti fa essere stressato in futuro. Le variabili dovrebbero soddisfare il principio di chiarezza e avere un significato ben definito. Le variabili non dovrebbero essere viste come tipi di eventi.

La rete di credenze in sé non ha nulla da dire sulla causalità, e può rappresentare l’indipendenza non causale, ma sembra particolarmente appropriata quando c’è causalità in un dominio. L’aggiunta di archi che rappresentano la causalità locale tende a produrre una piccola rete di credenza. La rete di credenze dellaFigura 6.2 mostra come questo può essere fatto per un dominio semplice.

La rete di credenze modella gli interventi. Se qualcuno forzasse artificialmente una variabile ad avere un particolare valore, i discendenti della variabile – ma nessun altro nodo – ne sarebbero influenzati. Infine, si può vedere come la causalità nelle reti di credenza si collega al ragionamento causale e probatorio discusso nella sezione 5.7. Una rete di credenza causale può essere vista come via di assiomatizzazione in una direzione causale. Il ragionamento nelle reti di credenza corrisponde all’induzione alle cause e poi alla previsione a partire da queste. Esiste una mappatura diretta tra la visione logico-induttiva discussa nella sezione 5.7 e le reti di credenza: Le reti di credenza possono essere modellate come programmi logici con probabilità su possibili ipotesi. Questo è descritto nella sezione 14.3.

Nota la restrizione “ogni variabile casuale è condizionatamente indipendente dai suoi non discendenti dati i suoi genitori” nella definizione dell’indipendenza codificata in una rete di credenze. SeR contiene un discendente della variabile X, l’assunzione di indipendenza non è direttamente applicabile.

Una rete di credenza specifica una distribuzione congiunta di probabilità dalla quale possono essere derivate probabilità condizionali arbitrarie. Una rete può essere interrogata chiedendo la probabilità condizionale di qualsiasi variabile condizionata dai valori di qualsiasi altra variabile. Questo è tipicamente fatto fornendo osservazioni su alcune variabili e interrogando un’altra variabile.

• 6.3.1 Costruzione di reti di credenza