Nella Guerra dei Mondi, giganteschi robot alieni emergono dal terreno e cominciano a vaporizzare un gran numero di attori. C’è molto da apprezzare in quelle scene, ma ci sono tre cose che non potevo sopportare.
Come quelle tre gambe su cui camminavano. Non la loro fragilità, ma la loro effettiva tridimensionalità.

Per favore prendi Tom Cruise prima, per favore prendi Tom Cruise prima, per favore prendi …
Ci dovrebbero essere più gambe. Circa sei, in particolare.
“Guarda,” si potrebbe rispondere, “è una nave aliena, e chissà che tipo di principi hanno scoperto.”
Certo, è possibile. Ma un altro modo di vedere la cosa è che noi terrestri abbiamo una grande varietà di piani del corpo e degli arti, eppure non troviamo il design a tre arti da nessuna parte. Forse questo è un buon argomento che gli alieni non costruirebbero una nave con tre gambe.
Come facciamo noi terrestri per il design degli arti?
Tendiamo a seguire una legge, una legge che può attraversare tutti i phyla animali, una legge che ho pubblicato per la prima volta nel Journal of Theoretical Biology nel 2001, ed elaborato nel mio primo libro The Brain from 25,000 Feet .

Questa “legge degli arti” mette in relazione il numero di arti di un animale con la lunghezza di questi arti (rispetto alle dimensioni del corpo).
Quando gli arti di un animale sono molto lunghi rispetto alle dimensioni del corpo, ho sostenuto che la soluzione ottimale per raggiungere l’esterno (che utilizza la minor quantità di “filo” o materiale degli arti) è di avere circa sei arti. (Questo vale per gli animali con arti che sono approssimativamente diretti radialmente intorno ad un perimetro. Per gli animali le cui direzioni degli arti sono uniformemente distribuite su una superficie sferica, il numero previsto di arti in questo caso sarebbe circa 12.)

Come gli arti dell’animale si accorciano rispetto alle dimensioni del corpo, il numero previsto di arti aumenta, con un numero enorme di arti quando gli arti sono molto corti. (A proposito, un serpente è coerente con un numero infinito di arti infinitamente corti – cioè, nessun arto.)
Più in generale, la legge predice che il numero di arti di un animale è inversamente proporzionale alla lunghezza relativa degli arti. E, più specificamente, la legge predice una particolare costante di proporzionalità, così che “sei” è la soluzione nel caso di arti molto lunghi.
Lasciando che L sia la lunghezza dell’arto e R il raggio del corpo dell’animale, allora k = L / (L + R) è la lunghezza relativa dell’arto, o “rapporto degli arti”.
Il numero di arti, N, dovrebbe variare approssimativamente come

N ≈ 2π/k ≈6.28 k-1
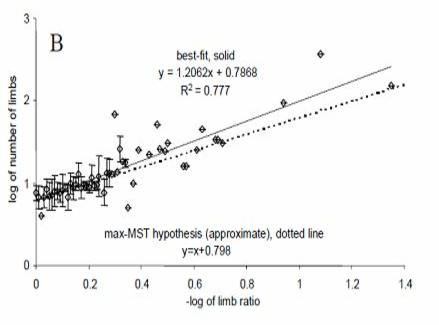
La figura qui sotto (tratta dal mio primo libro) mostra come il numero di arti sia in effetti legato al rapporto tra gli arti, per 190 specie di sette phyla animali (Annelida, Arthropoda, Cnidaria, Echinodermata, Mollusca, Vertebrata, e Tardigrada).

La tendenza prevista è mostrata con la linea continua, coerente con l’equazione N ≈ 6.28k-1 che abbiamo visto poco sopra.

La tendenza reale è mostrata con la linea tratteggiata, che porta a un’equazione empirica di N ≈6.24k-1.17 … o molto vicino alla previsione.
Per avere una migliore impressione della legge degli arti che i terrestri sembrano seguire, guardate questo piccolo programma visivo dinamico di Eric Bolz, che vi permette di variare la lunghezza degli arti e osservare come varia il numero di arti: http://www.changizi.com/limb.html L’asse verticale destro permette di modulare il rapporto tra gli arti e di osservare come cambia il numero di arti. L’asse inferiore permette di fare creature più lunghe o più corte. L’asse verticale sinistro permette solo di ridimensionare la creatura sulla pagina.
Le navi aliene della Guerra dei Mondi dovrebbero avere – data la lunghezza dei loro arti e supponendo che debbano essere trattati come se puntassero approssimativamente su un perimetro – circa sei arti. Non tre.
Ecco perché sembrano così stupide. Sono al di fuori dello sweet spot nello spazio di progettazione degli arti.

Nel mio prossimo pezzo, discuterò come questa idea degli arti ci dice perché abbiamo 10 dita, e forse, quindi, perché abbiamo un sistema numerico in base 10.