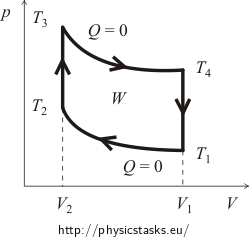
Al principio, di solito è necessario farsi un’idea del diagramma pV del ciclo. Per questo tracceremo le curve dei processi isocorici e adiabatici. Il grafico approssimativo del ciclo Otto è mostrato nella figura seguente.
L’efficienza η del ciclo è definita come
\
dove W è il lavoro compiuto dal gas durante un ciclo meno il lavoro compiuto dalle forze esterne (nel diagramma è rappresentato dalla superficie dell’area definita dalle linee del ciclo!) e Qsup è il calore fornito al sistema durante il ciclo.
Il lavoro W può essere calcolato usando la relazione tra la pressione e il volume durante un’espansione e una compressione adiabatica (il lavoro compiuto durante un processo isocorico è ovviamente zero). In questo compito, tuttavia, sarà meglio utilizzare il fatto che la variazione totale dell’energia interna per ciclo deve essere uguale a zero (si ritorna allo stesso stato di partenza, quindi la temperatura e quindi l’energia interna rimangono le stesse!) Secondo la prima legge della termodinamica, il lavoro compiuto dal gas può essere espresso come la differenza tra il calore Qsup fornito e il calore Qrel rilasciato. La formula per l’efficienza del ciclo è quindi in forma di
\8942>Primo, calcoleremo il calore fornito Qsup. È chiaro che durante il processo adiabatico non c’è scambio di calore e durante il raffreddamento isocorico il calore viene rilasciato. Ciò significa che il calore sarà fornito solo durante il riscaldamento isocorico dalla temperatura T2 alla temperatura T3. La quantità di questo calore può essere espressa nelle variabili della quantità di sostanza n del gas e della sua capacità termica molare CV come segue: \
Esprimeremo la quantità di calore rilasciato Qrel in modo molto simile. Sappiamo già che il calore viene rilasciato solo durante il raffreddamento isocorico dalla temperatura T4 alla temperatura iniziale T1. È vero che:
\
Ora sostituiamo queste formule nella formula dell’efficienza del ciclo e otteniamo immediatamente:
\
Ora dovremo esprimere le differenze di temperatura usando il rapporto di compressione dato
\8942>e il rapporto di Poisson κ.
Per fare ciò, useremo l’equazione per un gas ideale sottoposto a un processo adiabatico (la legge di Poisson) pVκ = C = konst, dove C è una costante. Ora valutiamo la pressione dall’equazione di stato di un gas ideale
che sostituiamo nella legge di Poisson. Ora trasferiamo le costanti (C e K) su un lato
\8942>Ora applichiamo questa legge di Poisson per entrambi i processi adiabatici. Per l’espansione adiabatica otteniamo la relazione \
E per la compressione adiabatica otteniamo
\
Ora sottraiamo la seconda equazione dalla prima e fattorizziamo V1κ – 1 da una parte e V2κ – 1 dall’altra. Otteniamo:
\ \
Vediamo che siamo effettivamente riusciti ad esprimere le differenze di temperatura utilizzando i valori dati. Ora sostituiamo questa relazione nella formula dell’efficienza e otteniamo l’equazione finale:
\ \