Il flusso StatsTest: Predizione >>Variabile dipendente continua >> Più di una variabile indipendente >> Nessuna misura ripetuta >> Una variabile dipendente

Non sei sicuro che questo sia il metodo statistico giusto? Usa il flusso di lavoro Choose Your StatsTest per selezionare il metodo giusto.

Che cos’è la regressione lineare multipla multivariata?

La regressione lineare multipla multivariata è un test statistico usato per prevedere più variabili di risultato usando una o più altre variabili. Si usa anche per determinare la relazione numerica tra questi insiemi di variabili e le altre. La variabile che vuoi predire dovrebbe essere continua e i tuoi dati dovrebbero soddisfare le altre ipotesi elencate sotto.

Assunzioni per la Regressione Lineare Multipla Multivariata

Ogni metodo statistico ha delle ipotesi. Le assunzioni significano che i tuoi dati devono soddisfare certe proprietà affinché i risultati del metodo statistico siano accurati.

Le assunzioni per la Regressione Lineare Multipla Multivariata includono:

1. Linearità
2. Nessun outlier
3. Simile diffusione attraverso l’intervallo
4. Normalità dei residui
5. Nessuna multicollinearità

Tuffiamoci in ciascuna di queste separatamente.

Linearità

Le variabili che vi interessano devono essere correlate linearmente. Questo significa che se tracciate le variabili, sarete in grado di disegnare una linea retta che si adatti alla forma dei dati.

Nessun outlier

Le variabili che vi interessano non devono contenere outlier. La regressione lineare è sensibile agli outlier, o ai punti di dati che hanno valori insolitamente grandi o piccoli. Puoi dire se le tue variabili hanno degli outliers tracciandole e osservando se qualche punto è lontano da tutti gli altri punti.

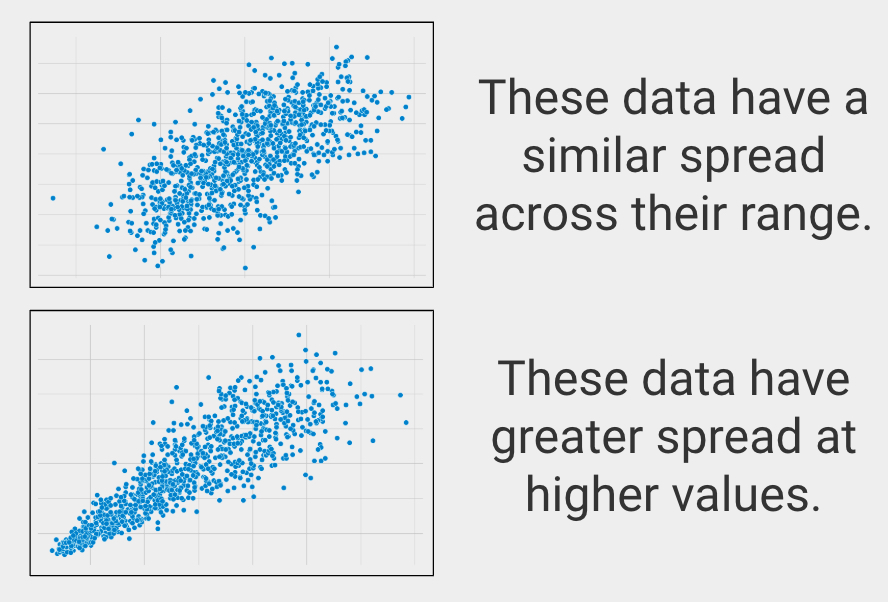
Simile diffusione nell’intervallo

In statistica questo è chiamato omoscedasticità, che descrive quando le variabili hanno una diffusione simile nei loro intervalli.

Normalità dei residui

La parola “residui” si riferisce ai valori risultanti dalla sottrazione delle variabili dipendenti attese (o previste) dai valori reali. La distribuzione di questi valori dovrebbe corrispondere a una forma di distribuzione normale (o curva a campana).

Soddisfare questo presupposto assicura che i risultati della regressione siano ugualmente applicabili in tutta la gamma dei dati e che non ci siano distorsioni sistematiche nella previsione.

Nessuna multicollinearità

La multicollinearità si riferisce allo scenario quando due o più delle variabili indipendenti sono sostanzialmente correlate tra loro. Quando la multicollinearità è presente, i coefficienti di regressione e la significatività statistica diventano instabili e meno affidabili, anche se non influisce su quanto bene il modello si adatti ai dati in sé.

Quando usare la regressione lineare multipla multivariata?

Si dovrebbe usare la regressione lineare multipla multivariata nel seguente scenario:

1. Vuoi usare una variabile in una previsione di molteplici altre variabili, o vuoi quantificare la relazione numerica tra di esse
2. Le variabili che vuoi prevedere (la tua variabile dipendente) sono continue
3. Hai più di una variabile indipendente, o una variabile che stai usando come predittore
4. Non hai misure ripetute dalla stessa unità di osservazione
5. Hai più di una variabile dipendente

Chiariamo queste cose per aiutarti a sapere quando usare la regressione lineare multipla multivariata.

Previsione

Stai cercando un test statistico per prevedere una variabile tramite un’altra. Questa è una domanda di predizione. Altri tipi di analisi includono l’esame della forza della relazione tra due variabili (correlazione) o l’esame delle differenze tra gruppi (differenza).

Variabile dipendente continua

La variabile che vuoi predire deve essere continua. Continuo significa che la vostra variabile di interesse può fondamentalmente assumere qualsiasi valore, come la frequenza cardiaca, l’altezza, il peso, il numero di barrette di gelato che potete mangiare in 1 minuto, ecc.

Tipi di dati che NON sono continui includono dati ordinati (come il posto finale in una gara, la migliore classifica aziendale, ecc), dati categorici (sesso, colore degli occhi, razza, ecc), o dati binari (acquistato il prodotto o no, ha la malattia o no, ecc).

Se la vostra variabile dipendente è binaria, dovreste usare la Regressione Logistica Multipla, e se la vostra variabile dipendente è categorica, allora dovreste usare la Regressione Logistica Multinomiale o l’Analisi Discriminante Lineare.

Più di una variabile indipendente

La regressione lineare multipla multivariata è usata quando c’è una o più variabili predittive con valori multipli per ogni unità di osservazione.

Nessuna misura ripetuta

Questo metodo è adatto allo scenario quando c’è solo una osservazione per ogni unità di osservazione. L’unità di osservazione è ciò che compone un “punto di dati”, per esempio, un negozio, un cliente, una città, ecc…

Se avete una o più variabili indipendenti ma sono misurate per lo stesso gruppo in più punti nel tempo, allora dovreste usare un modello a effetti misti.

Più di una variabile dipendente

Per eseguire la Regressione Lineare Multipla Multivariata, dovresti avere più di una variabile dipendente, o variabile che stai cercando di predire.

Se stai predicendo solo una variabile, dovresti usare la Regressione Lineare Multipla.

Esempio di Regressione Lineare Multipla Multivariata

Variabile Dipendente 1: Entrate
Variabile dipendente 2: Traffico clienti
Variabile indipendente 1: Dollari spesi in pubblicità per città
Variabile indipendente 2: Popolazione della città

L’ipotesi nulla, che è il gergo statistico per ciò che accadrebbe se il trattamento non facesse nulla, è che non ci sia alcuna relazione tra la spesa in pubblicità e i dollari pubblicitari o la popolazione per città. Il nostro test valuterà la probabilità che questa ipotesi sia vera.

Raccogliamo i nostri dati e dopo aver assicurato che i presupposti della regressione lineare sono soddisfatti, eseguiamo l’analisi.

Questa analisi esegue effettivamente la regressione lineare multipla due volte utilizzando entrambe le variabili dipendenti. Così, quando eseguiamo questa analisi, otteniamo i coefficienti beta e i valori p per ogni termine nel modello “entrate” e nel modello “traffico clienti”. Per qualsiasi modello di regressione lineare, avrete un coefficiente beta che è uguale all’intercetta della vostra linea di regressione lineare (spesso etichettata con uno 0 come β0). Questo è semplicemente il punto in cui la linea di regressione attraversa l’asse delle ordinate se si dovessero tracciare i dati. Nel caso della regressione lineare multipla, ci sono inoltre altri due coefficienti beta (β1, β2, ecc.), che rappresentano la relazione tra le variabili indipendenti e dipendenti.

Questi coefficienti beta aggiuntivi sono la chiave per capire la relazione numerica tra le vostre variabili. Essenzialmente, per ogni aumento unitario (valore di 1) di una data variabile indipendente, ci si aspetta che la vostra variabile dipendente cambi del valore del coefficiente beta associato a quella variabile indipendente (mantenendo costanti le altre variabili indipendenti).

Il p-value associato a questi valori beta aggiuntivi è la possibilità di vedere i nostri risultati assumendo che non ci sia effettivamente alcuna relazione tra quella variabile e le entrate. Un p-value inferiore o uguale a 0,05 significa che il nostro risultato è statisticamente significativo e possiamo confidare che la differenza non sia dovuta solo al caso. Per ottenere un p-value complessivo per il modello e i p-value individuali che rappresentano gli effetti delle variabili nei due modelli, si usano spesso le MANOVA.

Inoltre, questa analisi produrrà un valore R-Squared (R2). Questo valore può variare da 0-1 e rappresenta quanto bene la vostra linea di regressione lineare si adatta ai vostri punti di dati. Più alto è l’R2, meglio il tuo modello si adatta ai tuoi dati.

Domande frequenti

Q: Qual è la differenza tra la regressione lineare multipla multivariata e l’esecuzione della regressione lineare multipla?
A: Sono concettualmente simili, poiché i coefficienti del modello individuale saranno gli stessi in entrambi gli scenari. Una differenza sostanziale, tuttavia, è che i test di significatività e gli intervalli di confidenza per la regressione lineare multivariata tengono conto delle variabili dipendenti multiple.

Q: Come si esegue la regressione lineare multipla multivariata in SPSS, R, SAS o STATA?
A: Questa risorsa è incentrata sull’aiuto per scegliere il metodo statistico giusto ogni volta. Ci sono molte risorse disponibili per aiutarti a capire come eseguire questo metodo con i tuoi dati:
R articolo: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/

Help!

Se ancora non riesci a capire qualcosa, sentiti libero di contattarmi.