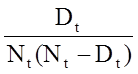Ci sono diversi modi per stimare una funzione di sopravvivenza
o una curva di sopravvivenza. Ci sono un certo numero di metodi parametrici popolari che sono usati per modellare i dati di sopravvivenza, e differiscono in termini di assunzioni che sono fatte sulla distribuzione dei tempi di sopravvivenza nella popolazione. Alcune distribuzioni popolari includono le distribuzioni esponenziale, Weibull, Gompertz e log-normale.2 Forse la più popolare è la distribuzione esponenziale, che presuppone che la probabilità di un partecipante di subire l’evento di interesse sia indipendente da quanto tempo la persona è stata senza eventi. Altre distribuzioni fanno diverse ipotesi sulla probabilità che un individuo sviluppi un evento (cioè, può aumentare, diminuire o cambiare nel tempo). Maggiori dettagli sui metodi parametrici per l’analisi della sopravvivenza possono essere trovati in Hosmer e Lemeshow e Lee e Wang1,3.
Qui ci concentriamo su due metodi non parametrici, che non fanno ipotesi su come la probabilità che una persona sviluppi l’evento cambia nel tempo. Usando i metodi non parametrici, stimiamo e tracciamo la distribuzione di sopravvivenza o la curva di sopravvivenza. Le curve di sopravvivenza sono spesso tracciate come funzioni a gradini, come mostrato nella figura sottostante. Il tempo è mostrato sull’asse X e la sopravvivenza (percentuale di persone a rischio) è mostrata sull’asse Y. Si noti che la percentuale di partecipanti che sopravvivono non sempre rappresenta la percentuale che sono vivi (il che presuppone che l’esito di interesse sia la morte). “Sopravvivenza” può anche riferirsi alla proporzione che sono liberi da un altro evento di risultato (ad esempio, la percentuale libera di MI o malattia cardiovascolare), o può anche rappresentare la percentuale che non sperimenta un risultato sano (ad esempio, la remissione del cancro).
Funzione di sopravvivenza
Nota che la probabilità di sopravvivenza è del 100% per 2 anni e poi scende al 90%. La sopravvivenza mediana è di 9 anni (cioè, il 50% della popolazione sopravvive 9 anni; vedi linee tratteggiate).
Esempio:
Considera un piccolo studio di coorte prospettico progettato per studiare il tempo alla morte. Lo studio coinvolge 20 partecipanti che hanno 65 anni e più; sono arruolati per un periodo di 5 anni e sono seguiti per un massimo di 24 anni fino a quando muoiono, lo studio termina, o abbandonano lo studio (perso al follow-up). I dati sono mostrati qui sotto. Nello studio, ci sono 6 morti e 3 partecipanti con un follow-up completo (cioè, 24 anni). I restanti 11 hanno meno di 24 anni di follow-up a causa dell’iscrizione tardiva o della perdita al follow-up.
|
Numero di identificazione del partecipante |
Anno della morte |
Anno dell’ultimo contatto |
|---|---|---|
|
1 |
|
24 |
|
2 |
3 |
|
|
3 |
|
11 |
|
4 |
|
19 |
|
5 |
|
24 |
|
6 |
|
13 |
|
7 |
14 |
|
|
8 |
|
2 |
|
9 |
|
18 |
|
10 |
|
17 |
|
11 |
|
24 |
|
12 |
|
21 |
|
13 |
|
12 |
|
14 |
1 |
|
|
15 |
|
10 |
|
16 |
23 |
|
|
17 |
|
6 |
|
18 |
5 |
|
|
19 |
|
9 |
|
20 |
17 |
|
Tabella di vita (Tabella attuariale)
Un modo per riassumere le esperienze dei partecipanti è una tabella di vita, o una tabella attuariale. Le tabelle di vita sono spesso usate nell’industria assicurativa per stimare l’aspettativa di vita e per fissare i premi. Noi ci concentriamo su un particolare tipo di tabella di vita utilizzata ampiamente nell’analisi biostatistica, chiamata tabella di vita di coorte o tabella di vita di follow-up. La tabella di vita di follow-up riassume le esperienze dei partecipanti in un periodo di follow-up predefinito in uno studio di coorte o in uno studio clinico fino al momento dell’evento di interesse o fino alla fine dello studio, a seconda di quello che si verifica per primo.
Per costruire una tabella di vita, prima organizziamo i tempi di follow-up in intervalli equamente distanziati. Nella tabella sopra abbiamo un follow-up massimo di 24 anni, e consideriamo intervalli di 5 anni (0-4, 5-9, 10-14, 15-19 e 20-24 anni). Sommiamo il numero di partecipanti che sono vivi all’inizio di ogni intervallo, il numero che muore e il numero che viene censurato in ogni intervallo.
|
Intervallo in anni |
Numero vivo all’inizio dell’intervallo |
Numero di morti durante l’intervallo |
Numero censurato |
|---|---|---|---|
|
0-4 |
20 |
2 |
1 |
|
5-9 |
17 |
1 |
2 |
|
10-14 |
14 |
1 |
4 |
|
15-19 |
9 |
1 |
3 |
|
20-24 |
5 |
1 |
4 |
Utilizziamo la seguente notazione nella nostra analisi della tabella della vita. Definiamo prima la notazione e poi la usiamo per costruire la tabella di vita.
- Nt = numero di partecipanti che sono liberi da eventi e considerati a rischio durante l’intervallo t (es, in questo esempio il numero dei vivi, poiché il nostro risultato di interesse è la morte)
- Dt = numero di partecipanti che muoiono (o subiscono l’evento di interesse) durante l’intervallo t
- Ct = numero di partecipanti censurati durante l’intervallo t Nt* = il numero medio di partecipanti a rischio durante l’intervallo t
- Nt* = il numero medio di partecipanti a rischio durante l’intervallo t [Nella costruzione delle tavole di vita attuariali, si fanno spesso le seguenti ipotesi: In primo luogo, si suppone che gli eventi di interesse (ad esempio, i decessi) si verifichino alla fine dell’intervallo e che gli eventi censurati si verifichino uniformemente (o in modo uniforme) durante l’intervallo. Pertanto, viene spesso apportata una correzione a Nt per riflettere il numero medio di partecipanti a rischio durante l’intervallo, Nt*, che viene calcolato come segue: Nt* =Nt-Ct/2 (cioè, sottraiamo la metà degli eventi censurati).
- qt = proporzione che muore (o subisce un evento) durante l’intervallo t, qt = Dt/Nt*
- pt = proporzione che sopravvive (rimane libera da eventi) nell’intervallo t, pt = 1-qt
- St, la proporzione che sopravvive (o rimane libera da eventi) dopo l’intervallo t; questa è talvolta chiamata la probabilità di sopravvivenza cumulativa e viene calcolata come segue: In primo luogo, la proporzione di partecipanti che sopravvivono dopo il tempo 0 (il tempo di inizio) è definita come S0 = 1 (tutti i partecipanti vivi o liberi da eventi al tempo zero o all’inizio dello studio). La proporzione che sopravvive dopo ogni intervallo successivo è calcolata usando i principi della probabilità condizionata introdotti nel modulo sulla Probabilità. In particolare, la probabilità che un partecipante sopravviva oltre l’intervallo 1 è S1 = p1. La probabilità che un partecipante sopravviva dopo l’intervallo 2 significa che deve sopravvivere dopo l’intervallo 1 e attraverso l’intervallo 2: S2 = P(sopravvivere dopo l’intervallo 2) = P(sopravvivere attraverso l’intervallo 2)*P(sopravvivere dopo l’intervallo 1), o S2 = p2*S1. In generale, St+1 = pt+1*St.
Il formato della tabella della vita di follow-up è mostrato sotto.
Per il primo intervallo, 0-4 anni: Al tempo 0, l’inizio del primo intervallo (0-4 anni), ci sono 20 partecipanti vivi o a rischio. Due partecipanti muoiono nell’intervallo e 1 viene censurato. Applichiamo la correzione per il numero di partecipanti censurati durante quell’intervallo per produrre Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. I calcoli delle colonne rimanenti sono mostrati nella tabella. La probabilità che un partecipante sopravviva oltre i 4 anni, o oltre il primo intervallo (usando il limite superiore dell’intervallo per definire il tempo) è S4 = p4 = 0,897.
Per il secondo intervallo, 5-9 anni: Il numero a rischio è il numero a rischio nell’intervallo precedente (0-4 anni) meno quelli che muoiono e vengono censurati (cioè, Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). La probabilità che un partecipante sopravviva oltre i 9 anni è S9 = p9*S4 = 0,937*0,897 = 0,840.
|
Intervallo in anni |
Numero a rischio durante l’intervallo, Nt |
Numero medio a rischio durante l’intervallo, Nt* |
Numero di morti durante l’intervallo, Dt |
Lost to Follow-Up, Ct |
Proporzione di morti durante l’intervallo, qt |
Tra i soggetti a rischio, proporzione di sopravvivenza intervallo, pt |
Probabilità di sopravvivenza St |
|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
20-(1/2) = 19.5 |
2 |
1 |
2/19.5 = 0.103 |
1-0.103 = 0.897 |
1(0.897) = 0.897 |
|
5-9 |
17 |
17-(2/2) = 16.0 |
1 |
2 |
1/16 = 0.063 |
1-0.063 = 0.937 |
(0,897)(0,937)=0,840 |
La tabella completa della vita di follow-up è riportata di seguito.
|
Intervallo in anni |
Numero a rischio durante l’intervallo, Nt |
Numero medio a rischio durante l’intervallo, Nt* |
Numero di morti durante l’intervallo, Dt |
Lost to Follow-Up, Ct |
Proporzione che muore durante l’intervallo, qt |
Tra quelli a rischio, Proporzione che sopravvive Intervallo, pt |
Probabilità di sopravvivenza St |
|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
19.5 |
2 |
1 |
0.103 |
0.897 |
0.897 |
|
5-9 |
17 |
16.0 |
1 |
2 |
0.063 |
0.937 |
0.840 |
|
10-14 |
14 |
12.0 |
1 |
4 |
0.083 |
0.917 |
0.770 |
|
15-19 |
9 |
7.5 |
1 |
3 |
0.133 |
0.867 |
0.668 |
|
20-24 |
5 |
3.0 |
1 |
4 |
0.333 |
0,667 |
0,446 |
Questa tabella usa il metodo attuariale per costruire la tabella delle vite successive in cui il tempo è diviso in intervalli equamente distribuiti.
Approccio Kaplan-Meier (limite del prodotto)
Un problema con l’approccio della tabella di vita mostrato sopra è che le probabilità di sopravvivenza possono cambiare a seconda di come sono organizzati gli intervalli, in particolare con piccoli campioni. L’approccio Kaplan-Meier, chiamato anche approccio del limite del prodotto, è un approccio popolare che affronta questo problema ristimando la probabilità di sopravvivenza ogni volta che si verifica un evento.
L’uso appropriato dell’approccio Kaplan-Meier si basa sul presupposto che la censura è indipendente dalla probabilità di sviluppare l’evento di interesse e che le probabilità di sopravvivenza sono comparabili nei partecipanti che sono reclutati all’inizio e più tardi nello studio. Quando si confrontano diversi gruppi, è anche importante che queste ipotesi siano soddisfatte in ogni gruppo di confronto e che, per esempio, la censura non sia più probabile in un gruppo piuttosto che in un altro.
La tabella sottostante utilizza l’approccio Kaplan-Meier per presentare gli stessi dati che sono stati presentati sopra utilizzando l’approccio della tabella di vita. Si noti che iniziamo la tabella con Tempo=0 e Probabilità di sopravvivenza = 1. Al Tempo=0 (baseline, o l’inizio dello studio), tutti i partecipanti sono a rischio e la probabilità di sopravvivenza è 1 (o 100%). Con l’approccio Kaplan-Meier, la probabilità di sopravvivenza viene calcolata usando St+1 = St*((Nt+1-Dt+1)/Nt+1). Si noti che i calcoli che utilizzano l’approccio Kaplan-Meier sono simili a quelli che utilizzano l’approccio della tabella di vita attuariale. La differenza principale è data dagli intervalli di tempo, cioè, con l’approccio della tavola di vita attuariale consideriamo intervalli equidistanti, mentre con l’approccio Kaplan-Meier, usiamo i tempi di evento osservati e i tempi di censura. I calcoli delle probabilità di sopravvivenza sono dettagliati nelle prime righe della tabella.
Tabella di vita utilizzando l’approccio Kaplan-Meier
|
Tempo, Anni |
Numero a rischio Nt |
Numero di morti Dt |
Numero censurato Ct |
Probabilità di sopravvivenza St+1 = St*((Nt+1-Dt+1)/Nt+1) |
|---|---|---|---|---|
|
0 |
20 |
|
|
1 |
|
1 |
20 |
1 |
|
1*((20-1)/20) = 0.950 |
|
2 |
19 |
|
1 |
0.950*((19-0)/19)=0.950 |
|
3 |
18 |
1 |
|
0.950*((18-1)/18) = 0.897 |
|
5 |
17 |
1 |
|
0.897*((17-1)/17) = 0.844 |
|
6 |
16 |
|
1 |
0.844 |
|
9 |
15 |
|
1 |
0.844 |
|
10 |
14 |
|
1 |
0.844 |
|
11 |
13 |
|
1 |
0.844 |
|
12 |
12 |
|
1 |
0.844 |
|
13 |
11 |
|
1 |
0.844 |
|
14 |
10 |
1 |
|
0.760 |
|
17 |
9 |
1 |
1 |
0.676 |
|
18 |
7 |
|
1 |
0.676 |
|
19 |
6 |
|
1 |
0.676 |
|
21 |
5 |
|
1 |
0.676 |
|
23 |
4 |
1 |
|
0.507 |
|
24 |
3 |
|
3 |
0,507 |
Con grandi serie di dati, questi calcoli sono noiosi. Tuttavia, queste analisi possono essere generate da programmi di calcolo statistico come SAS. Excel può anche essere utilizzato per calcolare le probabilità di sopravvivenza una volta che i dati sono organizzati per tempi e il numero di eventi e tempi censurati sono riassunti.
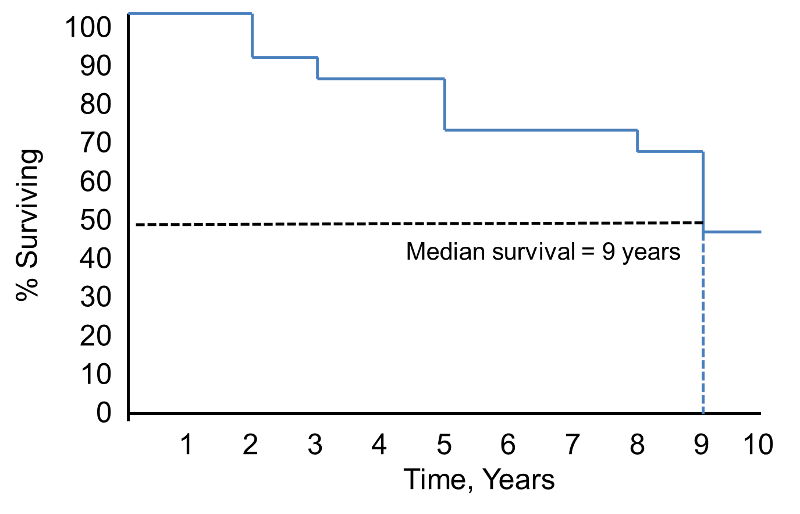
Dalla tabella di vita possiamo produrre una curva di sopravvivenza Kaplan-Meier.
Curva di sopravvivenza Kaplan-Meier per i dati di cui sopra
Nella curva di sopravvivenza mostrata sopra, i simboli rappresentano ogni tempo di evento, sia una morte che un tempo censurato. Dalla curva di sopravvivenza, possiamo anche stimare la probabilità che un partecipante sopravviva oltre i 10 anni localizzando i 10 anni sull’asse X e leggendo in alto sull’asse Y. La percentuale di partecipanti che sopravvivono oltre i 10 anni è dell’84%, e la percentuale di partecipanti che sopravvivono oltre i 20 anni è del 68%. La sopravvivenza mediana è stimata localizzando 0,5 sull’asse Y e leggendo verso l’alto e verso il basso sull’asse X. La sopravvivenza mediana è di circa 23 anni.
Errori standard e stime degli intervalli di confidenza delle probabilità di sopravvivenza
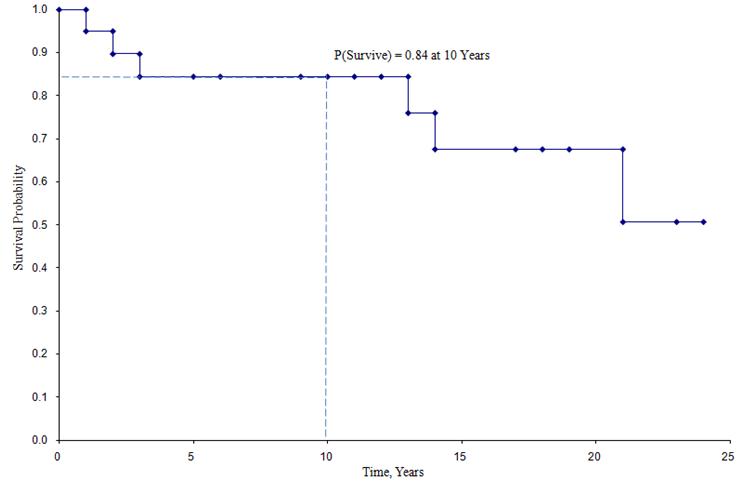
Queste stime delle probabilità di sopravvivenza in momenti specifici e il tempo mediano di sopravvivenza sono stime puntuali e devono essere interpretate come tali. Ci sono formule per produrre gli errori standard e gli intervalli di confidenza delle probabilità di sopravvivenza che possono essere generati con molti pacchetti di calcolo statistico. Una formula popolare per stimare l’errore standard delle stime di sopravvivenza è chiamata formula Greenwoods5 ed è la seguente:
La quantità 
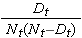è sommata per i numeri a rischio (Nt) e i numeri di morti (Dt) che si verificano attraverso il tempo di interesse (cioè, cumulativo, attraverso tutti i tempi prima del tempo di interesse, vedi esempio nella tabella sottostante). Gli errori standard sono calcolati per le stime di sopravvivenza per i dati nella tabella sottostante. Si noti che la colonna finale mostra la quantità 1,96*SE(St) che è il margine di errore e usato per calcolare le stime dell’intervallo di confidenza al 95% (cioè, St ± 1,96 x SE(St)).
Erori standard delle stime di sopravvivenza
|
Tempo, Anni |
Numero a rischio Nt |
Numero di morti Dt |
Probabilità di sopravvivenza Probabilità St |
|
|
|
1.96*SE (St) |
|---|---|---|---|---|---|---|---|
|
0 |
20 |
|
1 |
|
|
|
|
|
1 |
20 |
1 |
0.950 |
0.003 |
0.003 |
0.049 |
0.096 |
|
2 |
19 |
|
0.950 |
0.000 |
0.003 |
0.049 |
0.096 |
|
3 |
18 |
1 |
0.897 |
0.003 |
0.006 |
0.069 |
0.135 |
|
5 |
17 |
1 |
0.844 |
0.004 |
0.010 |
0.083 |
0.162 |
|
6 |
16 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
9 |
15 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
10 |
14 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
11 |
13 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
12 |
12 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
13 |
11 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
14 |
10 |
1 |
0.760 |
0.011 |
0.021 |
0.109 |
0.214 |
|
17 |
9 |
1 |
0.676 |
0.014 |
0.035 |
0.126 |
0.246 |
|
18 |
7 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
19 |
6 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
21 |
5 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
23 |
4 |
1 |
0.507 |
0.083 |
0.118 |
0.174 |
0.341 |
|
24 |
3 |
|
0.507 |
0,000 |
0,118 |
0,174 |
0,341 |
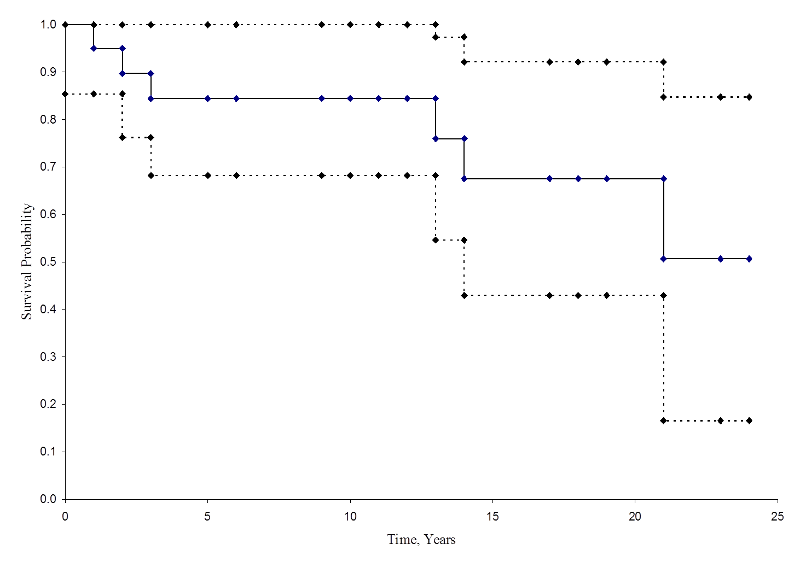
La figura seguente riassume le stime e gli intervalli di confidenza nella figura sottostante. La curva di sopravvivenza Kaplan-Meier è mostrata come una linea solida, e i limiti di confidenza al 95% sono mostrati come linee tratteggiate.
Curva di sopravvivenza Kaplan-Meier con intervalli di confidenza
Curve di incidenza cumulativa
Alcuni ricercatori preferiscono generare curve di incidenza cumulativa, al contrario delle curve di sopravvivenza che mostrano le probabilità cumulative di sperimentare l’evento di interesse. L’incidenza cumulativa, o probabilità cumulativa di fallimento, è calcolata come 1-St e può essere calcolata facilmente dalla tabella di vita usando l’approccio Kaplan-Meier. Le probabilità cumulative di fallimento per l’esempio di cui sopra sono mostrate nella tabella sottostante.
Tabella di vita con probabilità cumulative di fallimento
|
Tempo, Anni |
Numero a rischio Nt |
Numero di morti Dt |
Numero Censurato Ct |
Probabilità di sopravvivenza St |
Probabilità di fallimento 1-St |
|---|---|---|---|---|---|
|
0 |
20 |
|
1 |
0 |
|
|
1 |
20 |
1 |
|
0.950 |
0.050 |
|
2 |
19 |
|
1 |
0.950 |
0.050 |
|
3 |
18 |
1 |
|
0.897 |
0.103 |
|
5 |
17 |
1 |
|
0.844 |
0.156 |
|
6 |
16 |
|
1 |
0.844 |
0.156 |
|
9 |
15 |
|
1 |
0.844 |
0.156 |
|
10 |
14 |
|
1 |
0.844 |
0.156 |
|
11 |
13 |
|
1 |
0.844 |
0.156 |
|
12 |
12 |
|
1 |
0.844 |
0.156 |
|
13 |
11 |
|
1 |
0.844 |
0.156 |
|
14 |
10 |
1 |
|
0.760 |
0.240 |
|
17 |
9 |
1 |
1 |
0.676 |
0.324 |
|
18 |
7 |
|
1 |
0.676 |
0.324 |
|
19 |
6 |
|
1 |
0.676 |
0.324 |
|
21 |
5 |
|
1 |
0.676 |
0.324 |
|
23 |
4 |
1 |
|
0.507 |
0.493 |
|
24 |
3 |
|
3 |
0.507 |
0,493 |
La figura sottostante mostra l’incidenza cumulativa di morte per i partecipanti arruolati nello studio sopra descritto.
Curva di incidenza cumulativa
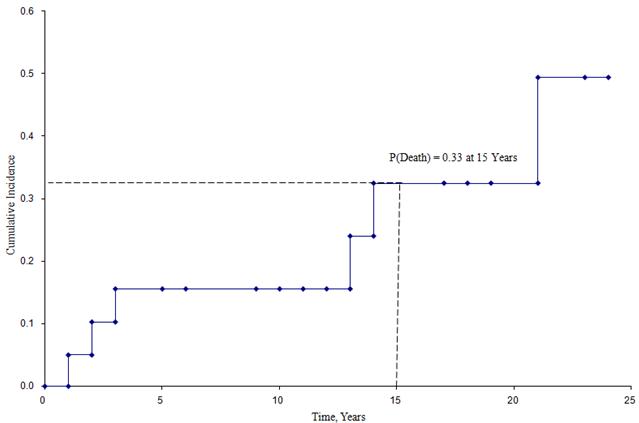
Da questa figura possiamo stimare la probabilità che un partecipante muoia entro un certo periodo di tempo. Per esempio, la probabilità di morte è di circa il 33% a 15 anni (Vedi linee tratteggiate).
Torna all’inizio | pagina precedente | pagina successiva