Test Kolmogorov-Smirnov
Il test K-S è un test di bontà dell’adattamento usato per valutare l’uniformità di un insieme di distribuzioni di dati. È stato progettato in risposta alle carenze del test del chi-quadrato, che produce risultati precisi solo per distribuzioni discrete e suddivise in fasce. Il test K-S ha il vantaggio di non fare supposizioni sulla suddivisione in fasce degli insiemi di dati da confrontare, eliminando la natura arbitraria e la perdita di informazioni che accompagna il processo di selezione delle fasce.
In statistica, il test K-S è il test accettato per misurare le differenze tra insiemi di dati continui (distribuzioni di dati senza binning) che sono una funzione di una singola variabile. Questa misura di differenza, la statistica K-S \(D\), è definita come il valore massimo della differenza assoluta tra due funzioni di distribuzione cumulative. Il test K-S unilaterale è usato per confrontare un set di dati con una funzione di distribuzione cumulativa nota, mentre il test K-S bilaterale confronta due diversi set di dati. Ogni serie di dati fornisce una diversa funzione di distribuzione cumulativa, e il suo significato risiede nella sua relazione con la distribuzione di probabilità da cui la serie di dati è tratta: la funzione di distribuzione di probabilità per una singola variabile indipendente \(x\) è una funzione che assegna una probabilità a ogni valore di \(x\). La probabilità assunta dal valore specifico \(x_{i}\ è il valore della funzione di distribuzione di probabilità a \(x_{i}\ e viene indicata con \(P(x_{i})\).La funzione di distribuzione cumulativa è definita come la funzione che dà la frazione di punti dati a sinistra di un dato valore \(x_{i}\, \(P(x <x_{i})\); essa rappresenta la probabilità che \(x\) sia minore o uguale a uno specifico valore \(x_{i}\.
Così, per confrontare due diverse funzioni di distribuzione cumulativa \(S_{N1}(x)\) e \(S_{N2}(x)\), la statistica K-S è
D = max|S_N1(x) – S_N2(x)|
dove \(S_{N}(x)\) è la funzione di distribuzione cumulativa della distribuzione di probabilità da cui è tratto un dataset con \(N) eventi. Se \(N) eventi ordinati si trovano in punti dati \(x_{i}\), dove \(i = 1, \ldots, N\), allora
S_N(x_i) = (i-N)/N
dove l’array di dati \(x\) è ordinato in ordine crescente. Questa è una funzione a gradini che aumenta di \(1/N\) al valore di ogni punto dati ordinato.
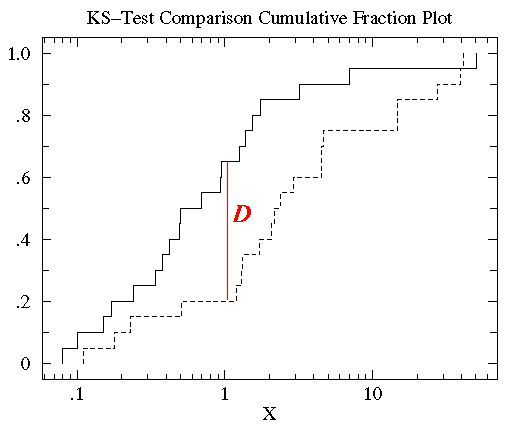
Kirkman, T.W. (1996) Statisti da usare.
http://www.physics.csbsju.edu/stats/
Per i nostri scopi, le due distribuzioni confrontate sono la distribuzione misurata dei tempi di arrivo, e la frazione accumulata sull’intervallo di tempo trascorso. Se l’ipotesi nulla (nessuna variabilità) è valida, otteniamo il 50% degli eventi nel 50% del tempo trascorso, e la statistica \(D\) dovrebbe distribuirsi secondo la distribuzione di Kolmogorov per molte realizzazioni della distribuzione dei tempi di arrivo. La probabilità restituita dal test è quindi \(p_{KS} = 1 – \alpha\), dove \(\alpha\) è la probabilità (sotto la distribuzione di Kolmogorov) che il valore di \(D\) sia maggiore o uguale al valore misurato. Un piccolo valore di \(p_{KS}\ indica quindi la coerenza con l’ipotesi nulla, mentre un grande valore di \(p_{KS}\ indica che l’intervallo tra gli eventi non è costante, e quindi la variabilità può essere dedotta.