6.3 Belief Networks
条件付き独立性の概念は、多くの領域の簡潔な表現を与えるために使用することができます。 この考え方は、ランダムな変数Xが与えられたとき、Xが直接影響する変数の値を与えられた他の変数から条件付きで独立であるという意味で、その変数の値に直接影響する変数の小さな集合が存在する可能性があるということである。 このような局所的に影響を与える変数の集合をマルコフブランケットと呼ぶ。 この局所性を利用したのが、ビリーフネットワークである。 信念ネットワークは、一組の確率変数間の条件付き依存性の有向モデルである。 信念ネットワーク(Belief Network)における条件付き独立性の正確な記述は、この方向性を考慮したものである。 次に、変数の総順序X1,…,Xnを選択する。
連鎖法則(命題6.3)は、条件付き確率に接続詞を分解する方法を示している。
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1)=X1).
あるいは、確率変数と確率分布の観点から、
P(X1, X2,—, Xn) = ∏P(Xi|X1, —, Xi-1)⊖。
確率変数Xiの親(parents(Xi))を、Xiの他の先行者がparents(Xi)を与えられたXiから条件付き独立である、全順序におけるXiの先行者の最小集合と定義する。 すなわち、parents(Xi) ⊆{X1,…,Xi-1} that
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
複数の最小集合がある場合、任意の最小集合を親として選択することが可能である。
連鎖法則と親の定義を合わせて、
P(X1, X2,—, Xn) = ∏i=1n P(Xi|parents(Xi)) とするとよい。
すべての変数に対する確率、P(X1,X2,—,Xn)を合同確率分布と呼ぶ。 ベイズネットワークとも呼ばれる信念ネットワークはacyclicdirected graph (DAG)であり、そのノードが確率変数である。 信念ネットワークに関連するのは、条件付き確率分布のセット、すなわち、その親を与えられた各変数の条件付き確率(これは親を持たないそれらの変数の事前確率を含む)である。
従って、belief network は
- a DAG, where each node is labeled by a random variable;
- a domain for each random variable; and
- a set of conditional probability distributions giving P(X|parents(X)) for each variable X.
a belief network is acyclic by construction.から構成される。 連鎖法則が接続詞を分解する方法によって順序が決定される。 異なる分解は異なる信念ネットワークになることがある。
次の変数を使用するとします。これらはすべてブール値で、次の順序で使用します:
- 改ざんはアラームに改ざんがあったときに真となります。
- Fire は火災があったときに真になります。
- Alarm は警報が鳴ったときに真になります。
- Smoke は煙があったときに真になります。
- Leaving は一度に多くの人が建物から出て行ったときに真になります。
変数Reportは、人が出て行くというセンサーの報告を表す。 この情報は信頼できない。なぜなら、そのような報告を出す人が冗談を言っている可能性もあるし、そのような報告を出せる人が誰も注意していなかった可能性もあるからである。 この変数は、信頼性のないセンサーデータに対する条件付けを可能にするために導入された。 エージェントはセンサーが何を報告するか知っているが、人が建物から出るという信頼できない証拠しか持っていない。領域の一部として、以下の条件付き独立性を仮定する:
- 火災は(他の情報がない場合)改ざんから条件付き独立。
- 離脱はアラームにのみ依存し、FireやTampering、Smokeには直接依存しない。 つまり、LeavingはAlarmがあれば他の変数から条件付きで独立する。
- Report only directly depends on Leaving.
これらの依存関係を表したのが図6.1のビリーフネットワークだ。10
このネットワークは因数分解
P(Tampering,Fire,Alarm,Smoke,Leaving.P) を表現している。Report) = P(Tampering) ×P(Fire) ×P(Alarm|Tampering,Fire)
×P(Smoke|Fire) ×P(Leave|Alarm) ×P(Report|Leaving)。
また、各変数の領域を定義しなければならない。 変数がブール値であると仮定する。すなわち、それらはドメイン{true,false}を持つ。 我々は、真の値を表すために変数の小文字の変数を使用し、偽の値には否定を使用する。 したがって、例えば、Tampering=trueはtamperingと書かれ、Tampering=falseは¬tamperingと書かれる。
この後の例では、以下の条件付き確率を仮定している:
P(fire) = 0.01
P(alarm | fire ∧tampering) = 0.01
P(alarm | fire ∧tampering) = 0.5
P(警報|火災∧¬tampering)=0.99
P(警報|¬火災∧tampering)=0.85
P(警報|¬火災∧¬tampering)=0.0001
P(煙|火災 )=0…0
P(警報|火災∧¬tampering)=0.00
P(警報|火災∧¬tampering)=1.9
P(smoke | ¬fire ) = 0.01
P(leaving | alarm) = 0.88
P(leaving | ¬alarm ) = 0.001
P(report | leaving ) = 0.75
P(report | ¬leaving ) = 0.001
P(report | ¬alarm ) = 0.01
- 各電線wiについて、電線wiに電力があるかどうかを示す領域{live,dead}の確率変数Wiが存在する。 Wi=liveはwire wiに電力があることを意味します。 Wi=deadはwire wiに電力がないことを意味する。
- Outside_powerはドメイン{live,dead}で、建物に入ってくる電力があるかどうかを示す。
- それぞれのスイッチsiに対して、変数Si_posはsiの位置を示す。 ドメインは{up,down}である。
- 各スイッチsiについて、変数Si_stはスイッチsiの状態を示す。 ドメインは{ok,upside_down,short,intermittent,broken}である。 Si_st=okはスイッチsiが正常に動作していることを意味する。 Si_st=upside_downは、スイッチsiが上下逆に設置されていることを意味する。 Si_st=shortは、スイッチsiが短絡しており、電線として動作していることを意味します。 Si_st=brokenは、スイッチsiが壊れており、電気が流れないことを意味する。
- 各回路遮断器cbiについて、変数Cbi_stはドメイン{on,off}を持つ。 Cbi_st=onはcbiに電気を流すことができることを意味し、Cbi_st=offはcbiに電気を流すことができないことを意味する。
- 各ライトliについて、ドメイン{ok,mittittro,broken}を持つ変数Li_stがライトの状態を表す。 Li_st=okは電源が入れば点灯する、Li_st=intermittentは電源が入れば断続的に点灯する、Li_st=brokenは点灯しないことを意味する。
ここで、変数の原因が変数の前にある順序を選択しよう。 例えば、照明が点灯しているかどうかの変数は、照明が動作しているかどうかと照明に電力が供給されているかどうかの変数の後に来る。
ライトl1が点灯しているかどうかは、ワイヤーw0に電力があるかどうか、ライトl1が正しく動作しているかどうかにのみ依存します。 スイッチs1の位置、ライトl2が点灯しているかどうか、カナダの女王は誰かなど、他の変数には関係ない。 したがって、L1_litの親はW0とL1_stである。
wire w0に電力があるかどうかを表す変数W0について考えてみよう。 電線w1とw2に電力があるかどうかがわかり、スイッチs2の位置とスイッチが正しく動作しているかどうかがわかれば、(L1_lit以外の)他の変数の値は電線w0に電力があるかどうかの確信に影響しないでしょう。 したがって、W0の親はS2_Pos、S2_st、W1、W2でなければならない。
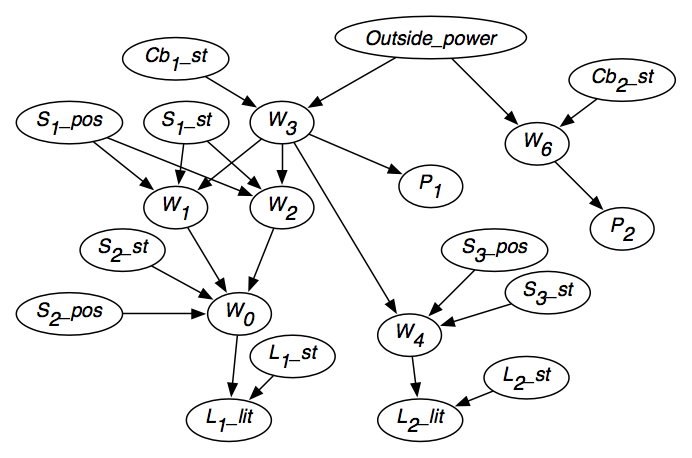
図6.2は、各変数の独立性を考慮した結果の信念ネットワークを示す。信念ネットワークには、図に示すように変数のドメインと、その親から与えられた各変数の条件付確率も含まれている。
変数W1について、以下の条件付き確率を指定する必要がある。
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live) ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
…. P(W1=live|S1_pos=down ∧S1_st=broken ∧W3=dead).
S1_posは2つ、S1_okは5つ、W3は2つあるので2×5×2=20種類のケースがW1=liveに指定しなければならないことになる。 確率論的に言えば、この20のケースのW1=liveの確率は任意に割り当てることができる。 もちろん、領域に関する知識があれば、どのような値が意味を持つかは制約される。
変数S1_stは親を持たないので、事前の分布を必要とし、それは値の1つを除く全ての確率として指定することができる。 したがって、S1_stの分布を指定するには、次の5つの確率のうち4つを指定する必要がある。
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
信念ネットワークは条件付き独立性のグラフ表現であり、独立性によってグラフ内に直接効果を描くことができ、どの確率を指定しなければならないかが規定されている。 信念ネットワークに埋め込まれた独立性の仮定は以下の通りである:各確率変数はその親を与えられた非子孫に対して条件付き独立である。 すなわち、Xが親Y1,…, Ynを持つ確率変数である場合、Xの子孫でないすべての確率変数は、Y1 ,…, Ynを与えられたXから条件付きで独立する:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
もしRにXの子孫が含まれていないなら、この定義のために、X自身を子孫として含む。 この式の右辺は、信念ネットワークの一部として指定される確率の形式である。Rは、Xの子孫でない限り、Xの祖先や他のノードを含むことができる。
しばしば、ラベル付きDAGだけを信念ネットワークと呼ぶことがある。
各変数について指定しなければならない確率の数は、その変数の親の数に対して指数関数的であり、独立性の仮定は別の変数に直接影響する変数の数が少ない限りにおいて有用である。
Belief Networks and Causality
ビリーフ・ネットワークはしばしば因果関係ネットワークと呼ばれ,因果関係の良い表現であると主張されてきた. 各確率変数X1 とX2 の組について、X1 からX2 への直接的な因果関係が存在する場合(すなわち、他の変数の文脈でX1 を変更するために介入するとX2 に影響し、これは何らかの介入変数を持っていてはモデル化できない)、X1 からX2 へ弧を追加する。 この因果モデルは、信念ネットワークの独立性の仮定に従うと予想される。 したがって、信念ネットワークの結論はすべて有効である。
また、このようなグラフが非周期的であることを期待することになる。 この仮定は、確率変数がイベントの種類ではなく、特定のイベントを表すと考えるなら、合理的である。 例えば、「ストレスを感じる」ことが「仕事の効率が悪い」ことを引き起こし、それが「ストレスを感じる」ことを引き起こすという因果関係の連鎖を考えてみよう。 この連鎖を断ち切るために、異なる段階での “ストレスを感じること “を異なる時間を参照する異なる確率変数として表現することができる。 過去にストレスを感じたことで、今現在の仕事がうまくいかず、それが原因で未来にストレスを感じるようになる。 変数は、明確性の原則と明確に定義された意味を持つshouldsatisfy。
Belief Network自体は因果関係については何も語っておらず、非因果的な独立性を表すことができるが、ドメインに因果関係がある場合に特に適しているようである。 局所的な因果関係を表す弧を追加すると、小さな信念ネットワークができあがる傾向がある。 図6.2の信念ネットワークは、これが単純なドメインでどのように行われるかを示している
Acausal Network models interventions. 誰かが人為的に特定の値を持つように変数を強制すると、その変数の子孫(他のノードには影響しない)は影響を受けるだろう。 最後に、信念ネットワークの因果関係が、5.7節で説明した因果的推論と証拠的推論にどのように関連しているかがわかるでしょう。 因果的な信念ネットワークは、因果的な方向で公理化したものと見なすことができる。 信念ネットワークにおける推論は、原因を推測し、それから予測することに相当する。 5.7節で述べた論理に基づく帰納的な見方と信念ネットワークとの間には直接的な対応関係が存在する。 信念ネットワークは、可能な仮説に対する確率を持つ論理プログラムとしてモデル化することができる。 これについては、セクション14.3で説明する。
ビリーフネットワークの独立性の定義で、「各ランダム変数はその親を与えられた非子孫から条件付きで独立である」という制約に注意。 もしRが変数Xの子孫を含んでいれば、独立性の仮定は直接適用されない。
変数S1_posには親がないため独立性の仮定は直接適用できない。 したがって、信念ネットワークに埋め込まれた独立性は、S1_posの子孫を含まない任意のAについて、P(S1_pos=up|A) =P(S1_pos=up)を指定する。
このネットワークは多くの方法で使用できる。
- スイッチと遮断器が正常であるという知識、外部電力とスイッチの位置の値を条件とすることにより、このネットワークは照明がどのように機能すべきかをシミュレートすることが可能である。
- 外部電源の値とスイッチの位置が与えられれば、ネットワークはあらゆる結果の可能性、たとえばl1が点灯する可能性を推論することができます。
- スイッチの値と照明が点灯しているかどうかが与えられると、各スイッチやブレーカーが特定の状態にある事後確率を推論できる。
- いくつかの観測結果が与えられると、ネットワークを用いて推論し、スイッチの最もありそうな位置を決定できる。
- いくつかのスイッチ位置、いくつかの出力、およびいくつかの中間値が与えられると、ネットワークを使用して、ネットワーク内の任意の他の変数の確率を決定することができる。 ネットワークは、他の変数の値を条件とする任意の変数の条件付き確率を求めることによって照会することができる。 各変数の事前確率(証拠なし)は、次のセクションの方法を使用して計算することができる。 例6.10のモデルから次の条件付き確率が小数点以下3桁まで導かれる:
P(tampering ) = 0.02
P(fire) = 0.01
P(report ) = 0.028
P(smoke) = 0.0189報告を見ると次のようになる。
P(tampering|報告) = 0.399
P(fire|report)= 0.2305
P(smoke |report) = 0.215予想通り、報告によってtamperingとfireの確率は共に増加することになる。 火災の確率が上がるので、煙の確率も上がる。
代わりに煙が観測されたとする:
P(tampering|smoke) = 0.02
P(fire|smoke) = 0.476
P(report |smoke) = 0.320煙の観測によって改竄の確率は影響を受けないが、報告と火災の確率は増加することに注意する。
仮に通報と煙の両方が観測されたとすると、
P(tampering |report ∧smoke) = 0.0284
P(fire |report ∧smoke) = 0.964両方を観測すると、火災の可能性もより高くなる。 しかし、通報の文脈では、煙の存在によって改ざんの可能性は低くなる。
代わりに、煙ではなく、報告が観測されたとする:
P(改ざん | 報告 ∧¬煙) = 0.501
P(fire|report ∧¬smoke) = 0.0294報告の文脈では、火災の可能性はかなり低くなり、報告を説明するために改竄の確率が高くなる。
この例は、信念ネットワークの独立性仮定がいかに常識的な結論を与えるかを示し、また、説明することがいかに信念ネットワークの独立性仮定の結果であるかを示している
- 6.3.1 ビリーフネットワークの構築