四面体
このページの目次
四面体とは?
四面体の断片
四面体数 |
立方体の中の四面体
四面体の輪
インターネット上の四面体 |
|
メインページ「数学バステレン」へ
四面体とは何か?
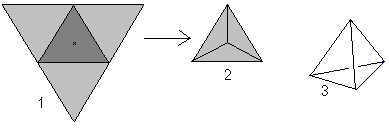
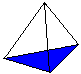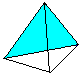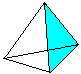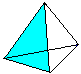
正四面体とは4つの正三角形を持つ立体図形のことです。 3つの三角形を持ち上げると(1)、上面図(2)のような正四面体になります。 一般には透視図(3)で示される。
四面体という言葉(tetrahedronは「4つの面を持つ」という意味)を見ると、三角形を底辺とするピラミッドはすべて四面体と呼ぶことができるかもしれません。
ただし、このサイトでは四面体はまっすぐな正三角形のピラミッドです。
四面体の頂点
横三角形の高さと面積
4つの正三角形は四面体を形成します
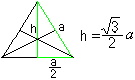 …と続きます。 …と続きます。 |
三角形を選び出す。 3つの高さが1点で交差するのは、どの三角形でも同じです。 これが三角形の中心である。 高さはピタゴラスの定理を使ってh=sqr(3)/2*aとして辺aで計算できる。 |
高さも中央値で、2:1の比率で交差している。
三角形の面積はA=sqr(3)/4*a²。
空間高
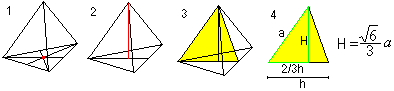
四面体の高さは基本三角形の中心(1)から頂点(2)までの間とする。 計算には、1つの辺と2つの三角形の高さで形成されるいわゆるサポートトライアングル(3, 黄色)を考慮する。 ピタゴラスの定理により、H=sqr(6)/3*a となる。
中心、外接球、内接球
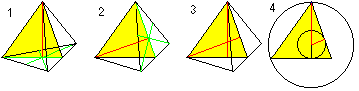
四面体の中心は二つの空間高さ(1,2,3)の交点である。 重心であり、四隅を通る球体の中心であり、四面体の中に収まる最大の球体の中心(4)でもある。
ピタゴラスの定理(1)とH=R+r(2)を用いて、rとRの2つの公式が得られます:
r=sqr(6)/12*a , R=sqr(6)/4*a があります。 |
角面
… 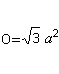 … … |
底面と側面の面積は面Oを形成している。 O=4*A(三角形)= sqr(3)a². |
Volume

Tetrahedal Numbers top
…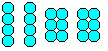 …です。 …です。 |
20個のビー玉を4個と6個で2グループに分けて接着すると、よく知られたパズルができます:4つのピースでピラミッドを形成しなければなりません。
Tetrahedron inthe cube top
6つの面の対角線は立方体の中で四面体を形成しています。
立体視ができる人は、次の2組の立方体を立体的に見ることができます。
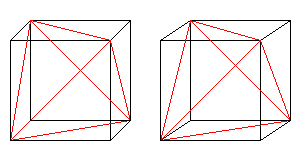 四面体の体積は立方体の体積の3分の1です。 四面体の体積は立方体の体積の3分の1です。
2番目の四面体と交線を描くと、2つの四面体の貫通図が得られます。
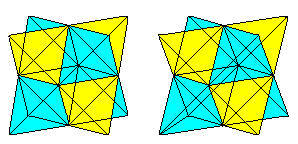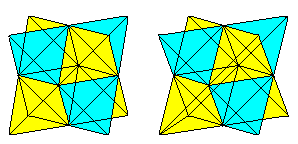
正四面体のリング 上
紙の正四面体を作り、偶数個をリングに貼り付けることができる。 リングは中心から内側に、または外側にねじれ続けることができます。 かわいいおもちゃです。 –
Tetrahedra on the Internettop
German
Christof Weber
Washat dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)
Albert Kluge
Einrotierender Tetraeder als Java-Applet
FAZ
Tetraederpackung:Eins geht noch
Georg Burkhard
Pyramidedes Cestius, Rom (u. C.)Einrotierer Tetraeder assay!
Gerd Müller
Platonische Körper in Stereodarstellung
H.A.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder
LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder
ruhr-guide
TetraederBottrop
Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode,Tetraederzahl
英語
Eric W. Weisstein (World of Mathematics)
Tetrahedron
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetrahedron
Joyce Frost and Peg Cagle (mathforum)
An amazing, space filling, non-regular Tetrahedron
Wikipedia
Tetrahedron、Tetrapod (structure)、Tetrahedralnumber
|

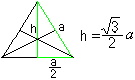 …と続きます。
…と続きます。 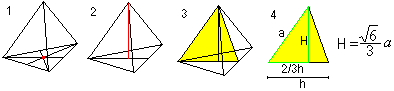
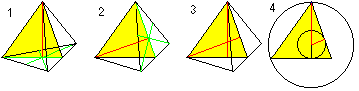

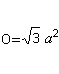 …
…
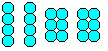 …です。
…です。
