StatsTestの流れ:予測 >>連続した従属変数 >>複数の独立変数 >>反復測定なし >>一つの従属変数
この統計手法が合っているかわからない場合は、以下のようにします。 多変量多重回帰とは何ですか。
多変量多重回帰は、1つまたは複数の他の変数を使用して、複数の結果変数を予測するために使用する統計テストです。 また、これらの変数のセットと他の変数の間の数値的な関係を決定するために使用されます。 予測したい変数は連続的でなければならず、データは以下に示す他の仮定を満たしていなければなりません。
Assumptions for Multivariate Multiple Linear Regression
どの統計手法にも仮定があります。 仮定とは、統計手法の結果が正確であるために、データがある特性を満たしていなければならないということです。
Multivariate Multiple Linear Regression の前提は次のとおりです:
- Linearity
- No Outliers
- Similar Spread across Range
- Normality of Residuals
- No Multicollinearity
これらのそれぞれを個別に見てみましょう。
線形性
気になる変数は、線形に関係していなければなりません。 これは、変数をプロットすると、データの形状に合った直線を引くことができることを意味します。
外れ値なし
気になる変数には外れ値が含まれていてはいけません。 線形回帰は、外れ値、または異常に大きい値や小さい値を持つデータポイントに敏感です。
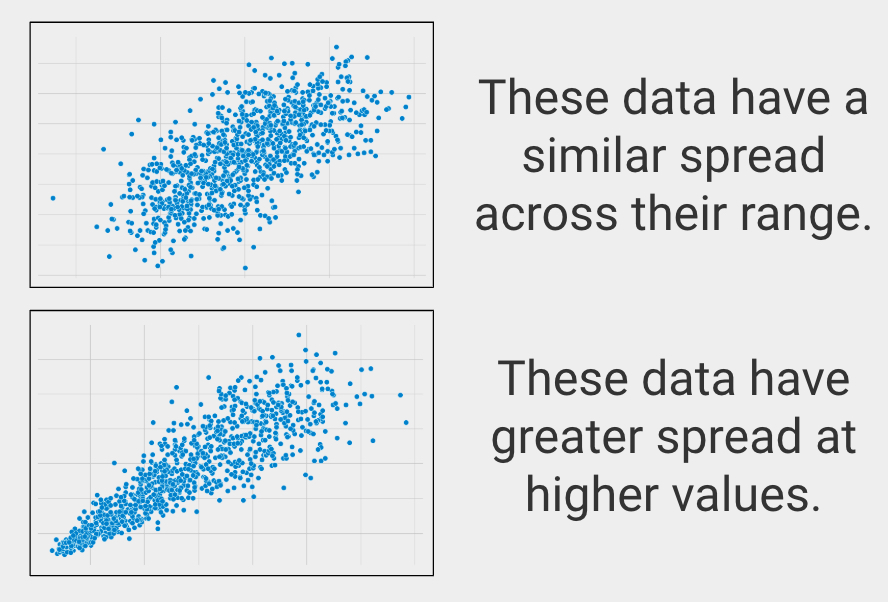
Similar Spread across Range
統計学ではこれを homoscedasticity と呼び、変数がその範囲にわたって同様の広がりを持つ場合を説明します。
残差の正規性
残差という言葉は、実際の値から期待(または予測)された従属変数を引いた結果の値を指します。 この仮定を満たすことは、回帰の結果がデータの全範囲にわたって均等に適用され、予測に系統的なバイアスがないことを保証します。 多重共線性がある場合、回帰係数や統計的有意性が不安定になり、信頼性が低下しますが、モデルがデータに適合すること自体には影響しません。
When to use Multivariate Multiple Linear Regression?
以下のシナリオでは多変量多重回帰を使用する必要があります。
- ある変数を他の複数の変数の予測に使用したい、またはそれらの間の数値関係を定量化したい
- 予測したい変数(あなたの従属変数)は連続である
- 複数の独立変数を持っている。 または予測因子として使用する1つの変数
- 同じ観測単位からの反復測定がない
- 複数の従属変数がある
これらを明らかにして、多変量多重回帰を使用するタイミングを知ることができるようにしましょう。
予測
ある変数を別の変数で予測するための統計的検定を探している。 これは予測に関する質問です。 他のタイプの分析には、2つの変数間の関係の強さを調べる(相関)、またはグループ間の差を調べる(差)などがあります。
連続従属変数
予測したい変数は連続でなければなりません。 連続的とは、心拍数、身長、体重、1 分間に食べられるアイスバーの数など、関心のある変数が基本的に任意の値を取り得ることを意味します。
連続的ではないデータの種類には、順序データ(レースでの順位、ベストビジネスランキングなど)、カテゴリデータ(性別、目の色、人種など)、バイナリデータ(製品を購入したか否か、病気を持っているかいないかなど)などが挙げられます。
従属変数がバイナリの場合はMultiple Logistic Regressionを使用し、従属変数がカテゴリの場合はMultinomial Logistic RegressionまたはLinear Discriminant Analysisを使用する必要があります。
複数の独立変数
多変量多重回帰は、観測単位ごとに複数の値を持つ1つまたは複数の予測変数がある場合に使用します。
反復測定なし
この方法は、観測単位ごとに1つの観測しかない場合のシナリオに適合します。 観測単位とは、例えば店舗、顧客、都市など「データポイント」を構成するものです。
1つ以上の独立変数があり、それらが複数の時点で同じグループに対して測定される場合、混合効果モデルを使用する必要があります。
複数の従属変数
多変量多重回帰を実行するには、複数の従属変数、または予測しようとする変数が必要です。
1つの変数だけを予測している場合は、多重回帰を使用する必要があります。
多変量多重回帰の例
従属変数 1: 収益
依存変数2:顧客アクセス
独立変数1: 都市別広告費
独立変数2:都市人口
帰無仮説とは、統計用語で「処理を何もしなければどうなるか」という意味で、「広告費と都市別広告費または人口との間には関係がない」ということである。 このテストでは、この仮説が真である可能性を評価します。
私たちはデータを収集し、線形回帰の仮定が満たされることを保証した後、分析を実行します。
この分析は、両方の従属変数を使って2回多重線形回帰を効果的に実行します。 したがって、この分析を実行すると、「収益」モデルと「顧客トラフィック」モデルの各項について、ベータ係数と p 値を得ることができます。 どのような線形回帰モデルでも、線形回帰線の切片(しばしばβ0として0が表示される)に等しい1つのベータ係数が存在します。 これは、データをプロットすると、回帰線がY軸を横切る場所です。 重回帰の場合、さらに 2 つの他のベータ係数 (ベータ 1、ベータ 2 など) があり、これらは独立変数と従属変数の間の関係を表します。 基本的に、与えられた独立変数の各単位 (1 の値) の増加に対して、従属変数はその独立変数に関連するベータ係数の値だけ変化すると期待されます (他の独立変数は一定に保ちます)。
これらの追加のベータ値に関連する p 値は、その変数と収益の間に実際に関係がないと仮定して結果を見るチャンスです。 0.05以下のp-値は、我々の結果が統計的に有意であることを意味し、その差が偶然だけによるものではないことを信頼することができます。 モデルの全体的なp値と、2つのモデルにわたる変数の効果を表す個々のp値を得るために、MANOVAがよく使われます。
さらに、この分析はR二乗(R2)値をもたらします。 この値は 0 ~ 1 の範囲で、線形回帰線がデータ ポイントにどれだけよくフィットするかを表します。
よくある質問
Q: 多変量重回帰と線形回帰を複数回実行することの違いは何ですか A: 両者は概念的に似ており、個々のモデル係数は両方のシナリオで同じになるからです。
Q: SPSS、R、SAS、またはSTATAで多変量多重回帰を実行するにはどうすればよいですか?
A: この資料は、毎回、正しい統計手法を選択することを助けることに焦点を当てています。 あなたのデータでこの方法を実行する方法を見つけ出すのに役立つ多くのリソースがあります:
Rの記事。 https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/
ヘルプ!
それでも何かわからないことがあれば、遠慮なくご連絡ください。