Kolmogorov-Smirnov Test
K-S検定はデータ分布の集合の均一性を評価するために用いられる適合度検定である。 これは、離散的でビン分けされた分布に対してのみ正確な結果を生成するカイ2乗検定の欠点に対応して設計されたものである。 K-S検定には、比較するデータセットのビン分けについて何の仮定もしないという利点があり、ビン選択のプロセスに伴う恣意性と情報の喪失を取り除くことができます。
統計学では、K-S検定は、単一の変数の関数である連続データセット(ビン化されていないデータ分布)間の差を測定するための検定として受け入れられているものです。 この差の指標であるK-S統計量は、2つの累積分布関数間の差の絶対値の最大値として定義されます。 片側 K-S 検定は、データセットと既知の累積分布関数を比較するために使用され、両側 K-S 検定は、2 つの異なるデータセットを比較するために使用されます。 データセットごとに異なる累積分布関数が得られ、その重要性はデータセットが描かれた確率分布との関係にある。単一独立変数の確率分布関数(probability distribution function for a single independent variable \(x\))は、 \(x\)の各値に確率を割り当てる関数である。 ある特定の値(x_{i})が仮定する確率は(x_{i})での確率分布関数の値であり、(P(x_{i})↘)と表記される。また、累積分布関数とは、ある値∕(x_{i}) の左側にあるデータ点の割合を与える関数で、∕(x <x_{i})\ の値がある値(x_{i}) 以下である確率を表すと定義されています。
したがって、2つの異なる累積分布関数㊧(S_{N1}(x)㊧)と㊨(S_{N2}(x)㊨)を比較するためのK-S統計量は
D = max|S_N1(x) – S_N2(x)|
ここで、㊧は、イベント㊧のデータセットから抽出した確率分布の累積分布関数のことで、Ⓒは、Ⓒのことである。 \(N) ordered events are located at data points \(x_{i}}, where \(i = 1, \ldots, N}), then
S_N(x_i) = (i-N)/N
where the \(x_) data array is sorted in increasing order.このとき、(s)は(x)データ配列が増加順に並びます。 この関数は、各順序のデータポイントの値で[(1/N)]増加するステップ関数です。
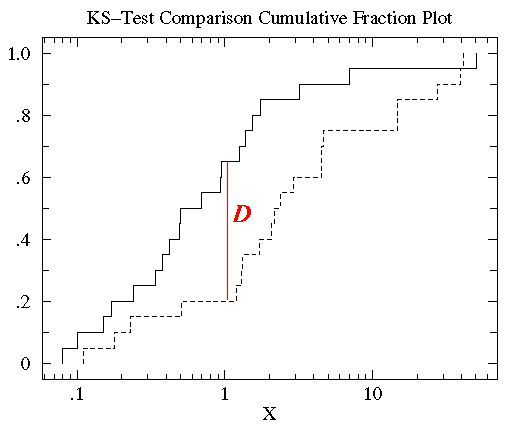
Kirkman, T.W. (1996) Statist to Use.
http://www.physics.csbsju.edu/stats/
我々の目的のために、比較する二つの分布は到着時間の測定分布と、経過した時間間隔での累積割合である。 帰無仮説(変動なし)が成立する場合、通過時間の50%で50%の事象が得られ、到着時間分布の多くの実測値に対して、 \(D) 統計量はKolmogorov分布に従うように分布するはずである。 したがって、テストが返す確率は、 \(p_{KS} = 1 – \alpha\)で、ここで、( \alpha\)は、 \(Denta) の値が測定値より大きいか等しい確率(Kolmogorov分布の下)になります。 そのため、Ⓐが小さいと帰無仮説と一致し、Ⓑが大きいと事象の間隔が一定でないため変動が推察されることを意味します。